The first part of this article appeared in The Games and Puzzles Journal, Volume 1, 1989, issues 10 and 12, pages 153 and 183 but stopped at diagram (D). The other results have been lying around unpublished ever since, partly because of difficulty in drawing diagrams accurately.
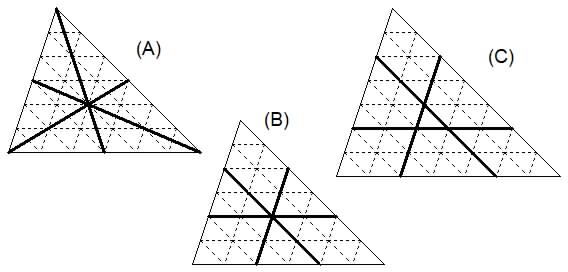
A line that passes through the centre of gravity of a shape (considered to be cut from a uniformly dense sheet of material) is called a median. The medians through the vertices of a triangle are well-known to divide it into two parts of equal area (A). The medians parallel to the sides however divide the triangle into parts whose areas are in the ratio 4 to 5 (B)
Let us call a line that divides a shape into two equal area pieces a bisector. Thus three bisectors are not necessarily concurrent. An aproximation to the position of the bisector parallel to the edge of a triangle (C) is 2/7 of the height (whereas the median is 1/3). which divides the triangle into two parts in the ratio 25 to 24. The exact value is 1 - 1/Ö2.

If we omit the centre triangle in (C) we get an array of equal triangles that can be bisected in three ways nonconcurrently into two parts each of 24 triangles. This suggests the question: Is this the smallest such arrangement of congruent pieces? The answer in No. It can be reduced to six pieces, as in (D).
If we require our cake to have no hole in the middle then the fewest pieces increases to 14, as in (E). If we further require that the two parts into which we bisect the cake shall be themselves connected pieces of cake then we need 22 pieces, as in (F). Finally, if we require that the cuts, to be proper cuts, must have cake on both sides for their whole length then we need 34 pieces, as in (G).
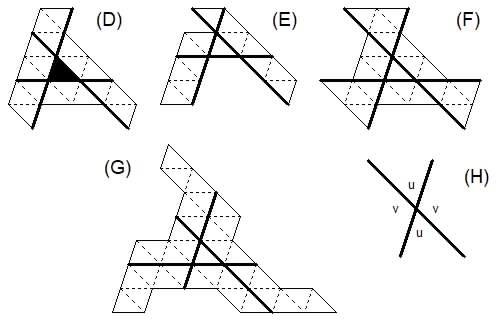
In working out these puzzles a principle to bear in mind is that when two bisectors cross (as they must) they divide the cake into four parts and 'vertically opposite' parts must contain the same number of elements (H). So if we add or remove elements in one sector we must balance them by the same number in the opposite sector.
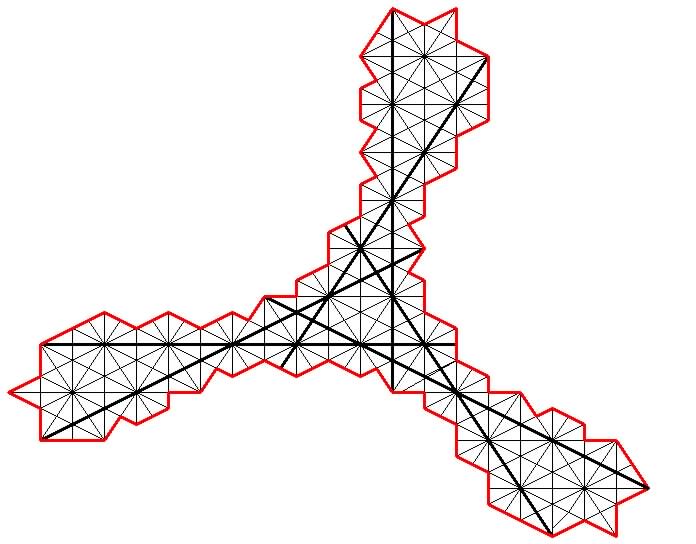
With equilateral triangular pieces we are clearly limited to three nonconcurret bisectors, but with half-square triangles we can produce four. The best solution I found was in 82 elements for the case of a connected cake and pieces and without holes. If holes are permitted then the central 10 triangles and outer areas of 1, 8, 9 and 10 triangles can be removed (in accordance with diagram H), leaving 44 elements.
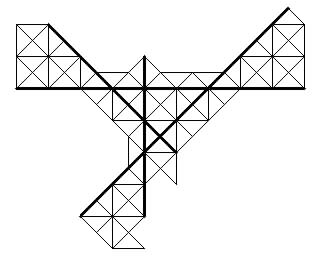
Note that in a few places the formation of the triangles has been de-regularised to allow fewer to be used to connect otherwise disconnected components. If we are obliged to keep to the regular pattern the totals of elements are 90 and 52 respectively.
With 30-60-90 triangles we can achieve five or six nonconcurrent bisectors.