Angles and Rotations
The assumption that distances in different directions can be compared enables us to define the concept of angle and the related concept of rotation. This assumption is known as the isotropy of space.
The angles round a point add up to one cycle (also termed a complete rotation or Hertz or revolution). Angles of greater than one cycle may be encountered when dealing with rotatory motion, and negative angles may arise in comparing rotations in opposite senses. By an awkward tradition, anticlockwise rotations are counted positive and clockwise negative. A cycle is traditionally divided into 360 degrees (denoted °).
A straight line through a point divides the angles there into two equal half-cycles (or hemicycles) of 180°, one on either 'side' of the line. If angles at a point add to a half-cycle then the outer arms of the figure form one straight line. Two angles adding to a half-cycle are termed supplementary. We will show that the sum of the internal angles in any triangle is a half-cycle.
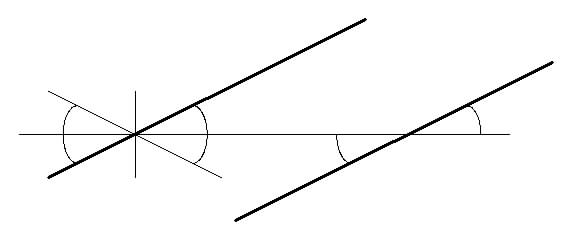
Two intersecting lines divide the plane into four angles. The 'adjacent' pairs of angles combine to form a half-plane and are supplementary. The 'vertically opposite' angles are equal.
If all four angles are equal, they are quarter-planes or quadrants. A quarter of a cycle is called a right angle of 90°. Angles that add to a right angle are called complementary. Angles less than a right angle are acute, while those greater than a right angle are obtuse. An angle between 180° and 360° is sometimes termed reflex. If two straight lines cross so that all four angles they make are equal the lines are said to be orthogonal or perpendicular (to each other).
There is a unique straight line through a given point, perpendicular to a given line. This remains true when the given point is on the given line. The perpendicular from a point to a line is the shortest line segment from the point to any point on the line and is termed the distance of the point from the line.
If a circle of radius r is drawn, then the compasses can be stepped round the circumference of the circle six times, thus dividing the cycle into six parts, called sextants of 60°. Six circular coins can be placed round one of the same type so that each touches the central coin and its two neighbours.
A line that divides a given angle into two equal parts is an angle bisector. The bisectors of the angles formed by two crossing lines are mutually perpendicular. If lines x, y make an angle A then lines x', y' perpendicular to x, y will make the same angle A.
Bisection of a right angle produces an octant, an angle of 45°. This angle is important in mechanics since it is the angle of elevation of a gun to give the greatest horizontal range for a given initial velocity.
Combining the divisions into sextants and octants we arrive at a division of the cycle into 6×4 = 8×3 = 24 which are known as hours (of arc or of rotation) of 15°. This is related to the way we traditionally measure the lapse of time, since the Earth completes one rotation in 24 hours (of time). This rotation can be measured relative to the sun or stars, and the results are slightly different.
An hour is traditionally divided into 60 minutes, and a minute into 60 seconds. This leads us to a division of the cycle into 24×60 = 1440 minutes of arc and 1440×60 = 86400 seconds of arc.
So that we can speak of the angle between any two lines in the same plane we must allow that parallel lines have a zero angle between them. Through any point there is a unique line parallel to a given line. We allow the case of a line being parallel to itself, so as to include the case when the point is on the line. Parallelism is then an equivalence relation. Lines parallel to a given line are parallel to each other. The equivalence class of all lines parallel to a given line constitutes a direction: they are all the lines 'in a given direction'.
If a line cuts two parallel lines then it makes the same corresponding angles with both. Conversely if these angles are equal the lines are parallel. The alternate angles are also equal. The angles between the parallels and the transversal are supplementary.