There is a unique (straight) line passing through any two given points. If P and Q are the points we denote the full line, extending beyond the points P and Q to the bounds of our vision, by P-Q. That part of a line between two points on it and including the two points as endpoints is called a line segment, denoted PQ. The length of the line segment PQ is the distance between the points P and Q, written d(P,Q) or just PQ when the meaning is clear. A straight line segment is the shortest path between two points.
There is a unique point common to any two straight lines that intersect. This is a consequence of the property in the previous paragraph, since if two lines met in two points there would not be a unique line between those two points. If a, b are the lines we denote the point by ab.
Two lines that do not intersect, within the bounds of our vision, are either vergent or parallel. To tell whether two lines are vergent or parallel we draw a pair of lines from a point O, not on the lines, to intersect the lines at P, P', Q, Q'. Then P-Q and P'-Q' are parallel when PQ/OQ = P'Q'/OQ' and vergent if these ratios are not equal.
If a pencil of four lines is intersected by a transversal in four points P, Q, R, S and by another transversal in P', Q', R', S', with PP', QQ', RR', SS' being collinear pairs of points, then PQ.RS/PR.QS = P'Q'.R'S'/P'R'.Q'S'. This ratio is called the cross ratio (or anharmonic ratio) and is a property of the pencil, the same for all transversals.
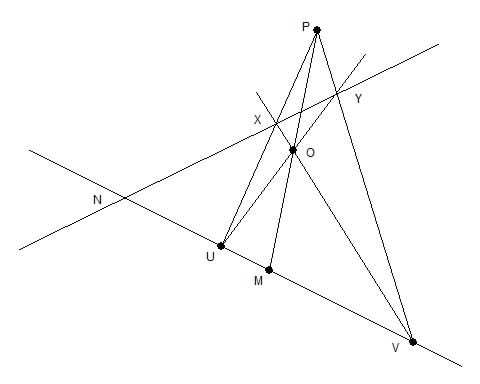
If U, V and M are three points on a line and P is any point not on the line then we can join PU, PV, PM and we can choose any point O on PM. Then the lines VO, UO will meet PU at X and PV at Y, say. Now the line XY will either be parallel to UV in which case M is the midpoint of UV or else XY and UV will be vergent or will meet at a point N. This point N is called the harmonic conjugate of M with respect to UV. In terms of distances, this means that M and N divide the length UV internally and externally in the same ratio. That is UM/MV = UN/NV.
This harmonic configuration thus provides a method of construction for the harmonic conjugate that depends only on the intersection properties of straight lines without any measurement of distances being necessary. It is a projective construction for the harmonic conjugate.
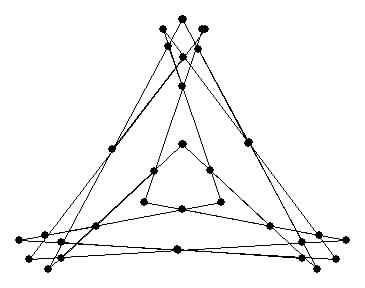
The fact that M can never be identical to N in the harmonic construction is known as Fano's Principle which is often taken as an Axiom. This means that XYM cannot be a straight line. It means, in other words that a configuration of 7 points in 7 lines with 3 points on every line and 3 lines through every point is imposssible in normal Euclidean Geometry.
An arrangement of N points in N lines with M points on each line and M lines through each point we call an orchard of type (N, M). Thus Fano tells us that an orchard of type (7, 3) is impossible. The harmonic configuration has 8 points and 7 lines.
An orchard of type (8, 3) is also impossible. The first case that is possible in Euclidean Geometry is the (9, 3) case illustrated here. This configuration illustrates the Theorem of Pappus: If there are three points (A, B, C) on one line and three corresponding points (D, E, F) on another line, then the six lines connecting pairs of non-corresponding points (AE, BD) (AF, CD) (BF, CE) intersect in pairs at points (X, Y, Z) that are collinear.
In special cases lines may be vergent or parallel instead of intersecting. For instance if AE is parallel to BD then YZ will also be parallel to these two lines. If AE||BD and BF||CE then CD||AF.
This configuration involves nine lines and nine points. Any two of the lines of three can be taken as given and then determines the other three.
The properties of lines and points with regard to intersections (or incidence) are in many respects symmetrical. This relation of symmetry is called duality. For example, two points determine a unique line passing through them and two lines determine a unique point lying on them (or are are vergent or parallel). Many theorems about points and lines remain true if dual concepts are interchanged in the statement of the theorem.
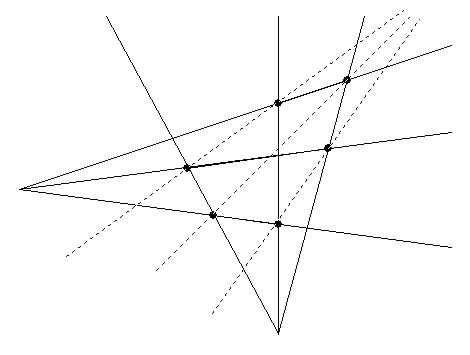
The Dual Theorem of Pappus states: If abc and def are concurrent or parallel triplets of lines then the three lines that join the pairs of intersections (ae)(bd) and (af)(cd) and (bf)(ce) also form a concurrent or parallel triplet (xyz). In other words: If two triangles are in perspective from two different points then they are in perspective from a third point.
This provides an alternative planting of a (9, 3) orchard.
The theorem disovered by Girard Desargues (1593 - 1662) and published by him in 1648 can be stated concisely as: Two triangles (or more complex figures) are in perspective from a point if and only if they are in perspective from a line. By two figures being in perspective from a point we mean that the lines (AD, BE, CF) joining corresponding points in the two figures meet at a point (O). By two figures being in perspective from a line we mean that the points (BC.EF, CA.FD, AB.DE) where corresponding lines in the two figures meet lie on the same straight line (XYZ).
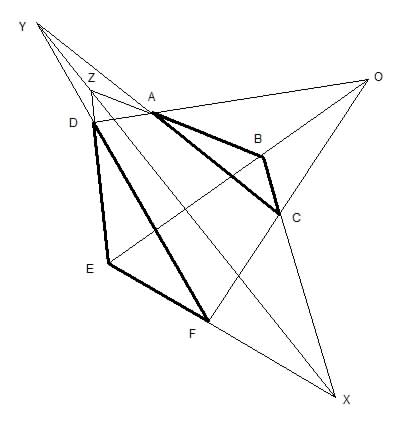
The Desargues configuration can be interpreted as a perspective drawing of a three-dimensional configuration. The lines OAD, OBE, OCF being the edges of a triangular pyramid and the triangles ABC and DEF being plane sections through the pyramid. Then the points X, Y, Z are on the line of intersection of these two planes.
This configuration involves 10 lines and 10 points in an exactly self-dual relationship.
Special cases of this configuration occur when some of the lines are parallel. When two triangles ABC and DEF are situated with sides parallel (i.e. AB||DE, BC||EF, CA||FD) then the lines joining corresponding vertices are concurrent or parallel. Conversely if two triangles are in perspective from a point or have the lines joining corresponding vertices parallel and two pairs of sides are parallel, then the third pair are also parallel. [Hilbert pp.71-71]
This is a 'condensed' version of the Desargues configuration. The vertices (A', B', C') of one of the triangles in perspective from a point (O) lie on the sides of the other triangle (A, B, C).
Given any triangle ABC and a point O not on its sides, the rest of the configuration can be constructed purely by joining points of intersection. The line XYZ is called the trilinear polar (or harmonic line) of O with respect to ABC. Conversely given the triangle ABC and any line XYZ crossing its sides the rest of the figure can be constructed. The point O is then the trilinear pole (or harmonic point) of XYZ with respect to ABC.
In this figure the harmonic construction can be seen three times. The points X, Y, Z are the harmonic conjugates of A', B', C' respectively with respect to BC, CA, AB.
The Theorem of Menelaus given by Menelaus of Alexandria (1st century AD) in his book Spherics states: If XYZ is a transversal of a triangle ABC then XA.YC.ZB = XC.YB.ZA; that is the product of three alternate segments taken cyclically is equal to the product of the other three. Conversely if the relation holds then XYZ are collinear.
The Theorem of Ceva given by Giovanni Ceva in his book De Lineis Rectis (1678) states: If lines AO, BO, CO meet the opposite edges at A', B', C' then CB'.BC'.AA' = B'B.C'A.A'C and conversely if this relation holds the three lines are concurrent.
The double-six configuration consists of 12 lines of 5 points intersecting in pairs. This pattern is also possible in three dimensions, where the marked points are then the only points of intersection.
