The Symmedian or Lemoine Centre
The reflection of a line through a vertex in the bisector of the angle at that vertex is called its isogonal line. Thus AX and AY are isogonals if BAX = CAY or BAY = CAX. The isogonals of three concurrent lines are themselves concurrent. These pairs of points are called isogonal conjugates of each other.
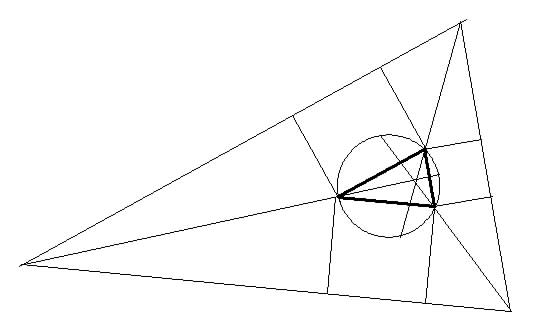
The isogonals of the medians, i.e. their reflections in the angle bisectors, are called the symmedians and they meet at the Lemoine centre, G' (the isogonal conjugate of the centroid G).
The symmedians divide the sides in the ratio of the squares of the other sides, i.e. BL' = a.c²/(c² + b²), CL' = a.b²/(c² + b²) etc BL'/CL' = c²/b².
The distances of G' from the sides are in the ratio of the sides, a:b:c. The Lemoine point G' is the point at which the areal coordinates are such that p² + q² + r² is minimum. Thus G' is the centre of mass of masses a², b², c², at A, B, C. The areas BG'C, CG'A, AG'B are in the ratios a²:b²:c².
The triangle P'Q'R' where the symmedians meet the circumcircle has the same symmedians as ABC.
If squares are drawn outwards on the sides of a triangle and the outer sides of the squares are extended to form a triangle the centre of homothecy of the two triangles is the Lemoine centre of each of them. Conversely we can start with the outer triangle and construct the inner.