Solutions to the Puzzle Issue. The response was very disappointing. Only two solvers sent in a significant number of solutions, so I decided to award each of them the prize of volumes 1 and 2 of the Journal. They are Jean-Charles Meyrignac (France) and Gabriele Carelli (Italy). In future we will keep the puzzles simpler and allow more time.

In these puzzles it is assumed that the coins available have cent values 1, 2, 5, 10, 20, 50, and 100.
56(A). Alicia has twice as much money as Bella; Bella has twice as much as Celia; Celia has twice as much as Delia. Each has two coins. Which coins does each of them hold?
56(B). Alicia, Bella, Celia, Delia, and Ella each have the same amount of money, but Alicia has one coin, Bella has two, Celia has three, Delia has four, and Ella has five. Which coins does each of them hold?
56(C). Alicia has three times as much money as Bella; Bella has three times as much as Celia. Each has three coins. Which coins does each of them hold?

SOLUTIONS
56(A). Delia has 10 + 5 = 15; Celia has 20 + 10 = 30; Bella has 50 + 10 = 60; Alicia has 100 + 20 = 120.
56(B). Each has 20 cents.
Alicia has 20; Bella has 10 + 10; Celia has 10 + 5 + 5; Delia has 5 + 5 + 5 + 5; Ella has 10 + 5 + 2 + 2 + 1.
56(C). This has three solutions, but they are quite different and each of them is precise.
Either Celia has 1 + 1 + 1 = 3, Bella has 5 + 2 + 2 = 9, Alicia has 20 + 5 + 2 = 27
or Celia has 2 + 2 + 1 = 5, Bella has 5 + 5 + 5 = 15, Alicia has 20 + 20 + 5 = 45
or Celia has 5 + 2 + 1 = 8, Bella has 20 + 2 + 2 = 24, Alicia has 50 + 20 + 2 = 72.

COMMENTS
The composer notes: The solution of 56(A) remains unique with contemporary British coinage (1, 2, 5, 10, 20, 50, 100, 200), but 56(B) admits "200 cents" as an alternative solution; in 56(C) the problem doesn't work with present British coinage: there are three more solutions, 25/75/225, 30/90/270, 50/150/450, and the second of them is dualized (30 = 10 + 10 + 10 = 20 + 5 + 5). Jean-Charles Meyrignac notes: I also tried to find some extensions, and found the following relations: (a) all values of the form 0 + 5k with k = 0 to 36 can be decomposed as sums of exactly 4 coins. (b) all values of the form 5 + k with k = 0 to 82 can be decomposed as sums of exactly 5 coins.

Find the shortest path for a bishop to visit all the black cells on (A) an 8 by 8 and (B) a 10 by 10 board, for the following cases: (a) minimise number of bishop moves, (b) minimise distance travelled by the bishop, (c) minimise number of moves times distance, (d) minimise number of moves when 'visiting' a cell means either stopping there or passing through it twice. In each case we require that the bishop completes each straight section of the path before turning, and that there be only one route along the path under this condition.

SOLUTIONS (A)
57(Aa) Solution by Siep Korteling. 11 - 88 - 77 - 86 - 31 - 13 - 68 - 57 - 84 - 51 - 15 - 48 - 37 - 82 - 71 - 17 - 28 which takes only 16 moves (geometric length 49Ö2).
57(Ab) Solution by George Jelliss. 11 - 33 - 15 - 26 - 17 - 28 - 37 - 48 - 57 - 68 - 86 - 75 - 84 - 73 - 82 - 71 62 - 51 - 42 - 31 - 13 - 46 - 64 - 53 - 44 - 88. Length 35Ö2 (25 moves).
57(Ac) Solution by Siep Korteling. 11 - 44 - 17 - 28 - 82 - 71 - 53 - 31 - 13 - 68 - 86 - 75 - 84 - 51 - 15 - 48 - 66 - 88 Moves 17, Length 43Ö2 (product = 731Ö2) as compared with 784Ö2 in (a) or 875Ö2 in (b).
57(Ad) Solution by H. E. Dudeney. 11 - 55 - 82 - 71 - 17 - 28 - 46 - 13 - 31 - 86 - 68 - 57 - 48 - 15 - 51 - 84 - 66 - 88. This solution to a bishop tour of the black cells of the 8 by 8 board in 17 moves (geometric length 45Ö2) was given by H. E. Dudeney in The Tribune (Dec.3 1906), and in his Amusements in Mathematics (1917 problem 325), and is reported in W.W.Rouse Ball, Mathematical Recreations and Essays, (1956 edition page 187). However the above results show this route is not minimal in the number of moves (as seems to be implied by the context of Ball's work) nor is it the geometrically shortest length. In his 1917 text Dudeney specifies that "You can visit any squares more than once, but you are not allowed to move twice between the same two adjoining squares." This shows how carefully problems must sometimes be phrased to eliminate alternative solutions. If it takes the bishop one second to pass through a cell and one second to make a right-angled turn then, apart from the initial and final cells, he spends the same amount of time in every cell.

SOLUTIONS (B)
So that each cell on the 10 by 10 board is represented by two digits we write 10 = a.
57(Ba) Solution by Siep Korteling. 11 - aa - 99 - a8 - 31 - 13 - 8a - 79 - a6 - 51 - 15 - 6a - 59 - a4 - 71 - 17 - 4a - 39 - a2 - 91 - 19 - 2a. Taking 21 moves (geometric length 81Ö2).
57(Bb) Solution by George Jelliss. 11 - 33 - 15 - 26 - 17 - 28 - 19 - 2a - 39 - 4a - 59 - 6a - 79 - 8a - a8 - 97 - a6 - 95 - a4 - 93 - a2 - 91 - 82 - 71 - 62 - 51 - 42 - 31 - 13 - 46 - 37 - 48 - 57 - 68 - 86 - 75 - 84 - 73 - 64 - 53 - 44 - aa. Length 53Ö2 (41 moves).
57(Bc) Solution by Siep Korteling. 11 - 33 - 15 - 37 - 19 - 2a - 48 - 6a - a6 - 84 - a2 - 91 - 73 - 51 - 42 - 31 - 13 - 8a - a8 - 53 - 71 - a4 - 4a - 17 - 44 - aa. Taking 25 moves, with geometric length 67Ö2. The product is 1675Ö2 as compared with 1701Ö2 for (a) and 2173Ö2 for (b).
57(Bd) Solution by George Jelliss. 11 - 44 - 17 - 4a - 68 - 13 - 31 - 53 - 71 - a4 - 77 - 55 - 19 - 2a - a2 - 91 - 64 - a8 - 8a - 79 - 6a - 15 - 51 - a6 - 88 - aa. Taking 25-moves (geometric length 73Ö2.

COMMENTS
#(1) Here are some generalisations to boards of side 2h.
#(2) On a board of side 2h the bishop lines form h components, consisting of the diagonal path and h – 1 rectangular paths, comprising 4h – 3 moves, of total geometric length (2h – 1)²Ö2.
#(3) It is possible to make a 'unicursal tour' of these lines (i.e. to draw them in a continuous pencil stroke) since there are only two odd nodes (the ends of the diagonal). If we try to minimise the number of straight moves of the pencil in this tracing each rectangular circuit takes at least 5 moves and to connect each of these to the diagonal requires h – 1 breaks in the diagonal, making h diagonal moves, giving the minimum 6(h – 1) + 1. This sequence runs: 1, 7, 13, 19, 25, 31, 37, ...
#(4) (Ca) If we have to visit all cells but not all branches we can reduce the number of moves for each circuit to 4 by making the breaks at their corners. The procedure as for (Aa) and (Ba) then leads to a solution in (5h – 4) moves (i.e. the 4h – 3 plus h – 1 switchbacks), with total geometric length still (2h – 1)²Ö2, since each of the h – 1 circuits has one Ö2 step removed.
#(5) (Cb) To minimise the geometric length. The problem as stated is soluble on boards with h = 4k or 4k + 1 (including the trivial 2 by 2 board), but to become solvable, in a uniquely defined path, on boards with h = 4k + 2 or 4k + 3 switchbacks must be allowed.
#(6) (Cc) This is solved by a method similar to (Cd) but making the deleted rectangles as large as possible.
#(7) (Cd) Looking at a diagram of the Dudeney tour (Ad) I noted that it is based on a line 11 - 88 from corner to corner and three rectangular circuits, from each of which one single-step bishop move has been deleted. These four deleted moves form a small circuit, namely 55 - 46 - 57 - 66 - 55. The same method doesn't quite work on the 10 by 10 board since there is one diagonal 11 - aa and four rectangular circuits, so that at least five deletions are needed. My 10 by 10 solution uses eight deletions forming two small circuits. We can make 4 by 4 and 6 by 6 solutions possible by allowing switchbacks.
#(8) On a 32 by 32 board a solution is possible by deleting five small squares: {(3,3), (4,4), (5,3), (4,2)}, {(11,3), (12,4), (13,3), (12,2)}, {(19,3), (20,4), (21,3), (20,2)}, {(27,3), (28,4), (29,3), (28,2)}, {(15,9), (16,10), (17,9), (16,8)}. The first four join up the rectangles and diagonal in sets of four, and the last joins up the four resulting paths. (81 moves).

Find bishop paths on the 8 by 8 board meeting the followng conditions.
58(A): Longest maximummer bishop's tour.
58(B): Longest dual-free maximummer bishop's tour.
58(C): Minimal dual-free maximummer bishop's tour.
58(D): Minimal maximummer bishop's tour.
The maximummer condition means that at each move the bishop travels the maximum possible distance without passing through a cell already visited. If there is a choice of moves of equal length the bishop takes the one that best fulfills the other specified conditions. If two choices lead to equally good solutions there is said to be a dual.

SOLUTIONS

58(A) (26 moves) .. 15 .. 05 .. .. .. 08 26 .. 17 .. 21 .. 19 .. .. 27 .. 23 .. 20 .. 02 06 .. 25 .. 18 .. 04 .. .. 24 .. 09 .. 16 .. 13 22 .. 07 .. 11 .. 14 .. .. .. .. 03 .. 12 .. .. .. .. 01 .. .. .. 10 ..

58(B) (25 moves) 04 .. .. .. 11 .. 06 .. .. .. .. 13 .. .. .. 02 .. .. .. .. 07 .. 10 .. .. 14 .. 05 .. 09 .. 20 12 .. 15 .. 03 .. 22 .. .. .. .. 01 .. 23 .. 08 16 .. 18 .. 21 .. 25 .. .. 17 .. 19 .. 26 .. 24

58(C) (15 moves): .. .. .. 05 .. .. .. .. .. .. 07 .. .. .. .. .. .. .. .. 09 .. .. .. 02 06 .. .. .. 11 .. 04 .. .. .. .. 13 .. 16 .. .. .. .. .. .. 15 .. 10 .. .. .. .. 03 .. .. .. 08 12 .. 01 .. .. .. 14 ..

58(D) (10 moves)
d3-h7-e4-a8-d5-g8-e6-h3-f1-g2-h1.

COMMENTS Other results also mentioned by Juha, for the 8 by 8 board, were:
56 move (dualfree) queen maximummer tour (d2)
29 move (dualfree) minimal queen maximummer tour (d2)
54 move (dualfree) rooks maximummer tour (c2)
21 move (dualfree) minimal rooks maximummer tour (d2)

Construct maximal Mao and Moa tours on the 5 by 5 and 6 by 6 boards:
59(A): Maximal Mao tour in 5 by 5:
59(B): Maximal Moa tour in 5 by 5:
59(C): Maximal Mao tour in 6 by 6:
59(D): Maximal Moa tour in 6 by 6:
The Mao is the knight used in Chinese Chess (Xiangqi). It moves just like an ordinary knight but in two steps, a {0,1) wazir move followed by a {1,1} fers move, and the intermediate cell must be clear. In the case of a Mao tour this means the cell passed through must not have been visited previously. The Moa, invented by the late Dr Werner Speckmann, is similar but makes the fers move first and the wazir move second.

SOLUTIONS Juha reports these results as 'computer checked'. The Moa solutions are dual-free.

59(A) Mao, 5 by 5, 16 moves. -- -- 02 11 14 03 11 13 -- -- -- 01 06 15 12 09 04 -- -- 07 00 -- 08 05 16

59(B) Moa, 5 by 5, 16 moves. -- -- 15 06 11 14 05 12 -- 16 -- -- 01 10 07 04 13 08 -- 02 -- 00 03 -- 09

59(C) Mao, 6 by 6, 25 moves. 17 -- -- 24 19 22 10 25 18 21 -- -- -- 16 09 12 23 20 02 11 -- 15 06 13 -- 08 01 04 -- -- 00 03 -- 07 14 05

59(D) Moa, 6 by 6, 25 moves. 08 13 24 -- 06 -- 25 -- 07 12 23 04 14 09 02 05 -- 11 01 18 15 10 03 22 -- -- 20 -- 16 -- 19 00 17 -- 21 --

COMMENTS (1)
Juha also reports records so far achieved on 7 by 7 and 8 by 8 boards as:
Mao 7 by 7: 34 moves
Moa 7 by 7: 32 moves
Mao 8 by 8: 40 moves
Moa 8 by 8: 42 moves
Since the solutions for boards of sides 4, 5, 6 are 9, 16, 25. Juha suggests that the maxima for sides 7 and 8 ought to be 36 and 49, continuing the sequence of square numbers.

Update (16 February 2004): Jean-Charles Meyrignac has now in fact achieved 36 Mao moves on the 7 by 7 and has improved the record for the Mao on the 8 by 8 to 50 (disproving Juha's conjecture). Here are his solutions:

5x5: 16 jumps 1 4 0 10 0 0 11 2 5 0 3 14 7 0 9 12 0 16 0 6 15 0 13 8 17

6x6: 25 jumps 1 4 0 8 15 6 0 9 2 5 0 0 3 12 0 16 7 14 0 17 10 13 24 21 11 26 19 22 0 0 18 0 0 25 20 23

7x7: 36 jumps 1 0 25 0 19 6 37 10 0 2 5 26 0 18 3 24 11 20 7 36 27 0 9 4 0 12 17 0 23 32 21 8 15 28 35 0 0 30 13 34 0 16 31 22 33 0 29 14 0

8x8: 50 jumps 1 12 39 0 3 14 41 50 24 0 2 13 40 49 0 0 11 38 25 4 15 42 51 32 26 23 0 37 18 31 48 43 0 10 5 30 0 16 33 0 22 27 8 17 36 19 44 47 9 0 21 6 29 46 0 34 0 7 28 0 20 35 0 45

COMMENTS (2) Jean-Charles Meyrignac sends the following solutions to an alternative interpretation of the problem, in which the Mao "visits" the cell it passes through as well as the cell it moves to. He wrote a program to solve this version of the problem. The piece starts at cell (1) then moves to the two cells (2) and so on. Unused cells are marked 00. Moa tours under this rule are are the same as Mao, except that they are reversed (last jump becomes first jump, etc).

5 by 5: (10 moves) 1 2 5 4 00 00 5 2 3 4 00 6 9 00 3 6 7 10 9 8 00 10 7 8 00	6 by 6: (16 moves) 6 1 2 5 4 00 7 6 5 2 3 4 00 7 12 13 16 3 00 8 9 12 13 16 8 9 10 11 14 15 00 10 11 14 15 00	7 by 7: (20 moves) 1 2 00 14 19 20 00 00 3 2 15 14 19 20 3 4 15 16 13 18 00 00 5 4 13 16 17 18 5 00 7 12 9 10 17 6 7 8 9 12 11 10 00 6 00 8 11 00 00
8 by 8: (31 moves) 00 4 3 14 15 10 11 00 4 1 2 3 14 15 10 11 5 18 17 2 13 16 9 12 18 5 6 17 16 13 12 9 19 22 23 6 7 24 25 8 22 19 28 23 24 7 8 25 21 20 29 28 27 30 31 26 00 21 20 29 30 27 26 31	9 by 9 (34 moves) 1 2 29 30 23 24 00 00 25 00 3 2 29 30 23 24 25 26 3 4 00 28 31 22 27 26 00 00 5 4 31 28 27 22 21 34 5 6 00 32 15 16 33 34 21 00 7 6 15 32 33 16 17 20 7 00 9 14 11 12 19 20 17 8 9 10 11 14 13 12 19 18 00 8 00 10 13 00 00 18 00

60(A) by John Beasley. White Knight c1, Black King e8, White and Black play alternately. White, who is to make the first move, seeks to invade the palace. Black's defence is to sow mines; specifically, at each turn he may lob a mine onto any unoccupied square outside the palace, and this square becomes permanently unavailable to the knight. [The word 'lob' was the editor's and may have been found misleading: the King is not allowed to lob the mine directly at the knight, he must mine the square before the knight moves there.]
60(B) by John Beasley. On a large chessboard of 15 by 20 squares, White has a five-leaper at h1, Black a palace occupied by a king at h20. Black and White play alternately. Black, to play, may sow a mine on any unoccupied square. White's aim is to invade the palace. A fiveleaper is a knight-like piece that makes moves of types {3,4} or {0,5}. It takes five moves to get from h1 to h20, for example h1 - h6 - l9 - i13 - e16 - h20.
60(C) by George Jelliss. A chessboard represents an Emperor's palace. The Emperor reclines in his throne room (which can be any room he chooses). Each room of the palace has access to six other rooms which are reached by rook moves of length 1, 2 or 4 steps. A 4-step can be made freely, but a 2-step must be within a 4 by 4 quarter of the board, and a 1-step must be within a 2 by 2 sixteenth of the board. A visiting Mandarin is taken to the Entrance room of the palace, which is the uniquely determined room that is farthest from the throne room (finding this is the first "move"). The sounding of a gong indicates that the Emperor has shut one of the six doors leading to the audience rooms, and that the Mandarin must make an approach move. How should the Mandarin move to ensure he enters one of the six audience rooms with access to the throne room before all the doors are shut against him?

SOLUTIONS

60(A). The key is 1.S-e2. If the king mines only the four squares a knight move from his palace the knight's responses are completely determined and the complete solution can be presented in the usual chess problem format (with S = knight, M = mine) as follows (the final moves in each line would be 4...M-any 5.Se8):

1.S-e2 1...Mc7 2.Sg3 2...Md6 3.Sh5 3...Mf6 4.Sg7 - - - 3...Mg7 4.Sf6 - - 2...Mf6 3.Sf5 3...Mg7 4.Sd6 - - - 3...Md6 4.Sg7 - - 2...Mg7 3.Se4 3...Md6 4.Sf6 - - - 3...Mf6 4.Sd6 - 1...Md6 2.Sf4 2...Mf6 3.Se6 3...Mg7 4.Sc7 - - - 3...Mc7 4.Sg7 - - 2...Mg7 3.Sd5 3...Mc7 4.Sf6 - - - 3...Mf6 4.Sc7 - - 2...Mc7 3.Sh5 3...Mf6 4.Sg7 - - - 3...Mg7 4.Sf6

- 1...Mf6 2.Sd4 2...Mg7 3.Sb5 3...Mc7 4.Sd6 - - - 3...Md6 4.Sc7 - - 2...Mc7 3.Sf5 3...Md6 4.Sg7 - - - 3...Mg7 4.Sd6 - - 2...Md6 3.Se6 3...Mg7 4.Sc7 - - - 3...Mc7 4.Sg7 - 1...Mg7 2.Sc3 2...Mc7 3.Se4 3...Md6 4.Sf6 - - - 3...Mf6 4.Sd6 - - 2...Md6 3.Sd5 3...Mf6 4.Sc7 - - - 3...Mc7 4.Sf6 - - 2...Mf6 3.Sb5 3...Mc7 4.Sd6 - - - 3...Md6 4.Sc7

The possible four-move routes of the knight e2 to e8 form a four-dimensional hypercube as illustrated below. Denoting the palace e8 as 0000 and e2 as 1111 the four cells a knight move from e8 can be named 1000, 0100, 0010, 0001 from left to right, the six cells of the hypercube two knight moves from e8 can be named 1100, 1010, 1001, 0110, 0101, 0011, where for example 1100 is the cell that can be reached from 1000 or from 0100. The four cells a knight move further on are 1110, 1101, 1011, 0111 and these are a knight move from 1111. If the king mines 1000 then the knight must move to the complementarily named cell 0111. If the king then mines 0100 the knight must move to 0011. If the king then mines 0010 the knight moves to 0001 and next move enters the palace. Each sequence of mining of the four cells a knight move from the palace leads to a uniquely defined approach route by the knight. If the king lobs his mines further afield than a single knight move then the responses of the knight are less strictly determined. For instance if the king mines 1110 then the knight can move to any of 1101, 1011, 0111. If the king mines 1010 then the knight moves to those cells that do not lead to 1010, namely 1101 or 0111.

60(B). Here the five-move fiveleaper routes from h1 to h20 form a five-dimensional hypercube, and the problem works on similar principles to 60(A). As in 60(A) the fiveleaper could start on c1 with White to move c1 - h1 to reach the given start position. In the diagram of the five-leaper moves it should be noted that the antelope moves, those of {3,4} type, form two four-dimensional hypercubes and the vertical {0,5} moves represent a translation by which one of these hypercubes is transformed into the other. Some of the {0,5} moves in the diagram overlap.

60(C). Here is an example solution: 1. Emperor chooses f5 as throne room, 1... Mandarin enters c4 (the entrance is always the diametrally opposite cell), 2. Emperor closes f1, 2... Mandarin c8 (diametrally opposite again), 3. Eb5, Mg8, 4. Ef6, Mg7, 5. Ef7, Mg5, 6.Ee5, Mh5. This problem was of course inspired by John's problem 60(A), which he presented at the BCVS AGM held at his home in 2003. The moves connecting the rooms of the palace are those of a hyperwazir as defined by me in Chessics 1982 (issue 13 page 13) in the article headed "Chessics and the I Ching". They make the whole 64-cell board into a six-dimensional hypercube, presented in the most compact way possible.

Instead of the representation of the cells by binary digits, an alternative approach is to label the six audience rooms, one step from the throne room, A, B, C, D, E, F, then to label the rooms two steps from the throne room by the names of the two audience rooms to which they give access (i.e. AB links to A and B and so on). Rooms three steps away have three labels and so on. This procedure gives the pattern:

4-ABDF	3-ABF	5-ABDEF	4-ABEF	3-ABD	2-AB	4-ABDE	3-ABE
3-BDF	2-BF	4-BDEF	3-BEF	2-BD	1-B	3-BDE	2-BE
3-ADF	2-AF	4-ADEF	3-AEF	2-AD	1-A	3-ADE	2-AE
2-DF	1-F	3-DEF	2-EF	1-D	0	2-DE	1-E
5-ABCDF	4-ABCF	6-ABCDEF	5-ABCEF	4-ABCD	3-ABC	5-ABCDE	4-ABCE
4-BCDF	3-BCF	5-BCDEF	4-BCEF	3-BCD	2-BC	4-BCDE	3-BCE
4-ACDF	3-ACF	5-ACDEF	4-ACEF	3-ACD	2-AC	4ACDE	3-ACE
3-CDF	2-CF	4-CDEF	3-CEF	2-CD	1-C	3-CDE	2-CE

The Mandarin starts at 6. If the Emperor closes B, the Mandarin goes to cell 5 that does not contain B, that is ACDEF. If then the Emperor closes F, the Mandarin goes to cell 4 that does not contain B and F, that is ACDE. And so on.

61(A): By cuts parallel to the edges, no pieces being turned over, transform two squares of sides 3 and 4 into one square of side 5 using 4 pieces, one of which is a unit square. There are two distinct solutions.
61(B): By cuts parallel to the edges, no pieces being rotated or turned over, make the transformation of rectangle 64×81 to square 72×72 using 3 pieces formed with only 7 cuts.
61(C): In the dissection of two smaller squares of dfferent sizes to form a larger square, find positions of the overlaying lattice of larger squares that (a) dissect both smaller squares symmetrically, (b) dissect both smaller squares similarly (in the geometrical sense).
61(D): Given squares of sides 1 and Ö3 units, with sides parallel, dissect the two squares into five pieces that can be combined, without rotation or turning over, to form a square of side 2. (a) with two pieces the same (i.e. congruent), (b) with all pieces different. [Chris wrote to me after I had published this problem to point out that in 61(Da) "the 'Centre Dudeney' solution that you give might be taken as solving this problem, since 4 identical pieces implies 2 identical ones!" and for 61(Db): "surely a solution from any of the continua (including any non-central Dudeney and any variation of Block-Slide D) would do?". The Block-Slide D referred to is the diagrammed solution below, and 'variation' is used in a technical sense defined in his thesis. More details to appear in a subsequent issue. Luke Pebody pointed out that the Perigal solution also solves this case. I think I intended to imply that the solutions should be specific to the dimensions cited, but perhaps I should have added further conditions.]
61(E): Given squares of sides 4 and 2 + 3Ö2 dissect them into five pieces that can be combined to form a square of side 6 + Ö2, including two equal triangles. [Here I also meant a solution specific to the dimensions.]

SOLUTIONS

61(A). Solution as diagrammed. In each case one piece is rotated. Gabriele Carelli finds another solution under the stated conditions: in (a) remove the unit square from a corner of the 3 by 3 square and divide the 4 by 4 square into the P-shape and the remaining squares.

61(B). Solution as diagrammed. No piece is rotated. This type of "double step" dissection becomes possible when q + 1 is a composite number. Recall that the small cells here are not squares but 8 by 9 rectangles.

61(C). Each solution takes 6 pieces. The symmetric solution passes through the centres of the smaller squares. The similarity solution is achieved by placing the corners of the large squares at points on the small squares that divide the edge in the ratio ab/(a+b). Gabriele Carelli notes that it is possible to prove that, with this position for the corners of the big square, we never cut off a corner of the middle-sized square, no matter what the relative sizes of the two smaller squares.

61(D). In the simplest dissection for this case (a) the unit square is untouched, another unit square is cut from a corner of the Ö3 square, and the remaining gnomon is converted into a 1×2 rectangle. In (b) a strip is cut from one side of the extra unit square and the rest is left attached to the small triangle.

61(E).

Divide each face of a regular tetrahedron into three congruent segments by perpendicular bisectors of the sides. Then use one of three different colours to colour each segment under the rule that segments that meet along a line or edge cannot be the same colour. How many distinguishable tetrahedra can be made?

SOLUTION
There are two fundamental solutions which expand by interchange of colours into five distinguishable tetrahedra. Assume the colours are blue, green and red. In Diagram I the three colours run clockwise in alphabetical order round each face and it is easily seen that this is the only possible assembly of four faces under the clockwise constraint. If red and green are interchanged then the colours run anti-clockwise on every face creating a distinguishable solid and again there is only the one way to put the faces together. In Diagram II the colours are to run alphabetically clockwise on two faces and anti-clockwise on the other two. When one pair has been coloured the positions on the other two are forced. The colours can then be cycled from BGR to GRB and then RBG on the clockwise faces to give two more solutions. Again the colourings on the other two faces are forced but cycle anti-clockwise similarly. The three solids so produced can be distinguished by noticing the changing pairs of colours along the edge where the two clockwise faces meet. Since a three/one division of the face rotation is not possible the two arrangements from Diagram I and three from Diagram II give the total of five distinguishable solids.

Nick has asked me to restate this problem. The original statement, in full, was as follows:

A question of volume The cube is 3×3×3. All corners are 90 degrees. It is a perfect cube. A hole is bored through the centre of the side face along the X axis. This is repeated with a hole through the top face, along the Y axis. This is again repeated, through the front face, along the Z axis. All holes have a diameter of exactly 1. All holes are on the centre lines. All axes intersect at right angles. How do you calculate the volume of the material removed from the holes? The actual result is irrelevant. Only the method is required.

The above is the exact figure shown in his original statement of the problem.

SOLUTION (by George Jelliss)

This is my solution which I am now reasonably sure gives the correct numerical result.

By looking up a few formulas I came to the conclusion that the volume of material removed is 9p/4 – Ö2 = 5.6543699 (in cubic inches). As a rough check: (a) the volume of the cube is 3^3 = 27 cubic inches and if the holes bored are of square cross-section the volume removed would be 7 cubic inches. (b) On the other hand if we approximate the central volume as six cones meeting at the centre point attached to six short cylinders (like six pencils pushed into the holes), the volume works out as 7p/4 = 5.4977871. So these two estimates provide upper and lower bounds for the volume.

Here is the detailed working: (a) The formula for the volume of a cylinder of height h and radius r is h×pr^2, so for h = 1, r = 1/2 we get: U = p/4. (b) The formula (known to Archimedes) for the volume common to two mutually orthogonal cylinders of height h and diameter d is (2/3)d^3, so for d = 1 we get V = 2/3. (c) The formula for the volume common to three such cylinders is (2 – Ö2)d^3, so for d = 1 we have W = 2 – Ö2. I found formulas (b) and (c) in The Penguin Dictionary of Curious and Interesting Geometry by David Wells (1991 pp.118-119), where he quotes the source: M. Moore, 'Symmetrical intersections of right circular cylinders', Mathematical Gazette, No.405 (1974).

So the volume of the hole in the central 1×1×1 cube consists of (1) the volume common to all three cylinders, W. (2) the volume common to pairs of cylinders but not to all three, that is (V – W) three times. (3) The volume due to each single cylinder, that is (U – 2V + W) three times, where W has to be added back in. (It may be helpful to visualise this calculation by means of a Venn diagram of three mutually intersecting circles: U being the area of each circle, V being the area of each lentil formed by the intersection of two circles, and W being the central area.) This gives: W + 3(V – W) + 3(U – 2V + W) = 3U – 3V + W. Finally to this we have to add 6U for the six tunnels leading into the central cube.

I've not seen the original paper in Mathematical Gazette, but Paul Cleary directs us to an account at mathworld, where the required formulas are derived by methods using integration. I am grateful to Gabriele Carelli and Paul Cleary for helpful correspondence on this problem. However, in view of the original wording of the question, I still wonder if there is not a simpler method of solution, perhaps purely geometrical or trigonometric, not involving calculus.

64(A) and (B) by Jean-Charles Meyrignac: Find longest non-intersecting knight paths on (A) the English 33-cell and (B) the French 37-cell Solitaire Boards.
64(C), (D) and (E) by George Jelliss: Construct 31-move open tours on the 33-cell solitaire board with the following properties: (C) the two end cells and the omitted cell are all adjacent, and all moves are within the border, (D) the centre cell is omitted and the tour goes outside the border once, (E) the centre cell is omitted and, when the cells visited by the knight are numbered in sequence, the numbers in the diametrally opposite pairs of cells differ by the constant value 4.
64(F) by George Jelliss: The Snake Pit: On the 82-cell board shown, pass from one side to the other, joining the two marked cells by a non-intersecting knight path of maximum length.

SOLUTIONS

64(A), (B) (A) 19 moves, (B) 20 moves (symmetric path). These figures were kindly provided by J-C.M.

64(C), (D), (E)
On the 33-cell solitaire board there are 17 white cells and 16 black (assuming the corners are coloured white). A closed tour is not possible because of the odd number of cells. An open tour if possible must start and end on the majority colour white cells, but moves through the black cells a4, d1, d7, g4 form an 8-move short circuit (dotted moves in first diagram), so no open tour is possible.

A tour omitting one cell must omit a white cell and must include 7 moves of the 8-move circuit. Because of the octonary symmetry of the circuit we can take a4-c5 as the first move without loss of generality. Under the restriction that moves must be within the area of the cross, the end cell must be on one of b4, c1, c7, e1, e7, f4, and the unused cell at one of a3, a5, d2, d6, g3, g5, since otherwise one or both of the 12-move short circuits shown (in the first diagram) are forced. A shaped board solution with start, finish and omitted cells adjacent is shown in the second diagram, solving 64(C). If the unused cell or the end cell is at the centre then the tour must go outside the border at least once, as in the third diagram, solving 64(D). The tour in the last diagram is piece-wise symmetric, so when numbered the diametrally opposite cells differ by the constant value 4, solving 64(E). [These notes were inspired by a puzzle proposed by Angus Lavery in Games & Puzzles No.2, May 1994, page 34.]

64(F). The reason for calling this 'The Snake Pit' is evident from the solution diagram.

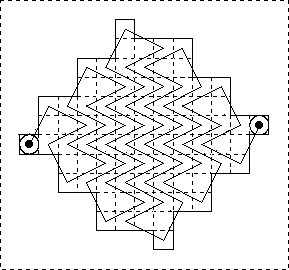
The 20 omitted cells happen to occur in a regular pattern of 10 'domino' pairs.

John Beasley notes that in addition to the examples previously cited it is possible to do:
10 in 10 lines of 3 on 5 by 6 board: (0,0), (1,2), (2,0), (2,1), (2,4), (3,0), (3,2), (3,3), (4, 4), (5, 4).
9 in 9 of 3 with no two lines parallel on 8 by 8: (a) a4, b4, c6, d3, d7, d8, f4, g2, h1. (b) a8, c7, d7, e4, f3, g1, g5, g6, h7.
He gave these results and some others in his British Endgame Study News, Special Number 13, December 1998.

Our problems for solving were:
65(A) Plant 11 trees in 6 lines of 4 on a grid as small as possible.
65(B) Plant 21 trees in 12 lines of 5 on a grid as small as possible.
65(C) Plant 13 trees in 9 lines of 4 on a grid as small as possible.

SOLUTIONS

65(A) 11 in 6 lines of 4. The pattern can be regarded as a distortion of a 3 by 3 array with the three parallel rows and three parallel columns each made to converge to a point. My two (symmetric) solutions on a board 61 by 61 were:
(a) (0,0), (0,20), (0,30), (0,60), (12,24), (15,15), (20,20), (20,0), (24,12), (30,0), (60,0).
(b) (0.30), (20,20), (20,40), (30,30), (36,12), (36,48), (40,20), (40,40), (45,30), (0,60), (60,60).
Jean-Charles Meyrignac solves this case using a board only 11 by 19 in two ways:
(a) (0,0), (0,6), (0,9), (0,10), (2,8), (6,4), (6,6), (10,0), (12,2), (15,0), (18,0)
(b) (0,0), (6,6), (9,9), (10,0), (10,40, (10,8), (10,10), (12,6), (14,2), (15,0), (18,0).

65(B) 21 trees in 12 lines of 5 on a board 61 by 61. (0,0), (0,±15), (0,±30), (±15,0), (±30,0), (±10,±10), (±30,±30), (±8,±18). This is one of two solutions of this case given by H. E. Dudeney in Amusements in Mathematics 1917 problem 209 (though not fitted to a board). Note that the four points (±18, ±8), which are also intersection points of the lines, do not count as points of the plantation, since no trees are planted there. The pattern is simply that of the four corners of a square joined to the four mid-sides of the squares (giving 24 in 8 lines of 6) with four intersections removed and the centre point inserted.

65(C) 13 trees in 9 lines of 4 on a board 169 by 253: (0,0), (42,84), (56,112), (70,70), (84,28), (84,63), (84,84), (84,168), (96,72), (105,105), (112,84), (126,42) (252,84). In this arrangement there are no unused intersections. The board is too large to show all the small cells. It will be noted that all the coordinates are multiples of 7 except (96, 72) so most of the array can be drawn on an array of points 24 by 36 units, each unit representing 7 smaller units, as was done in drawing this figure.

COMMENT

A question I have never quite resolved is: Can all such plantations be fitted on a grid? In other words can all the coordinates of the points always be made integral numbers, or is there an 'uncoordinable' configuration? There are many other cases to consider and we will no doubt return to this problem when further results are available.