Back to Non-Intersecting Page.
This page has been created (16 April 2015) to separate the results for longer leapers and other pieces from those for the knight.
Further results can be found on the Alex Black website.
It has of course long been known that a rook can tour any rectangular board without crossing its own path (Rudrata c.900 gave a 4×8 tour).
This makes the tour in effect a wazir, {0, 1}-leaper, tour.
T. R. Dawson Fairy Chess Review August 1944 (problem 6038) gave an 8×8 open tour of 52 moves for the gnu (knight + camel) that is {1, 2} + {1, 3}-leaper.

The problem for the higher free leapers, giraffe {1, 4}, zebra {2, 3} and antelope {3, 4} on the 8×8 board was solved by George Jelliss in Chessics (vol.1, issue 9) 1980.
Robin Merson, in a letter dated 16 June 1991, accompanied by computer printed diagrams, confirmed these results and extended them to larger boards.
One open and one closed path for each of camel, zebra, giraffe and antelope, on boards of side 8, 9 and 10 are shown in the following diagrams.
The camel, {1, 3}-leaper, is of course confined to cells of one colour if the board is chequered.
8×8 board.
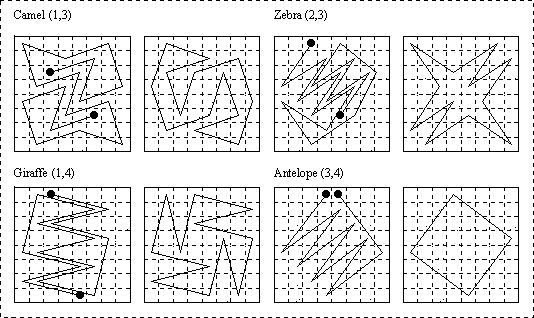
9×9 board (On this the giraffe can do no better in a closed tour than it does on the 8×8).

10×10 board.

Robin also gave solutions for antelope on 11×11, on which the unique closed path takes the form of a tetraskelion similar to those for the 7×7 knight (1, 2) and 9×9 zebra (2, 3); an evident progression. These cases were diagrammed in a brief report on his work in Variant Chess, (vol.1, nr.6, 1991).
The following is a table of Robin Merson's results on these longer leapers. The figures in brackets give the number of different tours found; thus (1) indicates a unique solution.
| 8×8 | 9×9 | 10×10 | 11×11 | |||||
| open | closed | open | closed | open | closed | open | closed | |
| camel | 17 (1) | 14 (5) | 23 (14) | 20 (20+) | 29 (1) | 26 (1) | ||
| zebra | 17 (3) | 12 (12) | 25 (1) | 24 (1) | 32 (9) | 28 (7) | ||
| giraffe | 15 (2) | 12 (1) | 19 (1) | 12 (1) | 25 (11) | 20 (2) | ||
| antelope | 9 (5) | 4 (2) | 13 (4) | 8 (3) | 17 (15) | 12 (7) | 25 (4) | 24 (1) |
The results in the above table have not been updated. See the Alex Black site for more details.