
This is a continuation of the Note devoted to Open Knight's Tours of Three-Rank Boards, and uses some results proved therein. In particular, the result of Theorem 3.1 implies that the end-files of closed tours show either the comet (A) or 3×4 tour (B). Closed tours can thus be classified by their end-formations as of types AA, BB or AB. Those of type AB are all asymmetric. Similarly the result of Theorem 3.2 provides a method of extending any closed tour by four files.
Closed knight's tours exist on all boards 3×2k except 3×4, 3×6 and 3×8.
Proof: (a) No closed tour is possible on the 3×4 board, since the passages through a1, a3 and d2 are fixed and form a six-move short circuit. (b) No closed tour is possible on the 3×6 board since the passages through the cells a2 and e2 form a four-move short circuit. (c) No closed tour is possible on the 3×8 board since the passages through the six end cells are fixed and we may also fix b1-c3 and b3-d2 without loss of generality (since the alternative choice b3-c1 and c1-d2 is merely a reflection of this case), and we now have two choices; if g1-f3 and g3-e2 then e2-c1 and d2-f1 are forced; if g3-f1 and g1-e2 then e2-c1 and d2-g3 are forced; these forced moves complete 18-move short circuits. (d) Example tours 3×10 and 3×12 are shown hereafter. (e) Tours on all larger boards 3×2k can be constructed from the 3×10 and 3×12 examples by repeated application of the four-file extension method explained in Part 1.

In his 1759 paper Euler expressed the view that closed tours were not possible on any boards with side less than 5 and his authority was so great that his statement was not questioned for over 150 years. The existence of closed tours on 3-rank boards was first shown by Bergholt in 1917.
Symmetric closed tours exist on all boards 3×2k except 3×4, 3×6, 3×8 and 3×12.
Proof: (a) On 3×4, 3×6 and 3×8 no closed tours exist as proved above. (b) On the 3×12 board a closed tour with reflective symmetry is not possible since such a tour requires an odd × singly-even or an even × even board. If a tour with rotational symmetry exists it must pass twice through the centre, i.e. contain the moves f1-g3 and f3-g1. The moves through a1, a2, a3, b2 and l1, l2, l3, k2 are fixed, and we can take b1-c3, j1-k3, b3-d2, i2-k1. We must then have either (1) d2-f1, g3-i2 in which case c1-e2-g1 and f3-h2-j3 are forced, or (2) d2-f3, g1-i2 in which case c1-e2-g3 and f1-h2-j3 are forced. In each case a 24-move short circuit is completed. (c) Any symmetric tours of sizes 3×10, 3×14, 3×16 and 3×20 (see hereafter) can be extended by four files at each end by the method explained in Part 1 to provide symmetric tours on all larger boards.

There are 26 formations that can occur on the two centre files in rotationally symmetric closed tours 3×n, consisting of 18 on boards 3×(4k+2) and another 8 on boards 3×4k.
Proof: (a) If the symmetry is eulerian the moves through the upper and lower cells of the two middle files can be taken in five ways: LL, VV, AL, LV, AV (not AA as it forms two circuits). If the symmetry is bergholtian the moves through these cells can be taken in four different ways: NN, NS, NZ, SZ (not SS, ZZ which form closed circuits). In either type of symmetry there are four ways in which the centre cells can be taken: I, U, C and D.
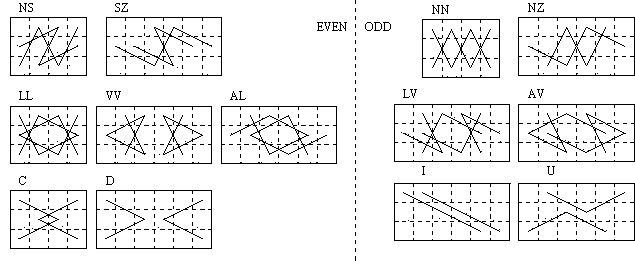
(b) Each formation on the two central files can thus be represented by a three-letter code, e.g. ALU or NNC. The codes that include one or more of the reflectively symmetric components LL, VV, NN, C or D each represent one pattern, but in the other cases there are two ways of combining the formations. Those in which the centre-cell formation is reflected can be distinguished by an asterisk, e.g. NZI and NZI*. This gives 48 formations.
(c) The 14 formations LLC, LLD, VVC, VVD, ALC, ALD, AVI, AVI*, AVU, AVU*, LVI, LVI*, LVU, LVU* cannot occur in any symmetric tour since joining the loose ends in the same way on each side results in two circuits instead of a single tour (LLC and VVC in fact already form two circuits). This reduces us to 34 formations.
(d) The case NNC forms a single circuit but not using all the cells of the 3 by 4 rectangle it occupies. In the case SZD a six-move short circuit is forced so no tour is possible. In the cases NSD, NZC, VVI, VVU, LVC, AVC iterative construction shows that these central formations lead to end-formations which, when extended further, lead only to the same end-formations (diagrams of these, being rather extensive, have been omitted). This means that these paths can be extended to any length, but the ends of the tour can never be squared-off to complete a rectangle, so no tours derive from these cases. This reduces us to the 26 formations stated in the theorem.
(e) A necessary condition for a tour to be possible is that the number of cells needed to join up the loose ends on one side of the central formation, plus the number of cells used in that half of the formation, must be of the same parity (even or odd) as that of half the board, i.e. odd on 3×(4k+2) and even on 3×4k. (The partial components are classified as odd or even according to this criterion in the figure above). The 18 cases possible in tours on 4k+2 boards are: NSI, NSU (occurring on 3×10), SZI, SZI*, ALU, ALU*, LVD, AVD (on 3×14) and NND, NZD, NSI*, NSU*, SZU, SZU*, LLI, LLU, ALI, ALI* (3×18). The 8 cases possible in tours on 3×4k boards are: NZI, NZI*, NZU, NZU*, SZC (possible on the 3×16 board) and NNI, NNU, NSC (which occur in 3×20 tours).
The numbers of tours in reflective and rotational symmetry on boards 3×(4k+2) are equal.
Proof: Consider the possible formations on the two central files. These formations are found to occur in reflective and rotational related pairs. The reflective forms, illustrated below, are denoted by the same letters as for the rotational forms but underlined (NN, LL, VV, C, D, are in fact the same as the rotational cases).

This is illustrated for the case of the 3 by 14 board in the catalogue below.
The same arguments as in the previous theorems show whether tours are possible; in fact each reflective tour can be formed by reflecting half of the corresponding rotational tour. This equality was conjectured by me in Chessics (#22 1985 p.65) but a more complete proof is given above. It will be found that in the eight cases that apply on 4k boards the transformation from rotational to reflective alters a tour to a pseudotour (a superposition of circuits). This result is thus compatible with the fact that tours with reflective symmetry are not possible on 3×4k boards.
This and the 5×6 board are the smallest rectangles on which closed knight's tours are possible. Ernest Bergholt (1917) was the first to discover a 3×10 closed tour, and he and G.L.Moore (1920) found all six solutions, although Kraitchik (1927) was the first to publish all six. Two are centrosymmetric tours (of the bergholtian type in which two moves cross at the centre, as opposed to the eulerian type which circles the centre), two axisymmetric (of the sulian type in which the axis does not pass through any cell-centre) and two asymmetric.
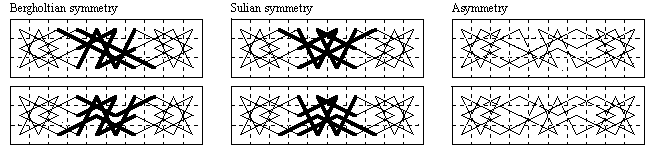
The patterns formed by the moves through the cells of the two central files in the symmetric tours are emphasised, since they are used to classify tours on longer boards. Those on the 3×10 board are denoted NSI and NSU.
A closed tour was first found by Bergholt (1917). There are 44 closed tours, none symmetric (for proof see Theorem 3.6). Each diagram shown generates 4 tours by twiddling the end components. Twelve of these tours are compartmental (3×4 + 3×8).
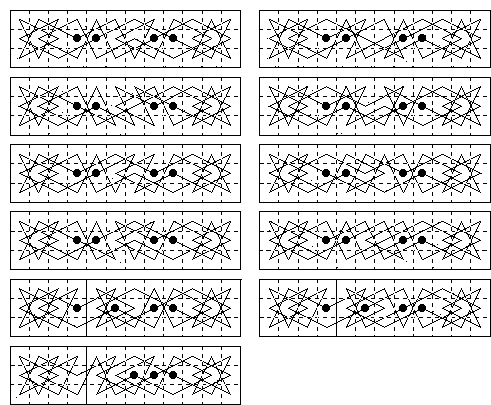
There are 396 closed tours of which 24 are symmetric. The tours can be classified as 318 of type AA (20 symmetric), 6 of type BB (4 symmetric) and 72 of type AB, where A denotes the comet end formation and B the 3×4 end formation. Here are diagrams of the 24 symmetric tours, 12 rotational on the left and 12 reflective on the right. (Of the rotational ones the first 8 are eulerian and the other 4 are bergholtian). Another 20 asymmetric tours can be formed by twiddling the components of these tours.

In a tour of AA type, each A uses 10 cells. The remaining 22 cells are covered by two paths, linking the As together, and the tours can be classified according to the way these 22 cells are divided between the two paths. In the symmetric AA tours and the asymmetric tours derived from them the 22 cells are shared out equally 11:11, and there are another 8 of this type. The 318 AA tours are distributed: 11:11 (46), 10:12 (12), 9:13 (28), 8:14 (24), 7:15 (40), 6:16 (20), 5:17 (32), 4:18 (80), 3:19 (4) and 2:20 (32).
The following eight diagrams generate the 72 AB tours (one diagram generates 16, the others 8).

There are 24 symmetric closed tours, all bergholtian. 20 have ends AA and 4 BB. The centre patterns are NZI, NZI', NZU, NZU', SZC. The first six diagrams generate 2 and the others 4.

There are 292 symmetric closed tours. These consist of 146 rotational and 146 reflective. The partial diagrams below are of ten rotational examples showing the centre formations not possible on smaller boards. There are 6 bergholtian and four eulerian:

There are 176 symmetric closed tours, all Bergholtian. The following three centres are those not possible on boards shorter than length 20.

Table of numbers of closed knight tours on 3-rank boards
n 10 12 14 16 18 20 S 4 0 24 24 292 176 G 6 44 396 3868 37078 362192
G = number of geometrically distinct tours, S = number of geometrically distinct symmetric tours. For those who, for some reason known only to themselves, wish to calculate the number of tour diagrams the formula is: T = 4G – 2S.