Here we consider tours by the 'big beasts', Camel, Zebra, Giraffe, Antelope, etc combined together to form even bigger beasts, or augmented with knight, bishop or rook move. Other examples of pieces with two modes of movement will be found in the sections on King, Queen, Emperor, Empress, and other Augmented Knights. The Fiveleaper has its own page. Pieces with three or more move types, including long skew leaps, will now be found on the Multimover pages.
2×4. Two biaxial closed tours by Wazir + Camel

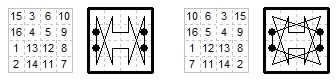
4×4. Biaxial magic tours (nondiagonal) with biaxial symmetry, when the two end-points of the path are joined up to give a closed path. (Jelliss Chessics #26 1985).
4×6. Biaxial magic rectangles (Jelliss 10 Aug 1991). The first of these is also given by Trenkler (1999). Magic sums 50 and 75.
4×8. Biaxial magic rectangles (Jelliss 17 Oct 2014). Magic sums 66 and 132.
6×6. The smallest possible square tour by this amphibian is 6×6. This symmetric example has the minimum of two (0,3) moves (Jelliss undated).
This is our first combination of two skew movers.
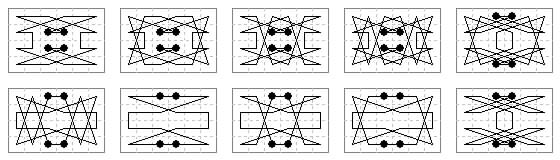
4×4. The 4×4 open tour with one camel move is by S. H. Hall (Fairy Chess Review Aug 1944). The second is by E. Huber-Stockar (FCR Jun 1944 ¶6017) and has rotary symmetry (not quite birotary), and it was noted (Huber Stockar FCR November 1939 problem 3937) that four can be joined to form an 8×8 quaternary tour. The third (Jelliss 12 August 2022) also has rotary synmmetry, but with camel moves crossing at the centre.
5×5. Symmetric open tour by E. Huber-Stockar (FCR 1941 ¶4710) with moves in only half of the possible directions. Also a similar tour (Jelliss August 2022), four copies of which can be combined by knight links to form a closed quaternary 10×10 tour.
6×8. Rotary tours of alternating knight and camel moves. The first by E. Huber-Stockar (FCR 1942 ¶5085) is in Eulerian symmetry with opposite cells differing by 24. The second (Jelliss 12 August 2022) is in Bergholtian symmetry with opposite cells adding to 23 or 71, and with camel moves crossing at the centre point.

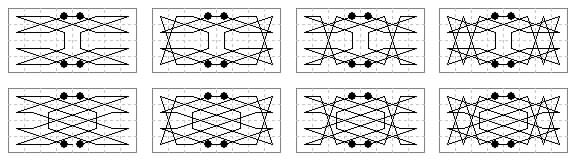
8×8. A symmetric gnu tour of alternating knight and camel moves joining two half-board tours was given by S. H. Hall (Fairy Chess Review Aug 1939). F. Hansson (FCR Nov 1939 ¶3936) gave a gnu tour with axial symmetry and minimum two camel moves. This is just two half-board tours by knight joined by camel moves.
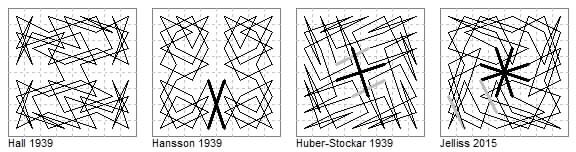
E. Huber-Stockar (same issue ¶3937) gave an 8×8 gnu tour in approximate quaternary symmetry in which two camel moves cross at the centre (shown bold in our diagram). The four halves of these moves form part of the quaternary symmetry. The only deviation from quaternary are the two 1-1 knight moves shown in grey which have no corresponding pair. Drawing this tour inspired me to try an alternating tour with four camel moves crossing (Jelliss Feb 2015), this is asymmetric, departing from symmetry with the two grey moves at the bottom left.
6×6. E. Huber-Stockar (FCR ¶5395 Dec 1942 and Feb 1943) gave a 6×6 symmetric tour by this piece. For clarity the rook moves are only indicated partially in our diagram. This works since there is only one such move in each rank and file.
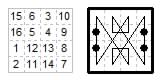
4×4. Magic tour (nondiagonal) with biaxial symmetry when the two end-points of the path are joined up to give a closed path. The black dots mark 1, 8, 9, 16. (Jelliss Chessics #26 1986).
4×6. Biaxial (Jelliss 10 Aug 1991).
4×8. Biaxially symmetric magic tours. Results from a partial enumeration 18 Oct 2014.

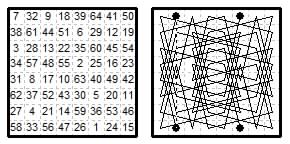
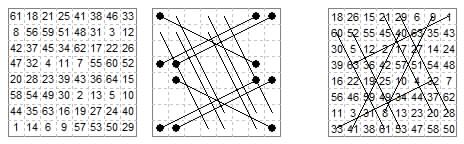
PUZZLE: Here is a cryptotour on the 6×6 board. It requires a reentrant tour by a 'bison' which moves in {1,3} and {2,3} leaps. The tour is comprised of camel {1,3} moves with only one zebra {2,3} move. The solution (see end of page) is a verse I wrote on seeing the first Bison chess problem.
some by if bison may 've
or chance you camel ing in
and camel chess 'swith eye or
son son 'sgo white seen you
stripe bison to jumps 'swith mak
lar black humps son zebra set
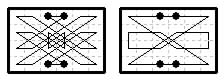
8×8. A closed tour by this piece was given by O. E. Vinje (FCR Nov 1939 and Feb 1940). It can be regarded as Zebra + double-length Zebra. In the diagrams the two types of move are shown separately since they overlap in places due to switchbacks.
2×8. On the 2×8 board there are 8 magic tours by {0,1}+{1,4}, permuting magic king tours.

4×8. Biaxially symmetric magic tours. Results from a partial enumeration 17 Oct 2014.

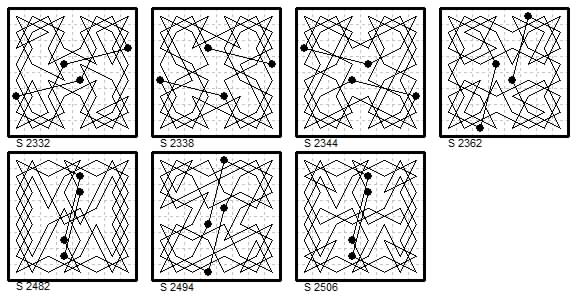
8×8. Magic two-knight rotary tours Le Siècle
(1) ¶2332 (18 Apr 1884) 224/232 by Reuss.
(2)¶2338 (25 Apr 1884), diags 260±12 by Béligne.
(3) ¶2344 (2 May 1884) 260±20 by M. A. F.
(4)¶2362 (23 May 1884) 312/272 by M. A. D. a Rouvres.
(5) ¶2482 (10 Oct 1884) 260±4 by Béligne.
(6)¶2494 (24 Oct 1884) 264/224 by Palamede (Ligondes).
(7) ¶2506 (7 Nov 1884) 260±32 Anon.
8×8. Magic Two-Giraffe Tour (Jelliss 2013): two copies of a 32-cell giraffe tour joined 32-33.
The {2,4} Lancer leap is a knight move extended to twice the length and passing over a cell centre. Lancelot is a proposed name for this little studied piece, combining Wazir and Lancer.
4×8 Two biaxially symmetric 4×8 magic tours from a partial enumeration. When numbered from the quarter points these remain magic in the files but take two different sums in the ranks.

Extending the knight move in a straight line leads to the Nightrider, analogous to the Rook along lateral lines or the Bishop along diagonals. Little work seems to have been done on Nightrider tours. Using its {2,4} move the nightrider can make open tours of the 3×5 board.
A knight tour with ends a {2,4} leap apart has both end cells the same shade so requires an odd board. In the notes on oblong boards PDF #4 we show the ten tours of this type on the 3×9 board.
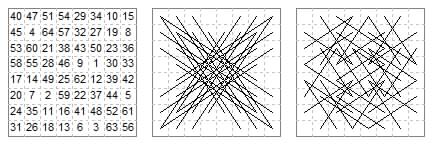
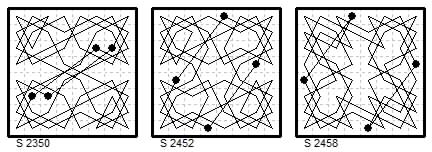
8×8. Magic two-knight tours Le Siècle
(1) ¶2350 (9 May 1884) rotary, diagonals 260±4 by Palamede (Ligondes).
(2) ¶2452 (5 Sep 1884) rotary, diagonals 296 & 288 by Béligne.
(3) ¶2458 (12 Sep 1884) rotary, diagonals 248 & 292 by Palamede (Ligondes).
2×8. On this board there is one magic tour by {0,1}+{1,5}.
4×6. Biaxial (Jelliss 10 Aug 1991).

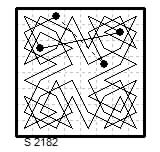
8×8. Magic two-knight tour from Le Siecle ¶2182 (26 Oct 1883) by Palaméde (Ligondès) with {3,3} closure move. The symmetry of this is described as 'pivotante quadrangulaire' diagonals 368 & 144.
4×6. Biaxial magic (Jelliss 10 Aug 1991).
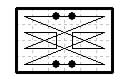
This was the last of 29 tours by two-pattern movers found on this board.
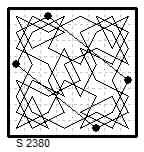
8×8. Magic two-knight tour Le Siècle (1) ¶2380 (13 Jun 1884) rotary, diagonals 280 & 296 by M.A.F. (Feisthamel).
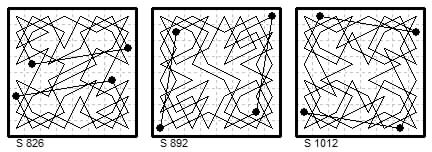
8×8. Magic two-knight tours Le Siècle
(1) ¶826 (27 Jun 1879) rotary, diagonals 260±4.
(2) ¶892 (12 Sep 1879) rotary, diagonals 296 & 188.
(3) ¶1012 (30 Jan 1880) rotary, diagonals 260±20.
All 4×8 knight tours are open, since the end cells have to be in the top and bottom edges. A nightrider however can make a closed tour. Two of the edge-hugging tours can be regarded as nightrider tours, since their end points are a {3,6} move apart. Here are two, not quite of the edge hugging type. One from a Turkish ms (c.1850) and one in which the central link is also in the nightrider line (Jelliss 2014).
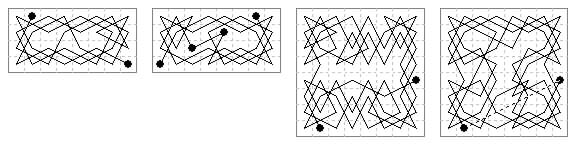
The first 8×8 tour is also from the Turmish ms, the other (Jelliss Sep 2014) is of squares and diamonds type, and both have the {3,6} closure move.
A symmetric 8×8 tour using {2,4}{3,6} moves was sent to me by T. W. Marlow on 4 Apr 2001. It uses only moves in the knight direction, though no actual single knight moves. In the diagram I show only the twelve {3,6} moves (including the closure move 64-1). The dots indicate points where switchbacks occur, for instance 13-14-15-16 are all in the same nightrider line.
The second example above is by Juha Saukkola. 'Nightrider Tours without Knight Moves' The Games and Puzzles Journal #20 (online) May-Aug 2001. The tour is symmetric, the first half 1-32 using the cells of the even ranks, the second half the odd ranks. The eight triple knight moves {3,6} are drawn in, the others are all double knight moves {2,4}.
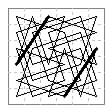
12×12. Kraitchik (1927) gave a closed root-50-leaper tour of the cells of one colour on a 12×12 board, the smallest square board on which a tour is possible. It is equivalent to a fiveleaper tour on a serrated board formed by 45 degree rotation of the cells of one colour.
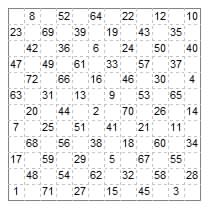
H. J. R. Murray (1917) in his article on knight tours on the half-board in the British Chess Magazine mentions six tours formed by joining two semi-magic 4×8 tours so that they add to 260 in the files and to 132 in the upper ranks and to 388 in the lower ranks (examples had previously been given by Brede and Wenzelides). He writes: "The two which I diagram could on a cylindrical board in which the upper and lower edges were contiguous be renumbered to give a magic tour". The linking knight move across the cylinder join is in effect a {2,7} leap.
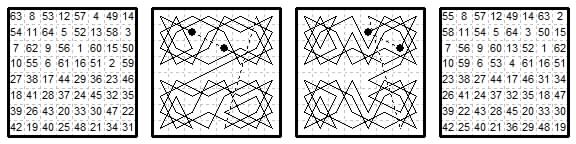
8×8. (Jelliss 19 Dec 1990). This consists of simple boustrophedonal tours of the four dabbaba domains, joined together by crossboard links.
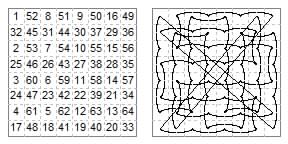
The {6,7} = root-85 mover is a freeleaper on a sufficiently large board, but not on the 8×8 board, so this combination can be regarded as an 'amphibian' on this board.
14×14. In Chessics (#24 1985 p.93) I gave a closed centrosymmetric tour on this board. Only the first half of the tour is shown in numerical form here. The rest, 99 to 196, rotates the first part 180 degrees (diametrally opposite numbers differ by 98). Part of the route (1 to 42) is shown to illustrate the system of construction; the route 99 to 140 is similar. This is a combination of two pieces that are freeleapers on a sufficiently large board.
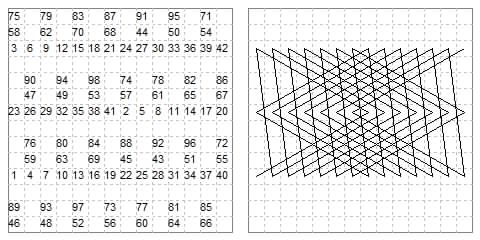
10×:10. In PFCS (Jun 1932 prob 404 a/b) W. E. Lester gave a shortest closed path of 8 moves, and E.J.van den Berg gave a longest closed path on 10×10 of 40 moves.
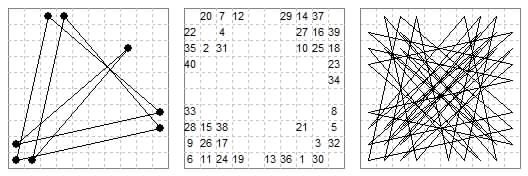
Bison Cryptotour Puzzle. Camel + Zebra = Bison. ANSWER.
"If in chess you may chance to set eyes on
Some camels with black and white stripes on
Or zebras with humps making camellar jumps
You've seen bison, or bisons, go by son!"