
The simplest move on a board of squares is the {0,1} step of the wazir or single-step rook. The wazir's move takes it through the sides of the square on which it stands. On a chequered board this is a step to any adjacent square of opposite colour. Since the wazir does not participate in modern chess, other than as a component in the moves of king, queen, rook and pawns, its study has been unjustly neglected.
Wazir tours, besides being of interest in themselves, are also useful in analysing the structure of knight's tours on boards whose sides are double those of the wazir tour (see under Magic Knight's Tours – Braid Method).
The general problem of enumerating wazir tours on rectangular boards, one would think should not be intractable to normal mathematical methods, such as the derivation of recurrence relations, but as far as I know it has only so far been tackled successfuly in a few special cases.
The shortest wazir paths equivalent to an (m,n) move obviously use m + n moves. The number of shortest wazir paths equivalent to an (m,n) move is thus (m+n)!/m!n!.
A closed wazir tour is possible on any rectangular board of an even number of cells and with sides greater than one. The area enclosed by any closed wazir tour on the m×n board is (mn/2) − 1. For square boards this sequence runs 1, 7, 17, 31, 49, 71, 97, 127, 161, 199, ... The shapes outlined by the tours are of course 'polyominoes'.
Obviously a wazir can make only one geometrically distinct open tour on a board of 1×n cells; a straight walk from end to end.
On a board 2×n (n>1) the wazir has one closed tour; a walk around the edges. The numbers of 2×n wazir open tours are tabulated below. The figures for G(n) were first found by drawing out the tours for the cases 2 to 6, then deducing the general formula and using it to calculate the other cases. The diagrams show the tours of these smaller boards, listed systematically:

In drawing the tours we find there are (when n>2) n with an end at a corner, then n–3 with an end one in from a corner, then n–5 with an end two in from a corner, and so on, until we reach 1 or 2 as last term. Thus G(n) = 1 + (1 + 3 + 5 + ... + (n–1)) when n is even, and 1 + (2 + 4 + 6 + ... + (n–1)) when n is odd. Denoting by h and k the nearest whole numbers such that h£ (n/2) £ k, and using the properties that the sum of the first s successive odd numbers is s^2 and the sum of the first s even numbers is s(s+1) we have G(n) = 1 + (n/2)^2 or 1 + [(n–1)/2][(n+1)/2], which can be expressed concisely as G(n) = 1 + hk. For n = 1, 2, ... the successive values are: 1, 2, 3, 5, 7, 10, 13, 17, 21, 26, 31, 37, 43 50, 57, 65 ... from this formula. However for n = 2, when the board is square the 2 reduces to 1 due to rotation being possible.
The S(n) symmetric tours consist of one U-shaped tour with both ends in the first rank (as oriented in the diagrams above) and a lengthwise axis of symmetry and when n is even (and > 2) there are n/2 others that have a breadthwise axis, but when n is odd there are instead (n−1)/2 that have 180° rotational symmetry. Thus S(n) = h + 1. The successive values for n = 1, 2, ... are: 1, 2, 2, 3, 3, 4, 4, ... but again for n = 2 we must reduce this to 1. A curiosity of the 2×n case is that if the two end-points of a wazir tour are symmetrically placed then the tour itself must be symmetric, and when it exists it is uniquely determined. It happens that the number of reentrant tours equals S(n); this set includes the U-shaped tour and one other symmetric tour when n is even. The total of tour diagrams can now be calculated by the usual formula for rectangles: T(n) = 4G(n) – 2S(n) = 4hk − 2h + 2. The successive values are: 1, 1, 8, 14, 22, 32, 44, 58, 74, 92, 112, 134, 158, 184, 212, 242, ...
For a closed tour n must be even. Every 3×2m closed wazir tour forms a circuit round the edge with m−1 'indentations', each of which may be in either of the longer edges (2 choices). The number of tour diagrams is thus T(n) = 2^(m−1). Diagrams of the first few cases follow.
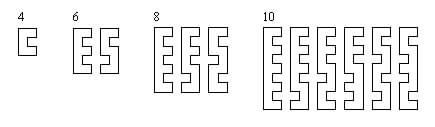
To find the number of symmetric tours we separate the cases of m even and odd. When m is even a tour can always be oriented with the middle indentation in a chosen edge. Then there are 2^(m/2 − 1) ways of indenting on each side of this, giving this number of tours with an axis of symmetry. When m is odd there is no central indentation, but we can always reflect if necessary so that the first indentation is in the chosen edge. The other indentations in that half can be made in 2^((m−1)/2 − 1) ways, giving this number of reflective and the same number of rotative tours. Thus S(n) = 2^(g−1) where g is the nearest whole number g³n/4. We can now calculate G(n) = T(n)/4 + S(n)/2 = 2^(m−3) + 2^(g−2).
Table of results:
n = 4 6 8 10 12 14 16 18 20 22 24 G(n) = 1 2 3 6 10 20 36 72 136 272 528 S(n) = 1 2 2 4 4 8 8 16 16 32 32 T(n) = 2 4 8 16 32 64 128 256 512 1024 2048
The following diagrams show the first few cases of open tours 3×n. They are grouped according to the separation of their end-points. Symmetric tours are printed with a heavier line. I have the following limited results: 3×3: G = 3, S = 1 (rotary), T = 20. 3×4: G = 19 (7 reentrant), S = 7 (4 axial, 3 rotary), T = 62. 3×5: G = 36, S = 6 (rotary), T = 132. 3×6: G = 91 (19 reentrant), S = 14 (8 axial, 6 rotary), T = 336.

The two wazir closed tours on the 4×4 in the shape of H and C (hot and cold) are well known.
More generally, there are 38 geometrically distinct open tours 4×4, of which 14 are reentrant (9 from the C tour and 5 from the H) and 7 are symmetric.

The seven axially symmetric tours, when numbered and arranged with the axis vertical, result in semimagic tours, that is with the ranks all adding to the magic constant 34, since each rank consists of two pairs of complements adding to 17. The sums of the files and diagonals vary, none add to the magic constant.
01 02 15 16 04 03 14 13 05 08 09 12 06 07 10 11 |
01 08 09 16 02 07 10 15 03 06 11 14 04 05 12 13 |
02 01 16 15 03 04 13 14 06 05 12 13 07 08 09 10 |
02 01 16 15 03 08 09 14 04 07 10 13 05 06 11 12 |
02 03 14 15 01 04 13 16 06 05 12 11 07 08 09 10 |
03 02 15 14 04 01 16 13 05 08 09 12 06 07 10 11 |
07 08 09 10 06 01 16 11 05 02 15 12 04 03 14 13 |
A recurrence relation for T(n) in this case was given by C. Flye Sainte-Marie (L'Intermédiaire des Mathematiciens, vol.11, 1904, pp. 86-88) namely: T(n) = 2T(n−1) + 2T(n−2) − 2T(n−3) + T(n−4), with initial values T(1) = 0, T(2) = 1, T(3) = 2, T(4) = 6. Diagrams of the geometrically distinct cases for 4×5, 4×6, 4×7 and 4×8 follow, with symmetric tours in bold line. Results summary: 4×4: G = 2, S = 2 (1 biaxial, 1 axial), T = 6. 4×5: G = 5, S = 3 (axial), T = 14. 4×6: G = 15, S = 10 (3 biaxial, 6 axial, 1 rotary), T = 37. 4×7: G = 26, S = 6 (axial), T = 92. 4×8: G = 72, S = 24 (4 biaxial, 16 axial, 4 rotary), T = 236.

On the 5×6 board there are 44 closed tours, 11 symmetric (7 axial, 4 rotary), 33 asymmetric.

On the 5×8 board I find 440 closed tours (count not checked). These may be classified by corner patterns, and include 34 symmetric tours, as shown below.

In enumerating these I classified the edge-formations according to number of indents, 0, 1, 2. The tours can then be classified as 0001=13, 0011=17, 0012=12, 0101=13, 0102=13, 0202=5, 0111=27, 0112=18, 0121=9, 0212=4, 1111=10, 1112=6, 1212=2. The single indents can be subclassified as central and offset. Total 149 closed tours. Of these 28 are symmetric (1 birotary, 5 rotary, 3 biaxial, 19 axial).

And there are 121 asymmetric:

Classification by various features: Straight edges: 0=18, 1=58, 2=60 (29 adjacent, 31 opposite), 3=13. Indents: 1=9, 2=34, 3=52, 4=42, 5=10, 6=2. Cut-away centre = 34.
On the standard chessboard my latest count of the wazir tours with 180° rotation (6 June 2004) found 374, of which none have 90° rotary symmetry but 20 (shown here) are biaxial. A previous count missed the sixth diagram shown here.

Wazir tours in quaternary symmetry total 224 reflective, 101 rotative (these totals not checked). The reflective cases can be classified according to the distance in from the edges of the moves that cross the two axes, thus: (0, 0) 52, (0, 2) 38, (0, 4) 86, (2, 2) 14, (2, 4) 34. I show one example from each class, and some assorted rotative examples.
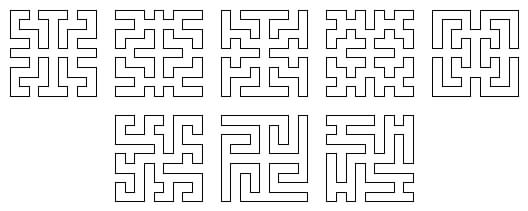
The 4×4 H-pattern can be repeated in 2×2 array and the four components joined up by an H-pattern of linkages to generate a quaternary reflective tour 8×8. This in turn can be used to generate a tour a factor of 2 larger, that is 16×16 as shown in (A) below, and the process can be continued to larger boards. More variety in the pattern can be obtained by making the joining H-connections horizontally instead of vertically as in (B).
Similarly, the 6×6 swastika pattern can be repeated in 3×3 array and the nine components joined up by a swastika pattern of linkages to generate a quaternary rotative tour on the 18×18 board, as in (C) below. This in turn can be used to generate a tour a factor of 3 larger, that is 54×54, and so on. Alternatively the anti-clockwise swastikas can be joined clockwise as in (D). Many varied patterns of this type can be constructed by systematic linking of tours. The reader is invited to try out this visually constructive recreation.

Tours of this type are similar to patterns encountered in the study of 'fractals' or 'space-filling curves'.
In the 2×2 wazir tour, numbered 1 to 4, it so happens that the square numbers, 1 and 4, are in the same row. This may seem a trivial observation, but when we try to extend the feat to larger boards it begins to appear much more interesting. The feat of having all the square numbers in a row cannot be accomplished on boards of side 3, 4 or 5, but when we consider side 6 it turns out to be possible once more, and moreover the solution is unique!

The 2×2 case must form the basis for any larger tour with the squares in a row property. To get the next square, 9, in line with the 1 and 4 there are three ways but only the method for the 6×6 board extends to larger square boards of side 10, 14 and so on, but the routes on these larger boards are not completely determinate - an alternative corner route for the 10 case is shown.
This result obviously has some connection with the fact that the differences of successive squares are successive odd numbers - an elementary result of number theory. The number of cells to be visited by the wazir between z2 and (z+1)2 is 2z and these must all lie on the same side of the row of square numbers.
[A version of this item was first published in Chessics (#21 p.56 1985), with the alternative route noted in G&PJournal (#8+9 p.143 1988-9).]
Some other simple figured tours left as an exercise: 4×4 wazir tours showing (a) squares at corners of a square, (b) squares at corners of an oblong also appeared in G&PJournal (#11 p.178 1989).
In 1978 I came across some amusing chess puzzles by T. R. Dawson involving rook journeys and knight tours on the vacant squares of a board on which eight white queens are standing in one of their famous twelve mutually non-guarding positions. These compositions set me wondering whether a closed non-intersecting rook tour (i.e. a wazir tour) was possible on the 56 unobstructed squares. I quickly found that a symmetrical tour around the symmetrically arranged queens is possible, as shown in diagram A. In fact 14 such symmetrical tours (and about 150 asymmetrical ones) are possible round this particular setting of the queens. Of the other 11 solutions to the 8Qs problem nine do not admit of any wazir cruise around the queens. The arrangement shown in B allows just 20 different tours. The remaining case C however provided a surprise, since the tour is in this case uniquely determined!
To to see the uniqueness of this tour: draw the 8Q position on a blank diagram, then draw in the wazir moves in stages, considering the squares in the following order: (1) a12358, b1, c8, d1, e8, f1, g8, h12468; (2) b7, c2, d7, g27; (3) a6, b3, e2, f7, g5; (4) c6, f6, g3; (5) b5, c5, e6, f3; (6) c34, e5, f5; (7) de34. Throughout the process you must take care not to form a closed path covering only some of the vacant squares and not all. Within each stage the cells listed can be examined in any order.

This discovery naturally led me to enquire if the number of blocks needed to fix the wazir tour could be reduced. The number of blocks must be even, since the wazir moves alternately to black and white squares, so in a closed tour there must be the same number of each. The number was quickly reduced to six (a6, c2, d6, e6, f2, h6). Then further search led to the unexpected discovery (February 1978) that four blocks suitably placed on the chessboard are sufficient to determine a unique closed wazir tour of the remaining squares. These results were published in The Problemist [vol.10, nr.22 (xi 1979) p.376]. Three four-block arrangements were reported there. In 1981 Tom Marlow sent me seven more solutions, which stimulated me to find four more, and these were published in Chessics [vol.1, nr 12 (1981) pp.7-9, 12-13]. The 14 known solutions are as follows. The last one shown is the only one with a block within the central 4×4.

THEOREM: On the 8×8 board the minimum number of blocks to force a unique closed wazir tour of the remaining cells is four, and one block must appear in each quarter of the board.
Proof: [Chessics 1981] If there are only two blocks then at least one 4×4 quarter of the board must be free of blocks. We can take it to be the a1 quarter. Now consider the 3×3 cells in the a1 corner, and all possible routes of the wazir through these nine cells. The following diagrams show the possible paths.

Diagrams 1-2, 3-4, 5-6, 7-8, 9-10, 11-12, 13-14, 15-16 are pairs in which the entrances and exits to the 3×3 are the same but the routes followed are different; in other words the tour is not uniquely determined in these cases. Diagram 17 similarly pairs with its own reflection in the a1-d4 diagonal. Finally diagram 18 can be settled by considering how the wazir tour outside the 3×3 must link up the entrances and exits to the 3×3 without crossing over or forming detached circuits. The connections must be either a4-b4, c4-d1, d2-d3 or a4-d3, c4-d4, d1-d2. If we now delete the interior of the 3×3 we can reconnect in accord with pattern 3, or its diagonal reflection. QED.
The general problem is: How few blocks are needed on a board m×n so that there is a uniquely determined closed wazir tour of the remaining cells? On the larger boards it is as if the blocks direct the wazir across the open board in lateral or diagonal zigzagging 'wazir waves'. No blocks are needed on boards 2×n. One block suffices on boards 3×3 and 3×5. Two blocks suffice on all boards 4×n, e.g. on any board 4×2m a solution is (a1, y2), where y represents the penultimate file. Two blocks also solve boards 3×4, 3×6, 3×8. Three blocks are needed on boards 3×7, 3×9, 3×11. Four blocks on 3×10, 5×6, 6×6, 8×8, and generally 8×2m, e.g. (a3, c6, y2, y6). Five on 7×7, six on 12×12, seven on 9×9, eight on 10×10, 14×14, 16×16; nine on 11×11. T. H. Willcocks considered the problem for larger boards and gave some examples in which larger solutions are derived from smaller ones.
The difficult 10×15 case appeared in the Journal of Recreational Mathematics 1999 and I was able to solve it in 8 blocks as shown below.

There are one or two subtle points: (1) Put in all the obviously forced edge moves, shown by heavy lines in the second diagram, then b2-b3 is forced, since b2-b1 results in c2-c1-d1 and no move through d2. (2) When the forced 'staircase' moves are put in, then b6-b7 must be taken, since a6-c6 and a7-c7 close off short circuits. Then a6-a7 is barred since it forces b6-c6 and b7-c7 which creates a longer short circuit. Putting in a6-b6 and a7-b7, there is a 'mini-avalanche' forcing c6-e6 and c7-e7, then f6-g6 and f7-g7. (3) Now there are more forced staircase moves, leading to a similar situation: o8-o9 is barred; instead o8-n8 and o9-n9 must be inserted, leading to a mini-avalanche in the opposite direction.
A snake on a square-array board is a wazir path in which every two successive moves are at right angles, and no square is ever re-entered. Any such path is, like a snake, considered to have a head, where the wazir stops, and a tail, where it starts. The question considered here is: How many different shapes of snake are there of length n wazir moves?
A partial analysis, giving an estimate for the required enumeration, runs as follows. There is one snake shape of length 1, and there is one snake shape of length 2. We can always rotate or reflect a snake of length 2 or more so that it "stands on its tail, facing right", i.e. its two tail segments go to the right and then upwards. There are two snake shapes of length 3. From their shapes we can call them C and S. There are three snake shapes of length 4. We diagram all these cases:

We now note that one 4-segment snake is an extension of the C-snake and that the other two derive from the S-snake. Furthermore, the C-snake produces a snake with an S-shaped head end, while the S-snake produces one S-headed and one C-headed snake. Denote the number of snakes of length n (greater than 2) by T(n) and the number that are C-headed by C(n) and the number S-headed by S(n), so that
T(n) = C(n) + S(n) ..........(1)
If we take the rules for propagation of snakes derived from the above simple examples as applying generally, then they imply that:
T(n+1) = C(n) + 2S(n) ..........(2)
S(n+1) = C(n) + S(n) ..........(3)
C(n+1) = S(n) ..........(4)
Putting n−1 for n in (3) we find S(n) = C(n−1) + S(n−1) = T(n−1) by (1) and hence:
T(n+1) = T(n) + T(n−1) ..........(5)
This is a recurrence relation for calculating values of T from earlier values of T, and since the first two values of the required sequence are both 1, we conclude that T(n) is the Fibonacci sequence:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
The above analysis works perfectly until we get to length 12, in which case we find that the total number of snake shapes is not 144 but 141. The Fibonacci rule breaks down at this stage because in three cases, illustrated below, the head of the snake encounters its tail, which prevents further growth or reduces the choice of directions for the next wazir move from two to one.
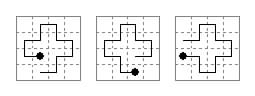
Can anyone modify the rule to extend it to apply to snakes of greater length?
[A version of the above article first appeared in QARCH (Vol.1, No.9) a newsletter of the Archimedeans (the Cambridge University Mathematical Society) dated March 1987.]