Tours with rotary symmetry are those invariant to 180 degree rotation but not to 90 degree rotation, nor to any reflection. In the case of open tours there may be a central cell, with two knight moves passing through in a straight line, in which case the board will have an odd number of cells. Alternatively the board may have an even number of cells, and there will be a central knight move passing across the centre point, which will be the mid-point of a side were two cells meet. Since a knight tour cannot cross a diagonal or lateral line at right angles, open tours with axial symmetry must meet the axis at a cell centre, and therefore use an odd number of cells. The assortment of tours shown here is not the result of any particularly systematic study, just an accumulation of various special cases. For examples on less than 16 cells see the page on Open Tours on Small Boards.
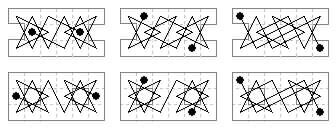
16 cells. The six rotary tours on the untourable 3×6 board, omitting two cells, listed by Andrew Usher [2022]. Previously we showed only the first two.

17 cells. Here are some shaped boards with open tours showing lateral axial symmetry.
The 3×5 with a cell added at the middle of each long edge has rotary tours.

18 cells. The following examples are tours on the 4×5 board with two corner cells omitted. There are 18 symmetric open tours (including two reentrant cases derived from a Bergholtian closed tour).
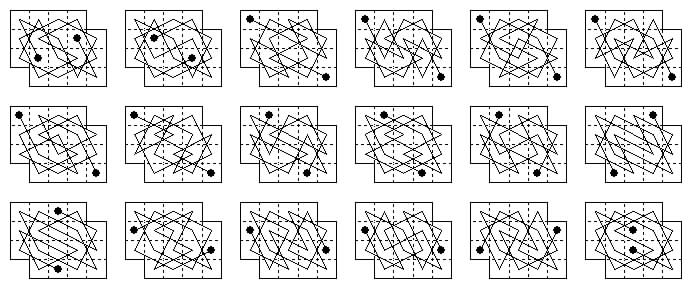
19 cells. The board formed of the 3×5 with a cell added at the middle of each edge has no tours for the same reason as the 3×5 board: formation of a short circuit b2-d2-f2-d4 on the minority colour. However if the end cells are moved next to the side cells to form a board with rotary symmetry many tours become possible, in fact 62, made up of 16 b3-d3, 14 a2-e4, 14 a4-e2, 12 b5-d1, 6 c4-c2 (Jelliss Feb 2018). In these rhe nine even numbers form a diagonal square, and in the six cases shown below this is a magic square! This research was stimulated by an 8×8 figured tour by T. R. Dawson (Vie Riennaise 1932) incorporating a magic square, so I wonder if the result is new.

Six further examples from the 62 are diagrammed.

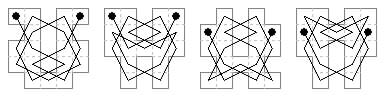
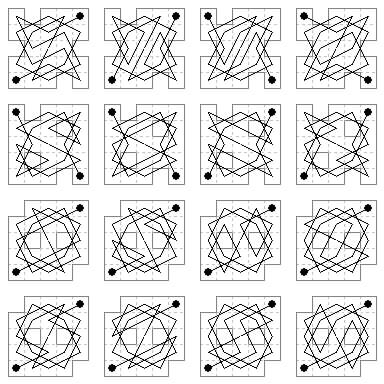
21 cells. Tourable centrosymmetric boards of 21 cells can be formed from the 5×5 with four cells removed at various places, but this does not include the board with the four corners removed, since when chequered it has 12 of one shade and 9 of the other. There are five ways of removing two of each shade that will admit rotary symmetric open tours. I have a note that the number of tours of each shape is: 44, 44, 4, 4, 8. Total 104. This enumeration has not been independently checked. Diagrams follow.
case 1
case 2

cases 3, 4, 5.
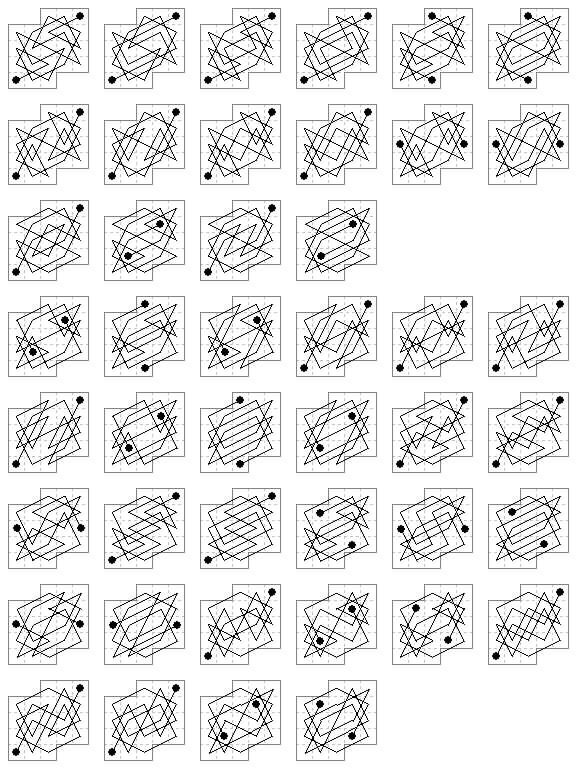
23 cells. Although on the 5×5 board there are only 8 symmetric open tours, all corner to opposite corner, by removing two opposite corner cells we now find 36 symmetric tours. The 8 with ends b3-d3 correspond to the 5×5 cases, but there are also 14 each with ends a4-e2 and a2-e4. We show two of each of these cases.

23 and 25 cells. Some just-connected open tours with lateral axis; one of 22 moves on 23 cells, two of 24 moves on a board of 25 cells. Other moves can be added, e.g. in the second b3-d2-f3 making a Murraian closed tour on 26 cells.
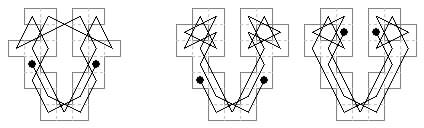
28 cells. In the pages on rectangular boards we prove there are no symmetric open tours on the 5×6 board. Since a symmetric open tour is possible on the 3×4 board, which is the middle area of the 5×6 board, this is perhaps surprising. Tours of this type are however possible by omitting a pair of corner cells. Here are six examples, out of 82 I found, one for each selection of one, three or five 'inner' moves.
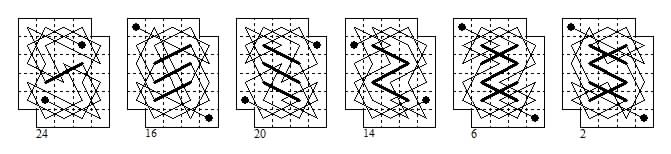
This amusing 'leotard' board has rotary symmetry but only has 5 symmetric open tours. The first two are from L'Echiquier Feb 1929 where they are attributed to Vatriquant, Post and Deprez, independently. The other three I found (2015).
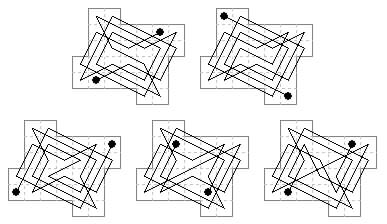
29 cells. Showing the five possible end-positions in an 'oval' shaped board.
And rotative open tours of two other board-shapes Suitable boards must have 15 cells of one colour and 14 of the other when chequered.
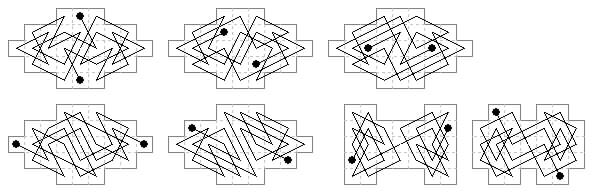
31 cells. The shape of two 4×4s overlapping at a corner, has tours with diagonal axis (three examples shown) but none centrosymmetric. There are also asymmetric tours (not shown).

A centrosymmetric tour of overlapping 3×6 boards is shown here.

The serrated board below has two diagonal axes of symmetry, and when chequered consists of 3×5 and 4×4 diagonal arrangements intermeshed. The 4 distinct end-positions are shown.
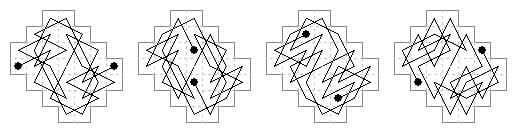
32 cells. A 5×6 board with two attached cells. The first open tour shown here is by Post (L'Echiquier Mar 1929), the second on the same board (Jelliss (1999) has the middle move in a different direction.

37 cells. The octonary 37-cell solitaire board has no knight tour since when chequered the colours are in the ratio 16 to 21. In these assorted boards the ratio is the required 18 to 19.
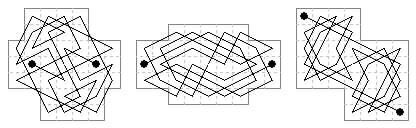
39 cells. Two open tours (Jelliss 2017).
41 cells. Two open rotary tours on boards with biaxial and birotary shapes (Jelliss).
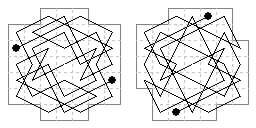
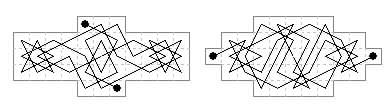
43-cells. Two centrosymmetric examples with different board shapes.
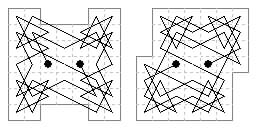
47 cells. Two centrosymmetric examples on cross-like boards.
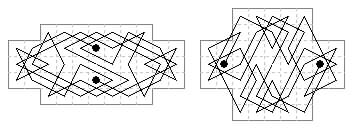
49 cells. A shaped 49-cell board is that consisting of two 5×5 boards overlapping at a corner. A corner to centre tour on each part can join to give both axial and centrosymmetric open tours (unlike the similar 31-cell board where centrosymmetry is impossible) [not diagrammed]
51 cells. A symmetric open tour on a serrated lozenge shape.
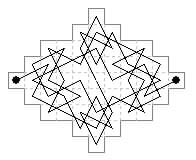
53 cells. Three centrosymmetric open tours on assorted board shapes.
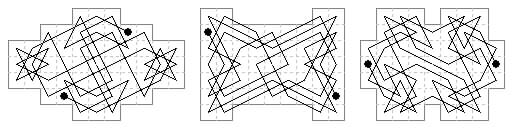
59 cells. Centrosymmetric open tour on a shaped 59-cell board (7×9 - 4).
61 cells. Two centrosymmetric open tours on 61-cell shaped boards (7×7 + 12).
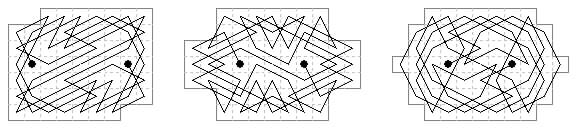
73 cells. An open symmetric 73-cell tour from L'Echiquier Jan 1927 (prob.161).
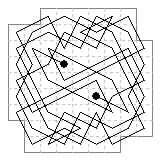
This was used as a cryptotour spelling a quotation from Gauss: "La mathematique est la reine des sciences et l'arithmetique la reine des mathematiques" one letter to a cell.