
This page has been updated (June 2022) to include a new enumeration by Andrew Usher of symmetric closed tours of 14 cells. Closed tours have been completely enumerated (including asymmetric cases) only on boards up to 12 cells. To keep the enumerations within bounds it is necessary to restrict the study to symmetric cases or to tours within compact frames.
The diagrams are arranged according to the size of the containing rectangle, oriented with the longer side (if any) horizontal. Boards with two or more tours are linked to indicate they are the same shape.
The mediaeval manuscripts contain the puzzle of the four knights, often attributed to the later writer Guarini (1512), where white and black knights placed in the corners of the 3×3 board are to be interchanged. The knights go in procession round the star-shaped closed tour of the eight edge squares. The 3×3 closed tour is the first example of a tour with octonary symmetry.


Four of the Vinje tours are symmetric, one each of the Bergholtian, Murraian, Sulian and Eulerian types. The Bergholtian tour, on an H-shaped board, has biaxial symmetry (also known as direct quaternary symmetry with lateral axes) and can be regarded as having Murraian symmetry about the axis with two cells and Sulian symmetry about the other axis.
T. W. Marlow (1995) has noted that there are six further 10-ominoes with holes that have closed knight tours, to be addded to Vinje's enumeration.

In the remarkable collage that follows, the shaped boards are fitted together within a 13×13 area to form a larger board, also without holes, in which the tours join together, with deletion of one move in each, to form a closed tour of the composite board. This is due to A. W. Baillie (Fairy Chess Review, problem 8531 November 1949 p.84 and June 1950 p.110). The symmetric cases are included.
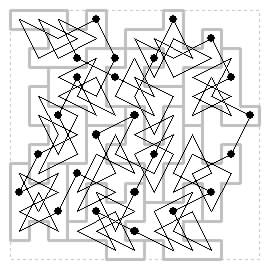
Enumeration of the 12-cell boards with closed knight tours has proved to be a considerably stiffer problem than for the 10-cell case.
I sent a summary of my results to Tom Marlow (27 October 1995) writing: "I think I have found all those up to 4×5 minimum containing rectangle, by a process of systematically removing squares from the rectangle, while ensuring the tourability of the remainder. However, for the larger sizes this method becomes inefficient. The 4×6 cases have mostly been found by 'folding out' a pair of moves from the 4×5 cases, and permuting the different shapes removed from the corners. The 5×5 cases, which I'm sure are very incomplete, resulted mostly from an examination of 12-cell tours that include a 2×3 rectangle. The 5×6 was 'folded out' from a 4×6 case. The particularly nice 6×6, where there seems to be the only one solution, was found by pure intuition before I started the systematic count. I haven't proved to my satisfaction that no cases with a dimension greater than 6 can occur, but this seems probable."
Mr Marlow responded (24 November 1995): "I am finding the polyomino tour problem quite addictive." He gave the 10-cell tours with holes as diagrammed above and diagrams of nineteen 12-cell boards (with 24 tours) not included in my list. He wrote: "My method has been to start from the opposite direction to you and look for 12 step knight loops within a rectangle. Then I see if the squares form a connected shape and reach to all edges. I found that I could easily adapt a magic tour computer programme to search for 12 step loops and then worked by hand. It seems clear that neither dimension can be greater than six."
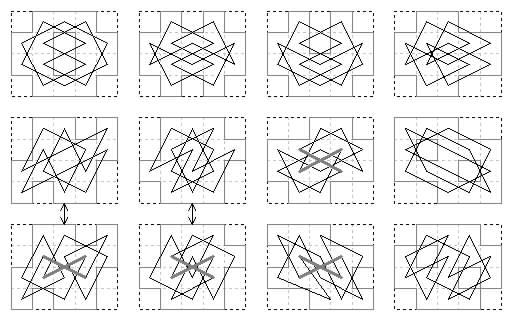
We now give diagrams of all the symmetric closed tours of 12 cells. There are 17 on shaped boards. There are two 12-cell tours with quaternary symmetry, both of the type with two diagonal axes. The one within the 4×4 frame was found by Euler (1759), the one within the 6×6 is my own discovery.

There are nine other closed tours of 12 cells with centrosymmetry (i.e. 180 degree rotational symmetry). Of these, 3 are Eulerian (i.e. not passing through the centre) all within the 4×6 frame (two being on the same board shape). The other 6 are Bergholtian (i.e. passing through the centre), one within the 3×6 frame and five within the 4×5 frame. The remaining six have a single axis of symmetry with diagonal axis within a 5×5 frame.
There are 8 holey boards with symmetric tours (two with two symmetric tours). One tour in the 5×5 frame has centrosymmetry (Eulerian). One tour 4×5 has a lateral axis (with Murraian symmetry). The other 8 tours have a diagonal axis (Murraian), four 4×4 and four 5×5. The first 4×4 tour here was shown by Murray.

The first and last of these boards have a symmetric tour (see above) as well as the asymmetric one. The others have no symmetric tours, only the one asymmetric tour. We are counting 'geometrically distinct' tours here. Each of these tours can be seen in an alternative orientation by rotating the first two boards or reflecting the others. The two examples with lateral axis differ only in having a pair of moves, and the associated cell, folded up or down.

3×5, 3×6 and 4×4 cases.

4×5 case shaped. (a) asymmetric boards with multiple tours: 4 with 3 tours, 5 with 2 tours.
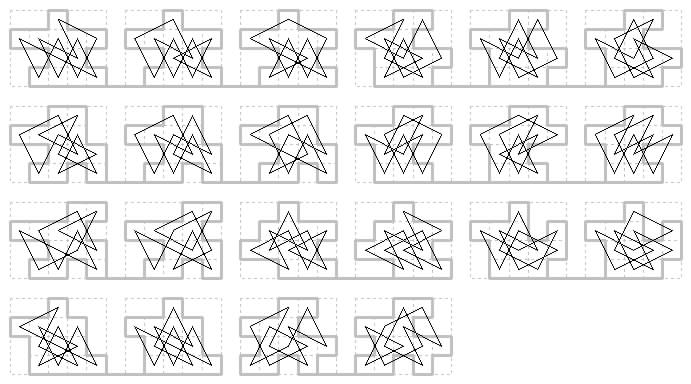
4×5 case shaped. (b) asymmetric boards with 1 tour and incomplete middle file. The sixth is the only example where one of the centre two cells is cut away.

4×5 case shaped. (c) asymmetric boards with 1 tour and complete middle file.

4×5 case holey. (a) asymmetric with multiple tours. We show one shape with four tours, then three shapes with two tours each.

4×5 case holey. (b) Asymmetric boards with a single tour.

4×6 case shaped. We begin with two shapes that have two tours each. The other ten have a single tour.

4×6 case with holes. 8 boards with 10 tours. Two boards with two tours. Six with single tours.

5×5 case shaped. (a) asymmetric boards with multiple tours: there is one with six tours, one with three,

and five with two.

5×5 case shaped. (b) asymmetric boards with single tour: 11 with no complete rank or file. The third one includes three two-move knight lines and also cycles round in one consistent direction.

5×5 case shaped. (c) asymmetric with single tour: 18 with complete rank but no complete file

5×5 case shaped. (d) asymmetric with single tour: 8 with complete rank and file.

5×5 case holey.. One example with four tours. Ten with single tour.
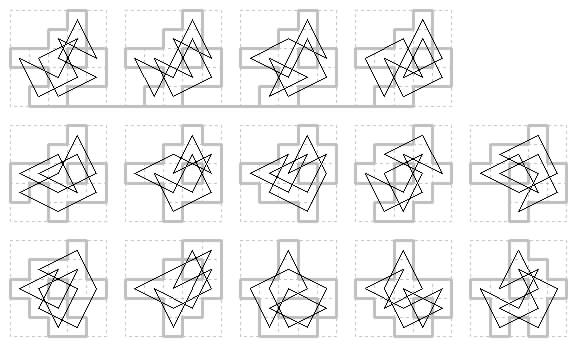
5×6 case. Three shaped boards. Two holey boards, one with two tours.

| Frame size | Boards | Tours | Symmetric | With hole |
| 3×5 | 1 | 1 | 0 | 0 |
| 3×6 | 2 | 2 | 1 | 0 |
| 4×4 | 9 | 13 | 3B/5T | 2B/4T |
| 4×5 | 83 | 103 | 8B/6T | 30B/36T |
| 4×6 | 22 | 27 | 2B/3T | 8B/10T |
| 5×5 | 67 | 83 | 12B/11T | 16B/19T |
| 5×6 | 5 | 6 | 0 | 2B/3T |
| 6×6 | 1 | 1 | 1 | 0 |
| Totals | 190 | 236 | 27B/27T | 58B/72T |
Thus for example within the 4×5 frame there are 83 different 12-cell boards, of which 30 have a hole. Since some of these can be toured in two or more ways they give 103 tours, (36 on holey boards and thus 67 on shaped boards). There are 8 symmetric boards of this size but only 6 symmetric tours since two of the symmetric boards only have asymmetric tours (another has two tours, but only one of them is symmetric).
In the 5×5 frame there are 12 symmetric boards but one of these, the one with lateral axis of symmetry, has only an asymmetric tour, so there are only 11 symmetric tours. Again, one of the symmetric boards has two tours but only one of these is symmetric.
As noted at the start of this study, in course of doing the diagrams I found three errors. A 4×4 board claimed to have a tour only had a pseudotour. A 4×5 board marked as having 2 tours only had one. A 5×5 board marked as having one tour in fact had two. I hope the totals are now correct!
THEOREM: A 12-cell closed tour cannot have an enclosing rectangle of side greater than six.
Proof (sketch): Each edge must contain at least one cell that is part of the tour, with two cells reachable from it (say a3, b5, c4
or a3, c2, c4), and at least two other cells (say b3, b4 or b3, c3) to connect these. These in turn generate two other cells each, but it will be
found that none can coincide with the previous five. Two such batches of nine against opposite edges separated by seven units must have an overlap
of at least six to give a 12-cell tour (3 + 6 + 3), since an overlap of 5 uses 13 (4 + 5 + 4) and of 4 uses 14 (5 + 4 + 5). The only possible
arrangements to do this result in lozenge-shaped short circuits of four moves. (For example a3, b3, c2, c3, c4, d2, d4, e2, e3, e4, f3, g3.)
The following enumeration of 14-cell closed symmetric tours by Andrew Usher was sent to us in May 2022. He finds 58 tours of this type.
4×4 frame with two cells omitted. One board shape with two axial tours of Sulian type. There is also a unique asymmetric solution.
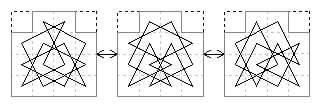
3×6 frame with four cells omitted. Five boards. Five tours.
One biaxial tour. Two axial tours (Sulian type). Two rotary tours (Eulerian type).
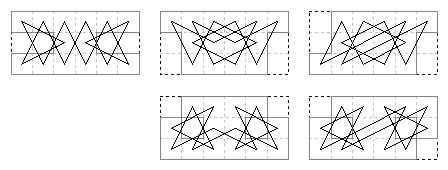
4×5 frame with 6 cells omitted. Ten boards with twelve tours.
Two tours biaxial. Two tours lateral, one Murraian and one Sulian.
Eight tours rotary, four Eulerian and four Bergholtian.
The two boards with two tours have one of each type.
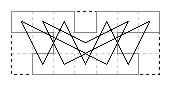
3×7 frame with 7 cells omitted. One board with one tour, Murraian lateral.
4×6 frame with 10 cells omitted. Six board shapes with 8 tours, all Sulian.
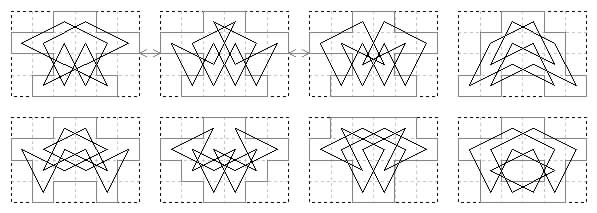
5×5 frame with 11 cells omitted. Three board shapes. Five tours, all Murraian lateral.

4×7 frame with 14 cells omitted. Seven board shapes and 7 tours.
Two Murraian lateral, Four Bergholtian, One Eulerian.
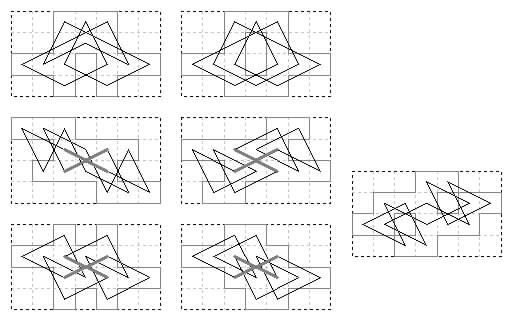
5×6 frame with 16 cells omitted. 14 board shapes with 17 tours.
Seven Bergholtian. Nine Eulerian. One Murraian lateral.
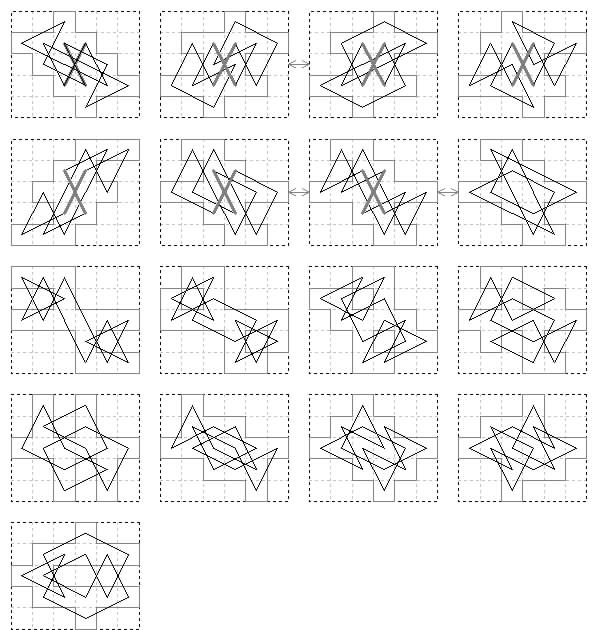
5×7 frame with 21 cells omitted. One board with one tour. Murraian lateral.
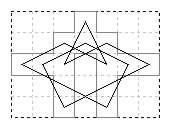
Total 58 symmetric tours.
14 cell asymmetric tours. There are of course also many asymmetric 14-cell tours. See the 4×4 frame above for one example.
Andrew gives these three tours possible within the 3×6 frame with four cells omitted.

Tours on 16 or more cells are shown on other pages, classified according to the symmetry they show.