
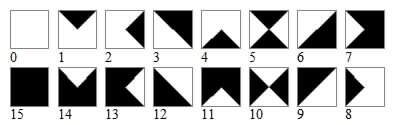
Many patterns can be formed by square tiles divided into black and white halves by a single diagonal. These tiles then being fitted together in a square lattice with their edges matching in color, white to white or black to black. A single tile has four orientations.
There are eight ways of maching a pair of tiles, forming a triangle or stripe where they join. Combining these in matching pairs gives sixteen possible 2x2 arrays. These form patterns of four types: 8 chevrons, 4 stripes, 2 squares and 2 X-crosses

Also shown above is a selection of 4x4 patterns formed according to the rules. Of course many other patterns can be formed if the matching rule is abandoned.
Two diagonals divide the square into triangular quarters. The edges, or the triangular quarters, of a square tile can be coloured with two colours in 2^4 = 16 ways.
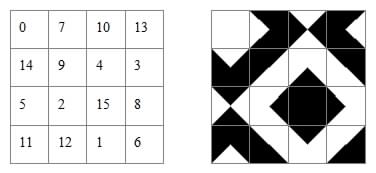
Stanley Collings in his Puzzle Column in the IMA Bulletin January-February 1985 p>29 noted that "any integer from 0 to 15 in a sense has four digits in the binary code, and so is representable by a quartered tile in which each quadrant is black or white (black denoting 1 and white 0). Taking the qiuadrants clockwise from the top gives the numbering shown.
He then gives an example of a 4x4 magic square, numbered 0 to 15, reprsented by numbers in this graphical form, which has the colours of the tiles match where their edges meet.
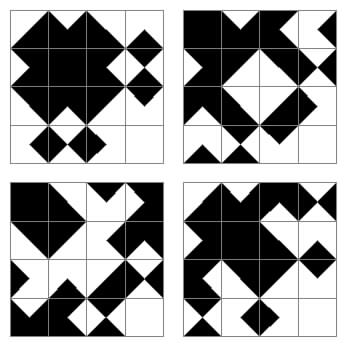
I have a note of four other 4x4 patterns formed by placing the tiles together with matching edges. The first of these occurs in one corner of the 9x9 three-colour problem noted below.
Using three colours 81 tiles can be produced which can be laid (again without rotation) to form a 9x9 array with edges matching. This was proposed by Mrs A. Bricknell in IMA Bulletin November-December 1984 p>185 (Problem number 82). It was further required that a 4x4 pattern using only two of the colours be incorporated in the mosaic. The folowing solution was given in the next issue (but using different colour scheme and orientation). It will be seen that each lattice line, dividing the board into the 81 squares, has the same colour on either side along its length, Also the outer edges are all of one colour (white) so that the pattern can be circularly permuted (as if on a torus) and the 4x4 can then appear anywhere in the 9x9 array.

I have a note that I found the following solution on 27 January 1985. It was published in the Puzzle Column of the IMA Bulletin July-August 1895.

This pattern shows that two simultaneous 4x4 arrays of two colours can be incorporated into the 9x9 three-colour array. The patterns formed by the two darker colours (black and green) are complementary (i.e. one is the reflection of the other in a diagonal).
I found the above notes among my papers dating from 1985 and thought it was time they were put on this section of the website, July 2022. Only a delay of 37 years!
Readers may like to extend these patterns to larger squares.