The 108 pieces of 7 squares were first counted by F. Douglas and W. E. Lester in FCR April 1937.
A listing of the pieces was made by Frans Hansson in 1938, following a similar scheme to that used in FCR
for the pieces 1 to 6, however no 7-square piece dissections were published in FCR, so the numbering was not used.
A listing of the pieces by the binary number method is shown here
The first ever assembly of the 108 pieces of 7 squares. Done by Walter Stead on 5th June 1955,
but not published as far as I know until it appeared on the cover of Chessics #28, Winter 1986, p.137.
The pieces cover a square of side 28 units, leaving a central pattern of 28 uncovered squares.
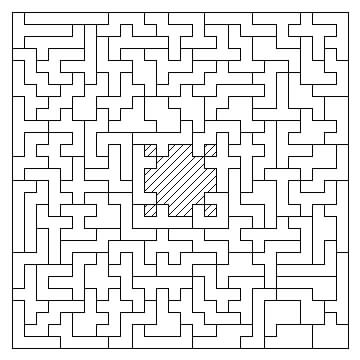
This diagram is included in three manuscript booklets of "Problems and Puzzles" by Walter Stead,
which in 1986 were in possession of his son Philip J. Stead. Walter Stead edited the
"Dissections" items in the Fairy Chess Review from February 1953 to February 1957.
From W. Stead's manuscripts. A solution by David Bird, dated 3rd June 1965 of the problem of arranging the 108 7-square pieces.
They form a "diamond" with 20 squares along each serrated edge (39 squares along the diameter)
leaving a central quincunx of uncovered squares.
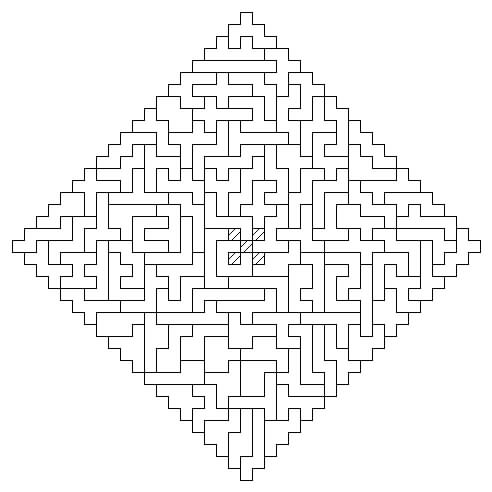
This was published on the back page of Chessics #28, Winter 1986, p.152.
A special issue on Chessboard Dissections. It may have been published somewhere else earlier.
Does anyone have biographical information about the composer?
In this construction, using all the 108 7-square pieces, with the piece with a hole in the centre,
Walter Stead has solved the problem of fitting the heptominoes into a 21×37 = 777-square rectangle,
with 21 gaps (5 at each corner and 1 in the centre).
In the notebooks it bears the date of 26th August 1973 and the title "The Square Spiral".
Mr Stead died 23 June 1976, aged 78, so this must have been one of his last, and finest, achievements.
This dissection (in a black and white diagram) was published in Chessics #28, Winter 1986, p.147.
The colouring scheme using six colours, with no two adjacent pieces having the same colour,
was devised by George Jelliss and used by him as a desk-top background on a personal computer,
and on an MSN Group relating to Mathematical Recreations (now defunct).

