The Centre of Similitude
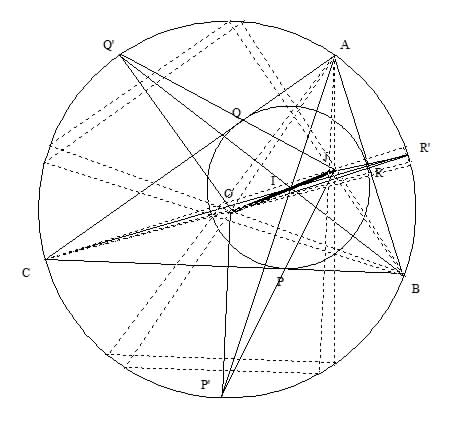
In this diagram we show the incircle and the circumcircle of triangle ABC. The angle bisectors which determine the incentre I, and the perpendicular bisectors of the sides which determine the circumcentre O, meet in pairs on the circumcircle at points P'Q'R' which bisect the arcs AB, BC, CA. The lines PP', QQ', RR' where P, Q, R are the points where the incircle meets the sides of the triangle, are concurrent at a point J which is the centre of similitude of the two circles.
All lines from J to the circumcircle are bisected by the incircle. The centres O, I, J are in a straight line, which is of course the axis of symmetry of the two circles, joining their centres. JO/JI = R/r the ratio of circumradius to inradius (Proof: R = OP', r = IP and triangles JOP' and JIP are similar).
In the example shown H is too close to J to show clearly. Is the isogonal of J on the incircle?