
The total of geometrically distinct closed 6×6 tours is 1245. These consist of 5 with quaternary symmetry, 17 with binary symmetry and 1223 asymmetric. Thus since an asymmetric tour can be presented in 8 different orientations, a binary symmetric tour in 4 different orientations and a quaternary symmetric tour in 2 different orientations there are 5×2 + 17×4 + 1223×8 = 10 + 68 + 9784 = 9862 possible distinct tour diagrams.
The 5 tours with quaternary symmetry were enumerated by Paul de Hijo (1882) and the 17 tours with binary symmetry were enumerated by Maurice Kraitchik (1927) though these authors may have been anticipated by Carl Adam (1867), a source I have not yet been able to examine. The number of distinct tour diagrams, 9862, was first correctly reported in a computer study by J. J. Duby, "Un algorithme graphique trouvant tous les circuits Hamiltoniene d'un graphe", Etude #8, IBM France, Paris 22/x/1964 [this information is from Prof. D. Singmaster]. Pre-computer era attempts at this enumeration had been reported by F. Fitting (1924, 1953) who cited a total of 10298 diagrams, and by H. J. R. Murray (1942) who arrived at a total of 1240 geometrically distinct tours.
There are just five closed knight tours with quaternary symmetry on the 6×6 board. They were given by Paul de Hijo (1882) [and possibly earlier by Carl Adam (1867) but I have not yet been able to check this reference] and these most attractive tours have been independently rediscovered many times since, e.g. by Bergholt (1918) and Cozens (1940). The central angles of the 5 quaternary tours are in our lettering a, e, g, i, l, all four angles in a quaternary tour being of the same type of course. The 'a' tour uses 12 slants (8 provided by the 'a's, and 4 others) but the 'e', 'g', 'i' and 'l' tours use only 4 slants (in these, each central angle provides one slant).

Probably the simplest method of finding all the tours of this type is the graphical one of using blank diagrams and drawing in all the possible patterns of angles on the four central cells, then step by step filling in all possible quaternary linkages between these given moves and the vacant cells. For example the impossible case of four f-angles is illustrated below. First put in the f-angles and the moves through the corners, which are common to all closed tours. Then the moves through the next-to-corner cells a5, b1, e6, f2 are fixed (since moves like a5-c4 are blocked). Then the moves through the edge cells a4, c1, d6, f3 are fixed (since moves like a4-c3 and a4-c5 are blocked). We now have two eight-move short circuits (a2-c3-b5-d6-f5-d4-e2-c1 is one), showing that a tour with these centre angles is impossible. We can however join up the loose ends (a3-c2 etc) to form a quaternary pseudotour of three component paths. The c-angles similarly produce a quaternary pseudotour of five circuits.

A method that may be considered more 'systematic' or mechanical is to use the octonary numbering of the board, and the list of permissible knight-move transitions. The procedure is to list all possible sequences of cell numbers, starting say from 0, seeking a sequence in which each diagonal number (0, 2, 5) occurs once and each off-diagonal number (1, 3, 4) twice. If one arrives at a sequence of less than nine numbers which cannot be extended because the numbers have already been used one deletes that sequence.
To shorten the procedure one can also take account in advance of other deducible features; such as that the transition 11 cannot occur in oblique quaternary symmetry (since by itself it forms a four-move circuit), and that if an off-diagonal number is repeated one of the numbers between the two occurrences must be a diagonal number (for example 343 represents a switchback, but 323 is two moves across the diagonal; and sequences like 3413, 1431, 4134 cannot occur since they prevent the corner moves 151 which must occur).
Beginning at the centre (0) one ends up with the ten sequences: 0151432340, 0234151340, 0234151430, 0323415140, 0341514320, 0415132340, 0415143230, 0431514320, 0432315140, 0432341510 (where the 0 has been repeated at the end to indicate closure). These occur in pairs that are reversals of each other. This duplication serves as a check on the correctness of the count. This type of method, with different numberings, was used by de Hijo (1882) and Bergholt (1918) in their solutions of this problem.
There are a further 17 closed knight tours with binary symmetry (necessarily rotational symmetry of Eulerian type) on the 6×6 board. Euler (1759) gave a single example. The complete set was first given by Kraitchik (1927) [or possibly much earlier by Carl Adam (1867)]. The central angles of the 17 binary tours are a/b, a/l, b/c, b/i, b/n, c/d, c/f, c/g (3 times), c/l, e/g, f/g, f/i, g/i, g/n, i/l, two angles being of one type and two of another. No case is possible in which all four angles are alike; tours with angles all alike turn out to be either quaternary or asymmetric. Using the graphical approach it is quite simple to check this enumeration of the tours that have binary symmetry. In terms of number of slants there are: 1 with 12 slants, 10 with 8 slants and 6 with 4 slants.

Diagrams of all 1223 tours of this type are shown on the following catalogue pages.
Asymmetric tours with 4 or 12 slants: Total 60 + 44 = 104.
Asymmetric tours with 6 or 10 slants: Total 304 + 288 = 592.
Asymmetric tours with 8 slants: Total 527.
To enumerate symmetric tours a symmetric numbering of the cells of the board provides an effective method (used by de Hijo 1882). My preference is for a system of numbering that is applicable to any square board, in which the n(n+1)/2 distinctly placed cells on a square board of side 2n or 2n – 1 are coded from 0 in the centre to (n^2 + n – 2)/2 in the corners; the other cells being numbered systematically from the centre outwards rank by rank. [See diagram below and in Part 1.]
Within the 6×6 frame by omitting the centre cells the border can be filled in one way by four 8-move equal circuits. This suggests one way of enumerating all possible closed tours on the 6×6 board in a manner analogous to that used for the 5×5 board. Moves in a tour are either round the four circuits (moves with codes 51, 14, 43, 32, 23, 34, 41, 15), or from one circuit to another (codes 11, 13, 31), or into and out of the centre cells (01, 02, 03, 04, 10, 20, 30, 40). This seems to have been the method employed by Fitting.
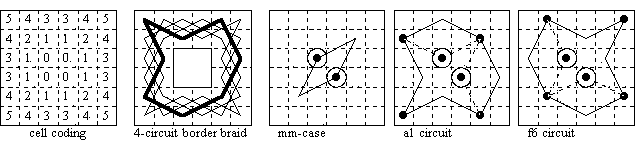
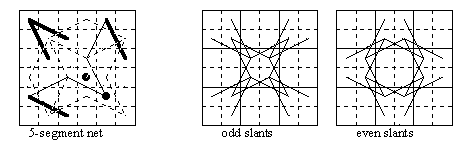
The central 2×2 is just one of 9 blocks, each 2×2, into which the 6×6 board is divided by grid lines drawn between every second rank and file. A knight placed anywhere on the board always moves from the block in which it stands to a neighbouring block, that is either to one with a side or one with a corner in common with the initial block. Knight's moves of these two types were usefully termed by H. J. R. Murray straights and slants respectively. An alternative way of defining them is that a knight move is a straight if it crosses one grid line, and a slant if it crosses two grid lines.

The straight knight moves on the 6×6 board form four separate nets of moves, each topologically equivalent to the moves of a wazir on a board 3×3. Thus wazir paths on the 3×3 board (called the block diagram by Murray) correspond to knight paths of straights on the 6×6 board. It is because the straights form these tourable nets, and the wazir paths are easily counted, that this method is a useful one for classifying and enumerating tours. If we letter the four nets L, E, A, P we arrive at the indexing system shown. This method of analysis was first developed for the 8×8 board by P. M. Roget (1840) and extended to even boards in general by Murray (1942).
The straights are moves LL, EE, AA, PP indicated by two letters the same, and slants are moves LA, LE, PA, PE (or vice versa) indicated by two different letters, one a consonant and the other a vowel. The straights move the knight within a net, while the slants move it from one net to another. Moves of types LP and EA (or vice versa) connecting consonants or vowels are always impossible.
On the 6×6 board the four nets are of the same shape, and each net passes through one corner of the board. It will be seen that the nets are made up of squares and diamonds linked together. If we number the cells of the smaller 3×3 board, or block diagram, then the cells of the larger board are uniquely determined when we specify the number of the block and the letter of the net. Thus the top left corner is L1 in this scheme. I call this method of labelling the cells the intrinsic coordinate system.
Further, if we make the numbering in accordance with a wazir tour, say boustrophedonally as shown above, then the blocks are numbered odd and even, in a chequerboard fashion. We can then classify the slants as odd slants or even slants according as they connect odd or even numbered blocks. On the 6×6 board the odd slants all have one end in the central block, so the two types could be called radial slants and orbital slants (this terminology however is not appropriate on larger boards). Straights always connect odd to even blocks.
The number of slants in a tour provides a way of classifying tours according to their complexity of structure. The number of slants in a tour must be at least 3, since each change from one net to another (e.g. L to E) is made by a slant move, and there are four nets to be visited. In a closed tour the number of slants must be even, since the last slant must return to the initial net. Combining both these results the least number of slants in a closed tour is 4.
The total number of slants on the 6×6 board is 32, since there are 2 vertical grid lines on each of which there are 4 strands of 2 slants, and 2 horizontal grid lines on each of which there are also 4 strands of 2 slants. The maximum number of slants that can occur in a closed tour is 4 less than half the number of slants, that is 12 on the 6×6 board.
In a closed tour each net is divided into a number of segments, made up of one or more straights or consisting of a single cell. If l, e, a, p denote the numbers of segments into which the L, E, A, P nets are divided in a given closed tour then l + e + a + p = S, the number of slants, since the tour consists of a sequence of alternate segments and slants.
The number of slants incident with a net is twice the number of segments into which it is divided (or equivalently the number of segments is half the number of incident slants), since each segment has one slant at each end. Each slant has one end in a consonantal net and the other end in a vowel net, since there are no LP or EA connections. Thus the number of slants incident with the consonantal nets is S, and the number incident with the vowel nets is S, since each slant is counted twice, once from each end. It follows that l + p = e + a = S/2. This implies the previous equation but is a stronger condition.
This result provides a way of subclassifying the tours according to the way the segments are shared between the nets. For example, when S = 8 we have l + p = e + a = 4 and if net L is toured in 1 piece then net P must be toured in 3 pieces, while if L is in 2 segments, P must be in 2 segments. Tours with 8 slants are thus of three types according to the minimum number of segments in the consonant and vowel nets: (1,1), (1,2), (2,2). In the minimal case of 4 slants each net is toured as a single piece, so only the (1,1) case occurs.
On the 6×6 board a division of a net into 5 pieces is possible, but does not lead to any tour. For example the L-net can be split into the segments b4-a6-c5, e6-f4, a2-c1, d3, e2 including two isolated cells, but the slants incident at e2, a2, e6 meet at c3, d4, thus eliminating any slants incident with b1, b5, f5 in the P-net, forcing the f1-circuit. Thus the partitions possible are: 4 (1:1), 6 (1:2), 8 (1:3) (2:2), 10 (1:4) (2:3), 12 (2:4) (3:3).
Reflection of the board in the principal diagonal interchanges the A and E nets. Reflection in the secondary diagonal interchanges the L and P nets. Rotation 180° combines both these effects. Reflection in the vertical median interchanges L with E and P with A. Reflection in the horizontal median interchanges L with A and P with E. Rotation 90° clockwise causes the cyclic changes L - E - P - A - L. Rotation 90° anticlockwise causes the reverse cyclic changes L - A - P - E - L. By these rotations and reflections we can always orient an open directed tour so that the first slant is of LE type.
In any net on the 6×6 board there are 5 odd cells (i.e. in the odd-numbered blocks) and 4 even cells. A net traversed in one path thus begins and ends on odd cells, from which it is linked to the other nets by odd slants (a diagram of the even slants appeared in Fitting 1953). Other breaks in the net introduce one odd and one even cell and corresponding slant. Thus in a closed tour the number of odd slants is always 4 more than the number of even slants. In tours with 4, 6, 8, 10, 12 slants the even:odd distribution is 0:4, 1:5, 2:6, 3:7, 4:8 respectively. Since the odd slants are all incident with the centre cells, the numbers of pairs of slants meeting at centre cells is respectively 0, 1, 2, 3, 4.
Since there are four cells forming a 2×2 square at the centre of a 6×6 (and any even-sided) board, a method of classifying tours on these boards is by the pattern formed by the four angles on the central squares. These angles can be specified by the numerical coding of the three cells used (numbered from the centre outwards as shown) but it is briefer simply to letter the angles.
In Chessics 1985 I used the following lettering of the angles: 404 = a, 403 = b, 402 = c, 401 = d, 401 = e, 402 = f, 403 = g, 303 = h, 302 = i, 301 = j, 301 = k, 302 = l, 202 = m, 201 = n, 201 = o, 101 = p (where an underline indicates the move does not cross the diagonal). In closed tours, case 'p' cannot occur on the 6×6 board since it forms a 4-move circuit with the moves through a corner cell.

In Chessics 1987 I reported on how the central angle method could be used to enumerate all the asymmetric closed tours. The first stage in the enumeration is to consider all ways the knight can pass through a pair of diametrally opposite centre cells (e.g. c4, d3). The 15 angles (a to o) form (15×16)/2 = 120 pairs. If one of the angles is symmetrical about the diagonal through the two central cells (i.e. type a, h or m) then the pair can occur only in one geometrically distinct form, but if neither is symmetric then the pair occurs in two geometrical forms. The number of asymmetric angles is 12, so the number of pairs of these angles is (12×13)/2 = 78. Adding these two figures, 120 + 78 = 198, gives the total number of geometrically distinct pairs of angles to be considered. Many of the 198 pairs can easily be shown to be impossible of occurrence in a closed tour.
The case mm eliminates itself by forming a four-move circuit in the middle of the board. If no moves from the centre angles c4, d3 go to the three cells a5, e5, e1 then an eight-move circuit (one of the strands of the border braid) is forced through these cells and the corner a1. Similarly for the three cells b2, b6, f2 and the corner f6. The angles a, f and m (formed of 2 slants) disrupt both these circuits and so can potentially form tours in combination with any other angle. The angles h, j and k (formed of 2 straights) disrupt neither circuit and so cannot form tours unless in combination with angles a, f or m. The other angles disrupt only one of the circuits (c with 2 slants disrupts the same circuit in two places). Pairs of cases occur with angle f since it is asymmetric; the other two angles that disrupt both circuits, angles a and m, are symmetric.
By these arguments we eliminate 100 cases and are left with 98 to consider: aa, ab, ac, ad, ae, af, ag, ah, ai, aj, ak, al, am, an, ao, bb, bc, bd, be, 2bf, bg, bi, bl, bm, bn, bo, cc, cd, ce, 2cf, cg, ci, cl, cm, cn, co, dd, de, 2df, dg, di, dl, dm, dn, do, ee, 2ef, eg, ei, el, em, en, eo, 2ff, 2fg, fh, 2fi, 2fj, 2fk, 2fl, fm, 2fn, 2fo, gg, gi, gl, gm, gn, go, hm, ii, il, im, in, io, jm, km, ll, lm, ln, lo, mn, mo, nn, no, oo.
Each closed tour contains four central angles and shows two of the 98 cases listed. We can indicate the type of tour by a code of the form uv/wx where uv is one pair of diametrally opposite centre angles and the other pair is wx. The 5 doubly symmetric tours are of type uu/uu (reduced to 'u') and the 17 singly symmetric tours are of the form uu/vv (reduced to 'u/v'). In enumerating the tours, we work through systematically from a to o.
During October 1992 I applied this angle method to enumerate all the asymmetric tours, but it proved necessary to cross-check the results by the slant method to ensure accuracy. The enumeration procedure made use of sheets of blank diagrams, first enumerating all tours with 'a' on c4 and successively 'a', 'b', ..., 'o' on d3, then all tours with 'b' on c4, but no 'a's anywhere, then all tours with 'c' on c4, but no 'a's or 'b's anywhere, and so on in alphabetical order. To reduce the labour I followed the procedure of first eliminating any symmetry, so that duplicates due to rotation or reflection are not generated. In December 1992 Prof. D. E. Knuth sent me a complete print-out enumerating the tours, in a numerically coded form, produced by a computer method based on slants.
Pairs of slants meeting at the centre cells form the angles a, c, f, m, while pairs of straights form the angles h, j, k, p. Other angles use one slant and one straight. In the catalogue I list the tours first according to their symmetry (quaternary, binary or asymmetric) then their number of slants (4, 6, 8, 10, 12) and then according to their central angle codes, in the partial alphabetical order: a, c, f, m // b, d, e, g, i, l, n, o // h, j, k, p.