There is a long tradition of chess, magic squares and knight's tours in the Indian subcontinent, including Kashmir and Sri Lanka (Ceylon). This page is a survey of work from Indian sources, and may duplicate work in other sections. In particular we include here diagrams of all the tours attributed to the Rajah of Mysore, as given in Indian Chess by S. R. Iyer (1982) and based on Harikrishna (1871).
(c. 900) Rudrata Kavyalankara Kashmir in the reign of Sankaravarman 884-903. [Commentary by Nami of Guzerat 1069. Analysis by H. Jacobi 1896, and Murray 1913, pp.53–55].
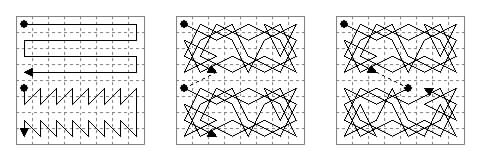
This is a verse work which includes a simple boustrophedonal tour by rat-ha (chariot, i.e. rook) and a sawtooth tour by gaja (elephant) as well as a tour by turaga (horse, i.e. knight), all on the 4×8 half chessboard. These tours were presented by a series of syllables on the squares which make sense when read in the sequence of the tour (i.e. what I call a cryptotour). Murray maintains that the verse also makes sense when read normally; this may be true for the simpler tours, but seems very improbable to me in the case of the knight's tour.

The elephant, which is a piece still in use in Burmese and Thai forms of chess and was described by al-Beruni as used in India, is a {1,1}-mover (i.e. one step diagonally) with the extra power of a single pawn-like forward step (the five moves thus representing the elephant's four legs and trunk). I have shown the form of tour proposed by Murray, rather than that given in the commentary which, when numbered 1-32 has 17 at the start of the third row down so that 16-17 is not an elephant move. This also ensures that, like the rook tour, the columns are magic (all add to 66), being formed of pairs of complements adding to 33.
Rudrata's knight tour can be repeated on the lower half of the board so as to give a complete though not closed tour. A diagram showing it in this form, reflected left to right, appears in 'a Persian manuscript of the early 19th century probably compiled in Northern India', described by Walker (1844). Another version, in which the half-board tour is rotated 180° on the lower board and slightly modified to join to the upper half appears in the Manasollasa of Somesvara III (c. 1150), described by Bernhauer (1997).
(1069) Nami of Guzerat. Commentary on Rudrata (c. 900) Kavyalankara.
(c. 1150) Somesvara III. The Manasollasa {translated 'Freude des Geistes' i.e. 'Delight of the Spirit' a traditional sobriquet for chess} is described by Bernhauer (1997) as a 'Fürstenspiegel' ('Princely Mirror') written for King Somesvara III of the Kalyani area in central India (c.1150).
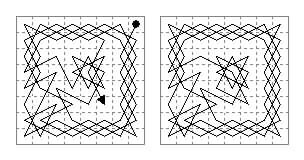
The tour in this source is of the edge-hugging type, a form typical of many later constructed [e.g. Mani 1350, and De Moivre 1722] beginning at a corner, skirting the edges and ending in the central 4×4 area. The tour is described in the form of a list of two-letter coordinates. Bernhauer gives the open tour shown in the first diagram below.
However, the sequence of syllables is somewhat corrupt and, as listed on the third page of Bernhauer's article, ends with the cell a knight's move from the corner. This suggested to me that the tour was intended to be closed, and led me to the second diagram which seems the most likely interpretation in my view.
(1640) Bhatta Nilakant-ha Bhagavantabhaskara {Sun of Bhagavantadeva} in 12 Rays {Mayukhas}. Has a section on chess at the end of the fifth book. Gives one tour, presented in three different ways, numbered from different points, the first two cases being attributed to Nilakant-ha's ancestors. [The tour is also given in Monneron (1776), Shir Muhammad-Khan (1796), Harikrishna (1871), Weber (1873), Stenzler (1874), Hoffmann (1893), Murray (1930) and S. R. Iyer (1982)]

The Bhagavantabhaskara is a Sanskrit work on ritual, law and politics. According to Maurice Winternitz History of Indian Literature p.607 (extract in Google Books) it was written at the command of the Rajput prince Bhagavantadeva in about 1640. If the tour was in fact composed at this date it is a very remarkable isolated achievement, being a fully symmetric closed tour, before the work of Euler (1759), but possibly it may be a later addition. This tour first became known outside India in an article by Monneron (1776).
(1776) — Monneron. Writing from the East Indies, supplied two tours to the Nouveau Dictionaire, Pancoucke, Paris. The first of these is the Nilakant-ha tour (see c.1640). The second tour is ascribed to a Malabarese (from Malabar in south-west India). Both tours are quoted in Hoffmann (1893) who gives this tour the heading 'Du Malabar' as if that was the name of its author. This Dictionaire may be the source of the statement, quoted by Lucas (1882) and Kraitchik (1927), that knight's tours were known in ancient times in India.

(1798) Shir Muhammad-Khan. Sardarnama manuscript. Described by Murray as Persian, but written in central India. Contains the Nilakant-ha tour. [Murray, 1913, p.65 footnote and p.181]
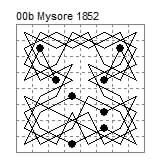
(1852) Krishnaraj Wodayer, Rajah of Mysore. A rectangle of silk, dated 31 July 1852, bearing a magic 8×8 knight's tour.
The 8×8 tour on the silk was independently discovered by Francony in 1881, and appeared in N. Rangiah Naidu's Feats of Chess 1922 without mention of its author.
Murray (1951) wrote: 'It was not known in Europe until 1938 that Indian players had also busied themselves with magic tours and that a closed unsymmetrical magic tour had been discovered in Mysore on 31 July 1852. A contemporary silk handkerchief bearing this tour, which it ascribed to Maharajah Kristna Rajah Wodayer Bahaudah, the Rajah of Mysore, was exhibited at the Margate Easter Chess Congress, 1938.'
Another sighting of this silk was reported by Major J. Akenhead (1947) in a letter dated 12 March 1947 to Fairy Chess Review, vol. 6, April 1947, p.84: 'I was in Mr A. Hammond's (Emil, Burlington Gardens) yesterday and found that he had a piece of silk framed on which was a magic knight-tour invented, as the wording stated by Maha Rajah Kristna Rajah Wodaye, Behauder Rajah of Mysore, on 31st July 1852.'
Currently the silk is in the chess collection of Jon Crumiller of Princeton, New Jersey, USA. It was on display at the World Chess Hall of Fame in St Louis in 2013.
It is a closed tour of squares and diamonds type and is fourfold magic in that it can be numbered magically from four different origins by cyclic shift of the numbering (i..e from f5, d1, b7 as well as f3). The diagram on the silk and in Iyer (1982) is numbered from f3 to d4.
Some background history may be of interest here. Mysore in central India was annexed by the British following the death of Tippoo at Seringapatam 1799. What happened next is told in The Golden Book of India by Sir Roper Lethbridge, 1893, pp.362-8; in summary: 'The British resolved that Mysore revert to control of the family of its ancient rulers. An infant son of Chamraj, by name Krishnaraj, was placed on the throne. During the minority of the Maharaja Krishnaraj 1799–1810 the state was administered by a Diwan or Prime Minister, the famous Purnaiya. The affairs of the state however fell into disorder after the retirement of Purnaiya; and the 'misgovernment' of the Maharaja was terminated by the British Government assuming the direct administration in 1831, retaining the Maharaja as titular sovereign. On the 18th June 1865 the Maharaja adopted as his son and successor the young prince Maharaja Chama Rajendra Wadiar, whose adoption was sanctioned in 1867. Maharaja Krishnaraj died in 1868. The rulers of Mysore were called Wadiar or Wodeyar, being a plural or honorific form of Odeya, Kanarese for Lord.' Assuming the age of majority in India was 21 would give the date of birth of Krishnaraj as 1790.
(1868) Krishnaraj Wodayer, Rajah of Mysore.
Many other tours attributed to the Rajah of Mysore, Krishnaraj Wodayer (1790-1868) were included in the manuscript of an encyclopedia compiled in 1871 after his death. For details of this see Harikrishna (1871). This work was printed in India in 1900. The tours in the manuscript were included in the work Indian Chess by S. R Iyer (1982) which is an edited version of the chess section of this Sanskrit work, with notes in English. A copy of this 1982 work was obtained by David Pritchard for the BCVS, and further details given here are from this book.
The 8×8 magic tour is #37 among the 82 tour diagrams given in this work. Of even greater interest than the 8×8 magic tour is the inclusion of a 12×12 magic knight's tour, diagram #3, also formed on the squares and diamonds principle. It is numbered from g2. This is the earliest known magic knight's tour on a board larger than the 8×8.
The existence of this tour was not known to Murray. No other magic tour on a larger board is known until 1885, when Wihnyk gave a 16×16 example, and no other on the 12×12 is known before 1932 when E. Lange added a border to an 8×8 tour.

The snake-like pattern of this tour is similar to that of tour (11) by von Schinnern (1826), and one wonders if von Schinnern's little book was in the Rajah's library.
The magic tours are certainly the highlights of the collection of tours attributed to the Rajah. The quality of the tours vary, from these highly structured magic tours to trivial-seeming pictorial tours in which the knight moves just fill in the shape rather arbitrarily. One may wonder whether the Rajah did all this work himself, or engaged servants or even children to do some of it, but it appears he had plenty of leisure time to devote to such pastimes since, as noted above, he was relieved from power by the British in 1831.
The text relating to knight's tours in Indian Chess is section 9 (pp.29-47) together with 82 diagrams in an appendix of 61 pages. Tours 1-76 are said to have been 'mentioned by the King of Karnataka, H. H. Shri Krishna Udayar.' Karnataka is the modern name (since 1973) for Mysore, so the King of Karnataka may be identified with the Rajah of Mysore.
We now give diagrams of all the other tours in the collection, grouped according to type. The first 34 tours are on the 12×12 board, and the rest on the 8×8.
Magic and Figured Tours with Numerical Properties
#1 has the numbers 2, 8, 16, 24, 32, 64, 72, 144 in a circle round the initial cell. These apart from 2 are multiples of 8, but the other 11 multiples do not form any particular pattern. The text says that the nine marked cells add to 363 but the significance of this number is not explained.
#3 is the 12×12 magic tour shown separately above.
#4 is magic in the files (sum 870) but the rank sums take ten values from 776 to 966.
#5 is magic in the ranks and each 4×4 block adds to 1160, the first four files also add to 870, but the others add to 872 or 868.
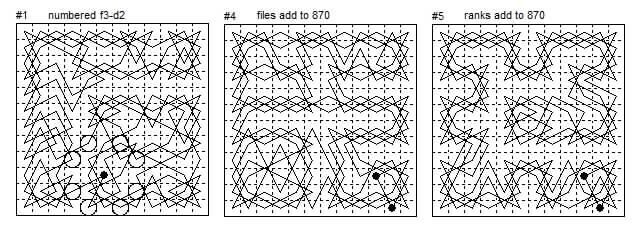
#6 adds to 870 along the main diagonals, the numbers on the diagonals being: 19, 43, 67, 69, 85, 87, 137, 73, 53, 79, 129, 29 and 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 100, 110. The rest of the tour seems somewhat random.
#10 has the numbers 2, 18, 36, 54, 72, 90, 108, 144 in a circle round the initial cell. These apart from 2 are all multiples of 18 (the 7th multiple 126 is at b9).
#34 has the ranks and files of the centre 4×4 all adding to 354. The 2×2s surrounding it all add to 282, as do other 2×2s in the surround.

#35 has the numbers 2, 8, 16, 24, 32, 40, 48, 64 at a knight move from the intial cell f4. Apart from 2 these are multiples of 8, the missing multiple 56 is at c7.
#37 is the 8×8 magic tour shown at the start of this article.
#38 and #39 are squares and diamonds tours the first magic in the ranks and the second with magic files.
#40 has diagonals adding to 260, the numbers in the diagonals being 23, 27, 29, 15, 37, 35, 55, 39 and 8, 20, 16, 10, 52, 46, 58, 50.
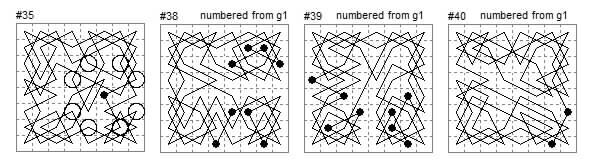
#61 has 10 and its multiples 20, 30, 40 50, 60 a knight move from the initial cell.
#62 has 5 and its multiples 10, 15, 20, 25, 30, 35, 40 on the middle cells of the main diagonals - the other multiples of 5 are at f8, g6, f2, h3).
#63 has an AP of difference 3 (1 - 22) along the third rank and an AP of difference 5 (26 - 61) along the fifth rank. This is also an open compartmental tour, 3×8 joined to 5×8.
#65 also has an AP of difference 3 (3 - 24) along the third rank, and is a closed compartmental tour, 3×8 joined to 5×8.

#67 has 8 and its multiples in sequence along the a1-h8 diagonal.
#74 has the four outer ranks and files all adding to 244, as do the rectangles ab36, gh36, cf12, cf78. The four inner ranks and files all add to 276. The four numbers in each corner add to 122. Each row and column in the central 4×4 adds to 154.
#75 has each row and column in the central 4×4 adding to 150, and the four numbers in each corner adding to 120.
#76 has each row and column in the central 4×4 adding to 154. The four numbers in each of the surrounding 2×2 grid areas all add to 122.

Patterned Tours
#7 is composed of 3×9 and 3×12 sections.
#8 has the Euler cross tour in the centre.
#9 is a bordered 6×6 tour.

#11 is very unusual in that the moves 1-43 and the moves 144-102 form the same pattern but shifted by a knight move. The other moves 43-102 just fill in the gaps.
#18 is a 'two-horse movement' each tour of 72 cells. When numbered the pairs of same numbers occur in adjacent cells, forming a division of the board into dominoes; one pair of dominoes being vertical, the others all horizontal. This could easily be converted into a tour, e.g. by replacing g10-h12 by g10-i11 and i10-h12.

#41 has the moves 1-16 and 17-32 each occupying two cells in every rank and every file (i.e. a bisatin) but the same is not true for 33-48 and 49-64.
#42 shows two matching 12-move sequences.
#43 has star-patterns at the corners called 'ponds'.
#66 has the Euler cross at the centre.

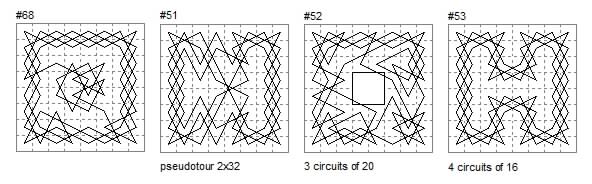
#68 has 15-move 4×4 tour at centre.
#51 is an axially symmetric pseudotour of two 32-move circuits.
#52 is a pseudotour of three circuits of 20 moves (omitting the centre 2×2).
#53 is a pseudotour of four paths each of 16 moves: the H-crosspatch pattern.
Tours of Octonary or Biaxial Shaped Boards with Holes
In the original diagrams as shown in Indian Chess these tours are shown on 12×12 boards with some cells not used, or marked by dots. I prefer to show the unused cells as cut away, certainly round the edges.
#2 omits the diagonals and cells next to the corners, resulting in a loosely connected board.
#12 omits the centre 4×4 and the corner 2×2s. In the original it is shown on the 12×12 board with Indian script in the unused cells.
#13 is said to represent the ramparts of a fortress. The lines delineating the areas do not appear on the original diagram. Here some board sections are completely disconnected.

#14 has five cross-shaped areas that are said to represent ponds with connecting steps leading to them. This board is loosely connected.
#15 is said to represent a lake with a platform in the centre. In this case the board shape is delineated on the 12×12 diagram.
#16 covers 112 cells. The corners and central region are loosely connected.

#17 has nine areas omitted which are said to represent ponds.
#19 is (like #18) a 'two-horse movement' formed of two open paths. Again just two dominoes are vertical; 30 at h67 and 32 at e67. This can be converted to a tour by the linkage: h9-f8-e6-g5-h7-g9.
#23 (100 cells) is said to represent two intertwined serpents. Pictorial tours of this type have line drawings on the diagrams, depicting various objects or animals.

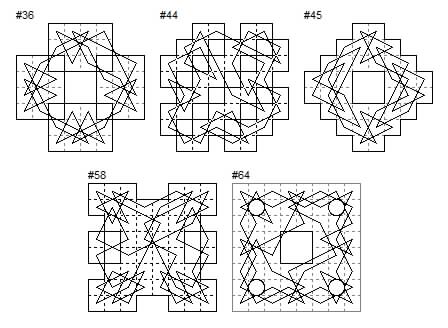
There are five 8×8 examples of this type. #36 (40 cells, board of four loosely connected components) tour has a diagonal axis of symmetry. #44 (40 cells, board of four loosely connected components, biaxial diagonal axes) described as leaving one space blank in front of each move. #45 tour of a 36-cell board with central hole. #58 (52 cells, two loose sections biaxial, lateral axes) depicts two intertwined serpents. #64 tour of 56 cells, 8 cells omitted forming five holes.
Pictorial Tours
There are two connected examples with axial symmetry. #20 (86 cells) depicts an aerial chariot, and #25 (74 cells) a tree.

#21 (108 cells) depicts 'an installed Shiva-linga'. There is a hole at k6 where the handle occurs. #22 (102 cells) depicts a seated bull. There is a hole at e9 between ears and hump. #27 depicts an elephant, with a hole at k11 where the trunk curls round.

#28 (74 cells) depicts a prancing horse, with holes at b6 and j3 between front and rear legs. #29 (92 cells) depicts a swan (looks more like a duck to me). Holes at c6, d2, f2. #30 (98 cells) depicts a peacock. Single holes at b10 and f2, and two two-cell holes.

In some of the pictorial tours the cells used form boards that are only loosely connected. #24 (86 cells) depicts a serpent, coiled around the hole at g3, with tail at a8 and tongue on the loosely connected cell at b10. #26 (102 cells) depicts a cow and calf, with loosely connected tail. The head is a 3×4 tour. #33 depicting 'baby Krishna tied to a mortar' is of the asymmetric but connected type.

There are six tours on the 8×8 board of this type. #54 (40 cells, one hole) an installed Shiva-Linga. #55 (40 cells, one hole) Bull. #56 depicts an elephant (42 cellls, two loose sections). #57 (38 cells) Horse. #59 (44 cells, one loose) represents a serpent. #60 (42 cells, axial symmetry) shows a vase.

Tours with other moves besides the knight.
Tours #31, 32, 46, 47, 48, 49, 50, 69, 70, 71, 72, 73 are of this type. To show the tours with reasonable clarity in graphic form it is necessary to curve the rook and bishop moves that are longer than one step. In the forms of Indian chess played by the Rajah the bishop-moving pieces are named 'camel' or 'flag-car' and the rook-moving pieces are 'elephant' or 'chariot'. There is also a 'minister' which moves like a king.
Tours #46, 47, 48, 49, 50 are alternating moves of knight and another piece, in the tradition of As-Suli (940). The other tours are increasingly elaborate attempts to include more and more pieces in the series. Tours #69, 71, 72 are on 60-cell boards, omitting four cells in centre or corners.
#46 is a knight - wazir tour.
#47 is a knight - fers tour.
#48 is a knight - bishop tour.
#49 is a knight - rook tour.
#50 is a knight - king tour (in this all the files add to 252, except the third which gives 316).
#69 is a knight - rook - wazir series.
#70 is a knight - rook - fers - wazir series tour.
#71 is a 5-piece knight - fers - rook - bishop - wazir series.
#72 is a 6-piece knight - fers - rook - bishop - king - wazir series.
#73 shows a series of series all on one board, 4 cells covered by knight, 6 by knight and rook, 9 adding king to the series, 12 adding fers, 15 adding bishop, 18 adding wazir.

Tours #31 and #32 on the 12×12 board are more ambitious forms of #72 and #73, showing up to an eight-piece series. In the diagram for #32 the numbers at c9 and d12 should be 25 and 23 (not 15 and 22). The eight series are of lengths 4, 8, 12, 16, 20, 24, 28, 32.

Tours 77-79 in the collection are the three versions of the one tour from Nilakant-ha's work (see 1640). Tours 80-82 are Harikrishna's own (see Harikrishna 1871).
(1871) Pandit Harikrishna Sharma Jyotishacharya Kridakausalyam. The tours constructed by Maharaha Krishnaraj Wodayer (see 1852) were preserved in this manuscript work. The following notes appear in Indian Chess by S. R. Iyer (1982) which is an edited version of the chess section of this Sanskrit work, with notes in English. 'The author of the present work is one Harikrishna, son of Venkataraman, who lived in Aurangabad in the Maharastra State. He wrote it in Saka 1793 (1871). These particulars are mentioned by the author himself in the last 5 verses of Kridakausalyam, which contains 700 verses in all. Harikrishna compiled a voluminous (encyclopedic) work [title in Indian script] which consists of six parts called Skandhas. Each part consists of several chapters, Kridakausalyam being the 20th chapter in the 6th part of that work. This chapter treats in 12 main sections of many indoor and outdoor games prevalent in his part of the country. The extract printed here [on chess and knight's tours] forms the 8th section. This book was printed in Devanagari script by Venkateshwar Steam Press, Bombay, in Saka 1822 (1900). Being long out of print, it has been reprinted with the financial assistance from the Sanskrit Division, Ministry of Education and Culture, Govt. of India, by Nag Publishers, Delhi, 1982, on the occasion of the 9th Asian games, Delhi-1982.' The text relating to knight's tours is section 9 (pp.29-47) with 82 diagrams in an appendix of 61 pages. For details see Krishnaraj Wodayer (1852). Tours 77-79 in the collection are the three versions of the one tour from Nilakant-ha (1640). Tours 80-82 are Harikrishna's own.
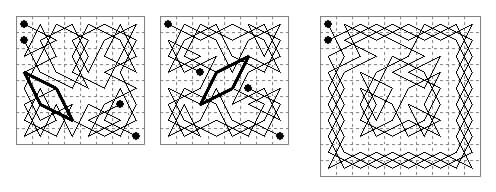
#80 and #81 are 'two-horse movements' on the 8×8 board. In each case the horses start in the corners and on cell 6 encounter the diamond path where they have two choices of cell 7, leading to two separate end-points. I suspect this is due to the words that are written along the path being readable in either way (but they are written in Indian script without translation). #82 is a conventional tour on the 10×10 board, similar to Ciccolini (1836).
(1884) Ambikadatta Vyasa. Chaturanga Chaturi. Twelve tours: (1) Euler's first open tour modified as a1 to h1. (2) Symmetric tour joining two half-board tours, similar to Euler. (3) Euler's 12-cell cross tour repeated four times in 8×8 board and joined up to make an open tour, omitting 16 cells in a pattern often seen on Indian boards. (4) Closed tour 7×8 in 3×8 and 4×8 compartments. (5) Open tour omitting 20 cells of 8×8, central 2×2 and 2×2 at middle of each edge. (6–7) Open and closed tours 5×8. (8) Symmetric tour 6×8 in two 3×8 compartments. (9-10) Near-symmetric open tours 4×8 and 3×8. (11–12) Open tours 6×6, one omitting four cells, b25e25. [Murray 1930]
(1885) — Syamakisora. Risala i Shatranj. Tour both Rhombic and Rogetian. [Murray 1930]
(1893) Vinayaka Rajarama Tope. Buddhibalakrida, (Marathi). Ten tours. Six open tours 4×8 and four 8×8 tours: (1) Euler type open tour identical to Vyasa (1884) but rotated a half-turn. (2–3) Tomlinson/Roget tour, closed, and slightly modified version of same. (4) Closed tour formed of two of the six half-board tours linked asymmetrically. [Murray 1930]
(1901) Lala Raja Babu (Sahib) Mo'allim ul Shatranj. 27 tours. (1–10) The first one is de Moivre's tour with the middle three moves reflected. The next nine are similar, the eighth incorporating a central 3×4 tour, the last two closed. (11) Euler's first symmetric bipartite tour. (12-17) Three open and three closed tours omitting various squares. (18–21) Four tours with approximate symmetry. (22–26) Open tours 7×8, 6×8, 5×8, 4×8, 3×8. (27) Open 10×10 tour joining four 5×5 tours. [Murray 1930]
(1922) Sammete Rangiah Naidu. Feats in Chess, published in India. Ch 2, with two plates, contains 100 diagrams of tours on the 8×8 or portions thereof, also the 12×12 and a T-shape of 80 cells. [Murray 1930 and 1955 §126]
(1923) R. C. Temple; Indian Antiquary 1923.
(1923) L. R. Ramachandra Iyer; Indian Antiquary 1923.
(2003) Awani Kumar.
In March 2003 Awani Kumar (India) solved the long-standing problem of a diagonally magic tour on the 12×12 board, obtaining four examples. These were also published online in The Games and Puzzles Journal, Issue 26.