Sections on this page: Introduction — X & N Notation — Contraparallel Chains — Contiguous Contraparallel Chains — Regular Magic Tours — Regular Tour Matrices — Murray's Testing Procedure — Irregular Magic Tours — Semi-Magic Tours
This treatment of tours on the standard 8 by 8 chessboard is based closely on the work of H.J.R.Murray (1936, 1942, 1951); principally chapters X–XII of his 1942 text and chapters I and III–VI of his 1951 version. The terminology however has been simplified, particularly relating to ‘quartes’. Because of the advent of computers many details of his procedures are now of mainly historical interest and are summarised. Passages quoted directly from Murray are within quote marks "...". Short inserted passages by the editor are within square brackets [...]. There are separate pages on the historical development, on the more general theory, and on the results achieved on particular boards.
In place of Murray's numbering of the 8 by 8 tours the system (00b, 12d, 27a, etc) introduced in my 1986 Chessics catalogue of the tours is used. There are 15 closed tours coded 00 (these are the cyclic tours that are magic when numbered from two or more different initial cells) which generate 47 reentrant tours. In the other cases the two numbers of the code are the coordinates of the move separating the end-points (1 and 64) of the tour. There are 9 tours coded 01, 7 tours 03, 7 tours 05, 1 tour 07, 16 tours 12 (these are the noncyclic reentrant tours), 6 tours 14, 1 tour 16, 17 tours 23, 2 tours 25, 20 tours 27, 7 tours 34. [Figures updated August 2003]
"Any knight's tour on the chessboard may be regarded as composed of 16 4-cell chains, and every number of move can be expressed in the form 4.x + n, where x may have any integral value from 0 to 15, and n is one or other of the four numbers 1, 2, 3 and 4. In other words x gives the number of chains which the knight has already completed, and n gives the position of the knight on the current chain."
These 4-cell chains we call quartes. A diagram showing only the quartes in a tour or potential tour we call a matrix. To construct a tour with a given matrix is to determine whether the ends of the quartes can be linked to make a complete tour; and to determine if it is magic.
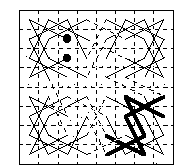
The following diagram shows the matrix for tour 01a with the links, shown by broken lines. The quartes shown by heavy lines are those of beverley type (see the Regular Tours section below).

In a magic tour we require 4.X + N = 260 in each line; thus a unit change in X necessitates a change of 4 in N, in the opposite direction, to preserve the magic total. Murray's explanation for the narrowed limits, "since 4 always links with 1", is incomplete. For example in the following symmetric tour of squares and diamonds type that I have constructed, the N-values add to 28 on the second and seventh ranks and 12 on the third and sixth, but the other ranks add to 22 and 18, which are not the required multiples of four.
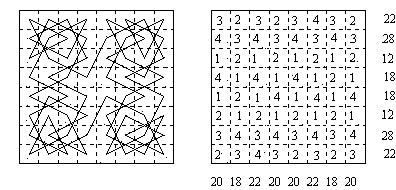
"Two chains (a, b, ...) and (a', b', ...) of equal length and forming parts of a single complete tour, are said to be contraparallel if a and a', b and b', ... each lie on the same column (or row) of the board, and if the knight traverses the two chains in opposite directions. The importance of contraparallel chains in the construction of magic tours is that a pair of these chains contributes a constant sum to each column (or row) concerned. Most magic tours can be analysed into an aggregate of contraparallel chains of lengths 4, 8, 12, 16 or 20 cells and can be so oriented that the constant sums of each pair of chains lie on the columns of the board. The only exceptions are magic tours 12d and 12h." To these we must now add the tours 01g and 01i. It is possible to analyse some tours into contraparallel chains in more than one way, and some can be analysed with corresponding cells in ranks or files. Where this occurs it is presumably best to choose the longest chains, or those closest together.
|
Table of contraparallel chains in 8×8 magic tours.
2(6): 01e, 03a 2(4): 05f, 16a, 23q, 27a, b, g, h, j, k, l, m, n, o, p, q, r, s 3(6): 00b, c, o5a 3(5): 01d 3(4): 00f, g, 23m, n 4(5): 01c 4(4): 03b, 14e 4(3): 00a, 01b, 03f, 14a, b, 23e, f, g, h, i, j, k, l, 27i, 34a, b, c, d 4(2): 00l, k, 12i, j, k, l 5(4): 12e, g, p, 23a, c 5(2): 23o, p, 25b 6(3): 00h, 03g 6(2): 01f, 12c, f, 14d, 23d, 25a, 27c, d, e, f 7(2): 00i, 01a, c, h, 05d, 12a, b, 34e, g 8(1): 00d, e, m, 03c, d, e, 05a, b, c, e, 12m, n, o, 14c, 23b The first number counts the pairs of contraparallel chains, the second (in parenthesis) counts the number of quartes in the longest chain. |
The above data is based on a more detailed table by Murray [1951 pp.21-23], to which analyses of the Marlow and Roberts tours have been added (but not the most recent discoveries, 00n, 00o, 07a, 14f, 27t).
The Marlow tour 03b can be analysed by ranks into the contraparallel chains 1–12/56–45, 13–16/64–61, 17–20/36–33, 21–24/60–57, 25–32/44–37 (longest chain 12 cells). However it can also be analysed by files into 1–8/60–53, 9–12/36–33, 13–28/52–37, 29–32/64–61 (longest chain 16 cells), so it is classified under 4(4) above. The Roberts tour 14e has the chains 1–8/60–53, 9–12/36–33, 13–16/64–61, 17–32/52–37 so is also in 4(4).
This analysis of Beverley's Tour and those similar to it is contained in Murray's 1936 article in The Problemist Fairy Chess Supplement and in his 1942 ms (ch.X pp.114-117) and in his 1951 ms (ch.I pp.3-4, ch.III pp.15-21) in different forms. As noted under the entry for Beverley (1848) in our History of Magic Knight's Tours, the analysis carried out here is essentially Murray's own work. We have no direct information from Beverley as to how he reached his solution.
"Let us begin by examining the first magic tour to be discovered. Beverley himself said nothing about the construction of his tour, but pointed out the special features: that it was magic, that the quadrants were also magic, and that the sum of the numbers in each 2×2 block was 130."
"If we divide the blocks into halves by vertical lines we obtain another feature which is significant, when we add up the numbers in each half-block. The 32 half-blocks alternately have totals 49 and 81. Beverley's tour is divisible into two pairs of contiguous contraparallel chains." [The contraparallel chains are said to be contiguous if a and a', b and b', ... are adjacent cells.] "One pair being 1–16 and 48–33" [adding to 49] "while the other is 17–32 and 64–49" [adding to 81] ".Using this construction, every column of a quadrant has sum 130, and every column of the board has sum 260."

"The critical half-blocks are those bearing the terminals of the contraparallel chains, 1 and 48, 49 and 32, 33 and 16, 17 and 64. The natural thing to do is to place 1 on a8 and 48 on a7. Now 49 is fixed: it must be on an '81' half-block and link with a7; it can only be on c6 and this means 32 on c5. Now there is a choice, 33 on a4 or e4: Beverley chose a4, which meant 16 on a3, 17 on c2 and 64 on c1. Thus the layout of the critical cells is possible, one on each row. The next step is to see what other numbers have fixed positions. Obviously 18 must be on a1 and this means 19 on b3, 20 on d4, 63 on a2, 62 on b4 and 61 on d3. Similarly 50, 51 and 52 must be on a5, b7 and d8 respectively and this fixes the positions of 31, 30 and 29. We now have three numbers in four rows of the half-board fixed and, mindful that the columns of the quadrants sum to 130, we look for the fourth number on these rows so that the rows of the quadrants may also sum to 130. To achieve this c4 must be 15 and c3 34, both are possible. In the upper quadrant we find that c7 must be 2 and c8 47. The left-hand half-board is now completed. The right-hand half-board is easily completed, having regard to the necessity that each row of the half-board should sum to 130. All the [loose] terminals of the chains on the left-hand half of the board lie on the d-column, and there are two ways in which these terminals may be connected with cells in the half-blocks on the right-hand half of the board to complete the tour. Beverley chose one (12a) and Wenzelides the other (12b), both completions being necessarily symmetrical with respect to the horizontal median. This makes it possible to substitute other symmetrical arrangements, provided the half-block system is abandoned. Four such arrangements exist: Jaenisch discovered 27c and 27d, Reuss 27e and Wihnyk 27f."

"As we have seen, Beverley exercised a choice between possible positions for the terminals of his contraparallel chains, one when he put '1' on a8, another when he put '33' on a4. There are in fact five different lay-outs which can be used, two with '1' on a8 and three with '1' on e8. The tours composed of two pairs of contiguous contraparallel chains are:" 27a, b, g, h, j, k, l. m, n, o, p, q, r, s. "All of these layouts can be completed in the same way that Beverley adopted but with the abandonment of the condition that every half-row must add to 130, since some of the half-rows will be 128 and others 132."
"There is also an easier way of obtaining these layouts, since the same numbers necessarily occur in the upper half of the board. We have only to arrange the chains 1–8 and 48–41 and the chains 25–32 and 56–49 on the upper half-board in such a way that both pairs are contiguous and the rows all sum to 260 to get all possible arrangements [18] for the upper half of the board. By subtracting each number from 65 we obtain all possible arrangements for the lower half of the board, and by combining the two halves so as to obtain complete tours, we obtain all the magic tours [14] of the Beverley class." [This method serves as a check on the enumeration.]
"This analysis deals with one kind of contraparallel chains and suggests that other sets of contraparallel chains might also yield magic tours, so I spent some time in investigating tours consisting of two pairs of 12-cell and two pairs of 4-cell contraparallel chains, and actually obtained twelve magic tours composed in this way. The method however proved to be very laborious and did not necessarily produce magic tours. I found later that the twelve tours which I had found had all been discovered before."
It is possible to construct other tours with the same contraparallel chains as the Beverley tour, but no longer adjacent. These are 05f, 16a, 23q. See Table in previous section.
Definitions of regular quartes (which occur in square, diamond and beverley forms) and ways of forming them into quads (4 by 4 blocks) which are then combined to form tours are given in the page on general theory of magic knight tours. It is shown that there are 45 regular quads in all. However, only 15 different quads occur in regular magic tours on the 8×8 board, so accordingly I diagram only those cases here.

THEOREM (Murray): The necessary and sufficient condition that a tour [8×8] composed entirely of
regular quartes shall have all rows and columns summing to 260 is that X = 60 and N = 20 for every row and column.
— "Proof: (1) If the quartes on a given
quarter-board are the x + 1, y + 1, z + 1, w + 1 quartes of the complete tour, then
the numbers on each cell of these quartes begin with 4.x, 4.y, 4.z, 4.w respectively,
this means that" [since each quarte has one entry in each row and column of the
quarter] "the first term in the summation of each row and column of the quarter is
4.(x + y + z + w) which we may write 4.Q. The same is true of each quarter, though the
value of Q may be different in each" [label them 11, 12, 21, 22] "but the sum of
the four values must be Q11 + Q12 + Q21 + Q22 = 0 + 1 + 2 + 3 + ... + 15 = 120."
— "(2) The n-terms of the numbers on the different
cells are so connected that a 1 on the top row occurs in conjunction with a 3 on the
bottom row and vice versa, and a 2 on the second row occurs in conjunction with a 4 on
the third, and vice versa. This means that the N-term in the summation of the two outer
rows is 10+a or 10–a in one and 10–a or 10+a in the other row. So also with
the two inner rows and the outer and inner columns. The row-sums for the whole board are
of the form 4.(Q11 + Q12) + 20 ± v "[with possibly four different values for
the variance v] ", with similar expressions for the columns. These forms are true of all
tours that are composed entirely of regular quartes, whether magic or not."
— "(3) If the tour is magic then all of these
expressions must equal 260" [which is 4×60 + 20] ". It follows first that v = 0
for every row and column, and so N = 20, and second that Q11 + Q12 = Q11 + Q21 =
Q22 + Q12 = Q22 + Q21, that is Q11 = Q22 and Q12 = Q21 "[i.e. the Q-values in
opposite quarters are equal] ", and so X = 60. [QED]"
The account in this section and the next is considerably condensed from Murray's explanation and the task described, when carried out manually, is much greater than he admits, but it can now be done by analogous computer methods.
"The simplest procedure for obtaining magic tours of regular quartes is to construct diagrams in which the terminals of the quartes are so arranged that every row and column has N = 20. Such an arrangement I call a matrix. All such matrices can be built up in the following way: Obtain all the [322] regular quadrants and above each column and by the side of each row add the excess or defect of its total from 10. Now examine each diagram to see if it can be used on quadrants of the upper half-board. To be usable, every terminal must link with a terminal in another quarte, either on the quadrant itself or on an adjacent quadrant" [unless end-points of the tour] ". Combine the usable quadrants in such a way that they can link and the defects and excesses of each row cancel one another. Collect together all these half-board diagrams that have the same run of defects and excesses. By combining these half-tours with the inversions of half-tours of the same class we obtain the matrices. If all the terminals on a matrix can be linked together so as to produce a knight's tour and if the cells of the tour when numbered in the order in which they are entered give for one row and one column the total 260, that tour is magic."
It is now known that there are 32 matrices possible for tours of regular quartes type, Murray found 30 of these and 2 others must be added to account for two of the Marlow tours, 01g and 23q. The matrices are listed here in a sequence that shows first those using squares and diamonds only, followed by those that also use beverley quartes. They are also listed according to the number of different quads used in the matrix. It happens that all those that use only one quad are all of squares and diamonds type, while those that use three or four are all of beverley type. The same quads may produce several different matrices according to the way they are arranged in the quadrants (not detailed here).
| List of Regular 8×8 Magic Knight Tours by Matrices | |
|
Squares and Diamonds Type
|
Beverley Type
|
| Total tours of regular type = 78; 34 of squares and diamonds, 44 using beverley quartes. | |
In constructing the matrices for regular tours Murray numbers the quartes 1 to 16: quartes 1, 5, 9 and 13 being in the a8 quadrant, 3, 7, 11 and 15 in the h8 quadrant, 2, 6, 10 and 14 in the h1 quadrant and 4, 8, 12 and 16 in the a1 quadrant. He numbers only the cells of entry and departure, underlining the cell of entry. This labelling of the quartes 1 to 16 should not be confused with the x-numbering of the quartes 0 to 15, which has yet to be determined.

"To determine the magic tours derived from this matrix: I begin by preparing a table showing all the ways
of connecting the end cells of each quarte with the beginning cells of other quartes."
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
-----------------------------------------------
3 4 1 1 2 1 1 2 11 12 6 5 2 1 2 1
5 6 2 2 3 4 9 10 15 16 8 7 15 15 10 9
15 16 6 5 7 7 9 9 16 16 11 12
13 14 8 8 10 10
11 12 13 14
16 15
"With the help of this table and a set of counters numbered 1 to 16 and a sheet of paper divided into columns
headed 0, 1 to 15 (to show the position of each quarte in a completed tour) I proceed to work out the permutations
of the sixteen counters and so obtain tours which are entered on the sheet of paper.
Three tours obtained in this way are:"
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
-----------------------------------------------
1 3 6 7 9 11 13 15 2 4 5 8 10 12 14 16 (1) closed
11 8 10 12 7 9 15 2 6 4 14 1 5 3 13 16 (2) open
13 15 10 12 14 16 1 3 2 4 5 7 9 11 6 8 (3) open
"We have now to test these formulae of tours to see if both rows and columns give X = 60. The row sum is obtained by adding the numbers in the heading which stand above the odd numbers in the formula, and the column sums by adding the numbers on the heading which stand above 1, 4, 5, 8, 9, 12, 13 and 16 in the formula of the tour. If both totals are 60 the tour is magic as its stands. If either total is not 60 the tour is not magic if the tour is open, but if the tour is closed it may be magic with a different starting point, and the effect of changing the starting point must be examined. A convenient way of doing this is to use a strip of paper with the numbers 0, 1, ..., 15, 0, 1, ..., 15 which can be placed over the heading and moved so that any desired column may be 0, i.e. the starting point of the tour. The effect of shifting this strip one column to the right or left is to increase or decrease the sum of any eight terms in the formula by 8. No change of starting point can make the sum 60 unless the original total was 60 ± 8n. Unless the row and column sums are both an even or both an odd number of 8s from 60, no change of starting point can bring them simultaneously to 60."
"The row and column sums for the above tours are (1) closed 36 and 68, (2) open 65 and 70, (3) open 60 and 60. It will be seen at once that (3) is magic and (2) not. The closed tour (1) is not magic with the given starting point but both sums are of the form 60 ± 8n and in both cases n is odd, so other starting points must be tested. To convert 36 to 60 three shifts are necessary, so I move the strip until 0 covers 5. Now both row and column sums are 60, so the tour is magic provided it starts from quarte 11. Since a closed tour may have several starting points I next try the effect of seven shifts, but this brings the row sum to 76, and as the matrix is in diametral symmetry there is no need to try more than eight shifts."
The term "irregular" as defined in the page on magic knight's tours in general, simply means that the quartes used are not of the "regular" type (i.e. squares diamonds and beverley type). The tours themselves show just as much regularity, in the usual sense, as regular tours.
It is helpful to classify the irregular 8×8 tours according to their increasing number of irregular quartes. Murray stated that regular quartes must be contraparallel to regular quartes and irregular to irregular, and that the number of each type must be a multiple of four, however the new tours 14e and 14f break the multiple of four rule.
The eight cells used by a pair of beverley quartes may be combined differently to give a pair of semiregular quartes in the following three ways. Only the first of these is mentioned by Murray, since it is the only type occurring in 8×8 magic tours; but the others may be usable on larger boards.
"The use of irregular quartes" [of type (a)] "was first shown by Charles Bouvier in 1876 (05a) and two other tours with these quartes were discovered later by C. E. Reuss (00j) and M. Wihnyk (27f)."

"The conditions under which this substitution may be made without destroying the magic feature are: (1) The tour must include two pairs of beverley quartes in the same half of the board and symmetrically placed with respect to the shorter median of that half-board [the half-blocks used being parallel to that median]. (2) If in the tour one pair of beverley quartes are the quartes numbered m and n in the tour, and m' and n' are the other pair, m being symmetrical to m' and n to n', then we must have m + m' = n + n' = 15. The replacement of the beverley quartes by the irregular quartes as in (d) then leaves the resulting tour magic. " [The overall effect of the change is an interchange of four pairs of numbers.] "The tours of this type, 00j, 05a, 27f are related in this way to the tours 00d, 05e, 27d respectively (strangely 05a, with irregular quartes, was discovered before 05e, with beverley quartes)."
The tours with 4 irregular quartes are the three semiregular tours listed above plus Murray's four tours of Beverley type 27g, 27h, 27n, 27o, which have both pairs of chains in the same half-board, and Lehmann's 16a and the new 07a from Mackay et al, in which the contraparallel chains are in different half-boards. In 16a and 07a two lines have X = 61, N = 16 and two have X = 59, N = 24.
The only tour with 6 irregular quartes is the new Roberts tour 14e which nevertheless has normal values X = 60, N = 20 in all lines.
The tours with 8 irregular quartes are 01i, 12c, 12d, 12f, 12g, 12h, 23o, 23p, 27e. The pairs 12f, 23o; 12d, 12h; 12c, 23p have the same matrices (i.e. the same arrangement of both regular and irregular quartes). In 01i, 12d and 12h two row-sums and two column-sums are X = 59, N = 24 and two X = 61, N = 16.
The only tour with 10 irregular quartes is the new Mackay et al 14f which nevertheless has normal values X = 60, N = 20 in all lines.
The tours with 12 irregular quartes are the newly found Mackay et al tours 00n, 00o and 27t.
The tours with all 16 quartes irregular are the seven 00l, 00k, 01e, 12i, 12j, 12k, 12l, all with different arrangements of the quartes, five of which are in biaxial symmetry, the exceptions being the cyclic tours 00l, 00k which have one axis of symmetry.
A semi-magic tour is a rectangular tour that adds to a constant sum in every line in
one direction, but not in every line in the perpendicular direction.
A quasi-magic tour is a semi-magic tour in which the non-magic lines add to only two different values.
A near-magic tour is a semi-magic tour in which the perpendicular lines add to the magic constant and two other values.
A demi-magic tour is a tour adding to two constants in the ranks and the same two constants in the files.
It is natural to study tours of these types in the case of boards that do not admit tours to be magic in both ranks and files, or on which no such magic tours have been constructed.
Examples, previously listed on separate pages, are now been moved to the 6×6, 10×10, and larger square sections, and to the section on oblong boards.