
Logically one would expect patterns formed of simple lateral and diagonal moves to have been studied before those, such as knight's tours, that use skew moves. This is in fact the case, though generally they have appeared not explicitly as tours but disguised as labyrinths or as elements in artistic designs.
Non-intersecting rook tours are implicit in 'boustrophedonal' writing, found in early Greek inscriptions, running from right to left and left to right in alternate lines, in imitation of ploughing [Brewer's Dictionary of Phrase and Fable 1974, p.142]. The ploughing of a field is in effect a rook tour. The plough was used in Mesopotamia around 3500 BC [Barraclough & Stone The Times Atlas of World History 1989, p.16]. Slightly more elaborate rook tours are seen in the wave-like patterns which are common as borders in Greek art. The 'meander' pattern, shown as a wazir tour in diagram 2(b) below is so named from the winding course of the river Maeander in Phrygia (part of modern Turkey). Similar winding courses are to be seen in many rivers in low-lying areas. The Cuckmere near Seaford in Sussex provides an English example.

Spiral labyrinths and dances are also ancient. The term labyrinth is used for designs in which there is a single path to follow; as opposed to puzzle paths, called mazes, with branching paths and dead ends, which were a Renaissance innovation (~1550). Rock-carved labyrinths are known from as far apart as Arizona, Sumatra and Scandinavia, but their dates are disputed [Nigel Pennick Mazes and Labyrinths 1990]. All however are of similar design to the legendary labyrinth at Knossos, as represented on Minoan coins (~1600 BC). The pattern of the classical labyrinth is formed by bending and stretching a double meander round in a circle, as illustrated here.
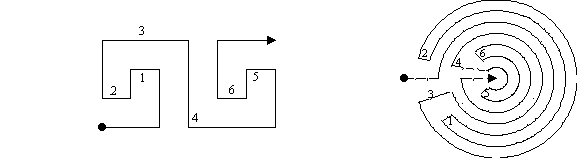
Greek myth attributes the design of the Minoan labyrinth to the proto-engineer Daidalos, who is also mentioned by Homer as maker of a 'choros' for Ariadne, which was a circling dance, or a place for dancing [Liddell & Scott, Greek-English Lexicon, abridged 1935, pp.148, 786]. The prefix 'Dai-' is said to mean cunning or curious and 'Alos' is a furrow, so perhaps his very name means 'labyrinth'. Pennick (1990) attributes the discovery of the topological equivalence illustrated above to Jeff Saward in lectures given in 1981-2, however Brewer (1974, p.698) states that the Maeander "is said to have given Daedalus his idea for a labyrinth" so knowledge of the property can probably be traced to earlier sources (if indeed it was ever lost).
During the middle ages the classical labyrinth design was elaborated. An early example is the pavement labyrinth in the Church of San Vitale, Ravenna (~530). The underlying wazir tour is shown below the labyrinth diagram.

The famous pavement labyrinth at the Cathedral of Notre Dame, Chartres (~1250) is even more elaborate. The same design as that of Chartres occurs at St Quentin and Amiens (1288) and is extended further in the plan for the Town Maze on the common at Saffron Walden (~1400).
For more on labyrinths and mazes see H. E. Dudeney, Amusements in Mathematics (1917) pp127=137.
A version of this article appeared in The Games and Puzzles Journal #15, 1997, pp.249, 262-3.
One of the main characteristics of 'Celtic Art' during its later period is the use of interlace patterns depicting a ribbon passing alternately over and under itself. No doubt such patterns derived originally from depictions of real interlacings, as in the plaiting of hair, rope-making (where several strands are woven together to give greater strength), lace fastenings for boots, leggings or coats, or in the passes and stitches used in weaving, tapestry and embroidery.
Many interlacings can be represented graphically by a path of king moves on a lattice of squares, the cross-overs being made by diagonal moves of the king, though this does not necessarily imply that they were designed this way. Diagrams follow of several examples in which these underlying king paths are in fact tours or pseudotours. It may be noted that these king tours avoid sharp turns (of 45°) since this would result in small interstitial areas, not allowing room for the definite width of the ribbon.
These are found in books and artefacts produced in monasteries of Ireland, Scotland and Northern England. We consider them here in order of increasing complexity, not necessarily chronologically.
The cover of "A strange object known as the soiscél Molaise … made around year 1000 as a cumdach or book-shrine for the Gospel of St Molaise, using pieces of a house-shaped shrine of the early eighth century" [Lloyd and Jennifer Laing Art of the Celts 1992] uses various interlacing patterns to fill gaps in the design. Among these are patterns that may be represented by king paths on 2×6, 6×6 and 6×14 boards. Obviously the first is a simple plait. The second is a 'prime knot' in the modern topological theory of knots. The third is a pseudotour, consisting of two linked circuits.

Similar but more elaborate designs are used in the upper and lower borders on a page illustrating an Eagle symbol in the Book of Dimma, late 8th century, and in the left and right borders on the Lion symbol page of the Book of Durrow of the mid 7th century [Laings 1992]. These can be simplified to pseudotours 4×28 and 4×34, which may have been the basis for the designs.
A nearly square king tour underlies the design of a panel from the Saint Madoes stone, Perthshire [George Bain Celtic Art, The Methods of Construction Constable, London 1951]. This is a 20×24 king tour, which can be formed by 'doubling' a simpler king tour 10×12 and altering some links to turn the pseudotour into a true tour.

The 'binding knot' from the Book of Kells, late 8th or early 9th century is possibly the most elaborate of these designs. [For full reproductions of the Book of Kells knot see Pennick (1990, p.45) and Bain (1951, p.46)]. By redrawing the design on squared paper, I found that this knot becomes two circuits of king moves, on a board in the shape of a quadrate cross (formed of thirteen 8×8 squares).
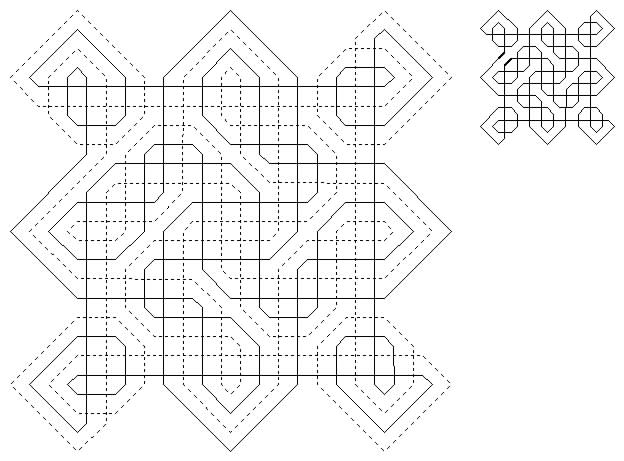
The following quotation from Alcuin (735-804) is perhaps what the design illustrates: "the four rivers of the virtues flowing out of one bright and health-giving paradise, irrigating the whole breadth of the christian church" [Laings 1992]. Examination of the knot shows that the two threads of which it is constructed follow each other in parallel throughout, thus the pair of threads define a single path. Replacing the two king paths by one line midway between them results in a single king tour of a quadrate cross formed of thirteen 4×4 squares, as shown in the smaller diagram. This cross tour explains why the threads come to a point at the four cardinal points instead of just curving round: they correspond to the corners of the square part of the quadrate cross. It seems evident to me that in this case at least the king tour was consciously the basis of the design of the Kells knot.
Another context in which interlacings like king tours can be seen is that of change-ringing. This is a method of ringing four or more bells, each tuned to a different pitch, so that a different sequence of notes is followed each time the full set of bells is rung. The simplest pattern in which four bells can be played, known as 'plain bob minimus', is shown in the diagram. The highest pitched bell 1 'hunts' through the other bells to the back, stays there one more change, then hunts forward again to the front. Eight different sequences are thereby rung. (Joining 1-2 and 3-4 in the final column and 2-3 in the first column gives a king tour.)
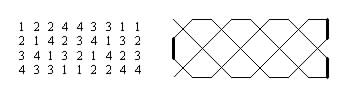
More elaborate change-ringing schemes were designed by Fabian Stedman (b. 1631) who wrote two books, Tintinnologia and Campanologia. [Reference: M. Darton and J. Clark, The Dent Dictionary of Measurement, 1994, pp. 67-8.]
A 'knot' in mathematical terms is a closed curve in three-dimensional space. If one knot can be deformed so that it is congruent to another without passing through itself anywhere, the two knots are of the same type. In particular a knot that can be simplified into a circle is a 'trivial knot' (or an 'unknot'). It is by no means always obvious that a given knot is an unknot, as example (A) shows. I show the knots as king paths, with the intersections arranged diagonally, the heavy line passing over the lighter line. Presenting the knots in this formalised way may perhaps give clues to classifying them or analysing their structure. They are not all complete tours.

A 'compound' knot is one formed from two knots by deleting a small part of each knot and joining the ends in such a way that the joining lines do not cross each other or any parts of the existing knots. A 'prime' knot is one that is not formed by joining two knots in this way. A knot can be classified by the minimum number of crossovers in a representation of it. The numbers of prime knots P(n) of 0 to 13 crossings are: P(0) = 1, P(1) = 0, P(2) = 0, P(3) = 1, P(4) = 1, P(5) = 2, P(6) = 3, P(7) = 7: These cases are illustrated above. [The series continues: P(8) = 21, P(9) = 49, P(10) = 165, P(11) = 552, P(12) = 2176, P(13) = 9988. The totals do not count reflected knots as different. P(11) is due to Alain Caudron 1978, P(12) and P(13) to Morwen Thistlethwaite, 1981 and 1982. Reference: Colin C. Adams The Knot Book subtitled An Elementary Introduction to the Mathematical Theory of Knots (W. H. Freeman and Co, New York, 1994), pp.24, 281.]