
If we regard a cell passed through in two different directions as 'visited' then we find some distinctive tours by 'riders', such as rook, bishop or queen, become possible. These are not strictly speaking 'tours' in the same sense as knight or king tours, since they may pass through some cells twice. These results were previously shown on the page now devoted to rook tours.
The material on Hoppers is based on that included in the 2019 PDF #2 on Walker Tours.
The clockwork mouse tour is a particularly distinctive rook crossover tour and was one of my own earliest tour discoveries, made on 23 July 1973, and published in Chessics (#10 p.7 1980 and #11 p.11 1981), although I was later surprised to find the pattern has a much older pedigree.
A clockwork mouse (otherwise known as a rotating directed wazir) faces in a definite direction (North, South, East or West) and moves one step at a time directly forward, or turns where it stands to face 90° to the right or left. This rotation counts as a move. These moves can be shown simply by stating the new direction that the piece faces after the turn.
The puzzle is to place a clockwork mouse anywhere on the chessboard, wind it up and allow it to wander round the board in such a way that it spends the same amount of time (i.e. number of moves) in every cell, and ends up where it started (facing in the same direction). Surprisingly, the path is uniquely determinate.
A group of assorted games pieces of distinctive design were discovered in the bay of Uig in the Isle of Lewis in Scotland in 1831 and dated to the 12th century. In an illustration to an article by Rodolfo Pozzi (1998, Fig 11), copied to me by Mike Pennell, the back of one of the Lewis chess pieces, a queen, is decorated with the pattern of a rook 8×8 crossover tour. This pattern, rotated 45°, is shown in Celtic fashion as a ribbon going alternately over and under itself, the bends being rounded rather than angular. A similar 4×4 version also occurs on the chair of a king. A similar design based on a 5×5 board with two corner cells omitted is found, rotated 45°, on Tuvinian rook and king pieces described by Pozzi.

The following items appeared in The Games and Puzzles Journal issue #31, Jan-Feb 2004 having previously been presented as puzzles for solution in issue #30, Nov-Dec 2003.
Siep Korteling e-mailed on 10 May 2003: "I maintain a website http://www.dorinde.nl/steenslag on International Checkers problems. In that game, played on a 10 by 10 board, a solitary king behaves just like a bishop. I am looking for the shortest path for a king (bishop) to travel all the black fields in a 10 by 10 checkerboard, where moving over a field counts for 'hitting' a field. Could you point me the way?" In subsequent correspondence we found that the answer depends on how a 'path' and its 'length' are defined and what counts as 'visiting' a cell. It is impossible to make a 'tour' that enters or passes through each cell once: some cells must necessarily be visited twice. We have found solutions for four distinct cases.
THE PROBLEMS Find the shortest path for a bishop to visit all the black cells on (A) an 8 by 8 and (B) a 10 by 10 board, for the following cases: (a) minimise number of bishop moves, (b) minimise distance travelled by the bishop, (c) minimise number of moves times distance, (d) minimise number of moves when 'visiting' a cell means either stopping there or passing through it twice. In each case we require that the bishop completes each straight section of the path before turning, and that there be only one route along the path under this condition.
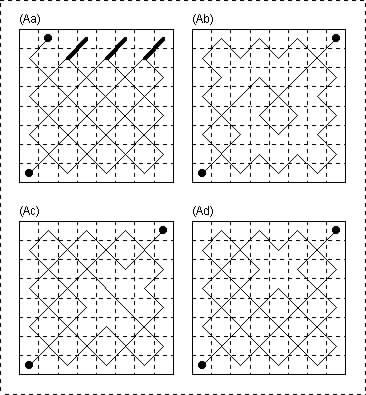
SOLUTIONS (A) 8×8
(Aa) Solution by Siep Korteling.
11 - 88 - 77 - 86 - 31 - 13 - 68 - 57 - 84 - 51 - 15 - 48 - 37 - 82 - 71 - 17 - 28 which takes only 16 moves (geometric length 49√2).
(Ab) Solution by George Jelliss.
11 - 33 - 15 - 26 - 17 - 28 - 37 - 48 - 57 - 68 - 86 - 75 - 84 - 73 - 82 - 71 62 - 51 - 42 - 31 - 13 - 46 - 64 - 53 - 44 - 88. Length 35√2 (25 moves).
(Ac) Solution by Siep Korteling.
11 - 44 - 17 - 28 - 82 - 71 - 53 - 31 - 13 - 68 - 86 - 75 - 84 - 51 - 15 - 48 - 66 - 88 Moves 17, Length 43√2
(product = 731&radic2) as compared with 784√2 in (a) or 875√2 in (b).
(Ad) Solution by H. E. Dudeney.
11 - 55 - 82 - 71 - 17 - 28 - 46 - 13 - 31 - 86 - 68 - 57 - 48 - 15 - 51 - 84 - 66 - 88.
This solution to a bishop tour of the black cells of the 8 by 8 board in 17 moves (geometric length 45√2)
was given by H. E. Dudeney in The Tribune (Dec.3 1906), and in his Amusements in Mathematics (1917 problem 325),
and is reported in W.W.Rouse Ball, Mathematical Recreations and Essays, (1956 edition page 187).
However the above results show this route is not minimal in the number of moves (as seems to be implied by the context of Ball's work)
nor is it the geometrically shortest length. In his 1917 text Dudeney specifies that "You can visit any squares more than once,
but you are not allowed to move twice between the same two adjoining squares." This shows how carefully problems must sometimes
be phrased to eliminate alternative solutions. If it takes the bishop one second to pass through a cell and one second to make a
right-angled turn then, apart from the initial and final cells, he spends the same amount of time in every cell.
In the 2019 PDF it is noted that the solution (Ab) in 25 moves with length 35 units, copied below, is also possible in a symmetric solution.

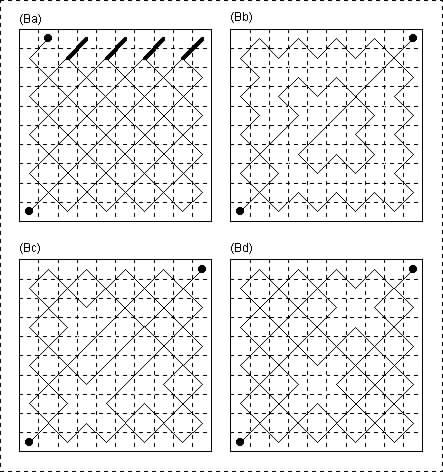
SOLUTIONS (B) 10×10
So that each cell on the 10 by 10 board is represented by two digits we write 10 = a.
(Ba) Solution by Siep Korteling.
11 - aa - 99 - a8 - 31 - 13 - 8a - 79 - a6 - 51 - 15 - 6a - 59 - a4 - 71 - 17 - 4a - 39 - a2 - 91 - 19 - 2a. Taking 21 moves (geometric length 81√2).
(Bb) Solution by George Jelliss.
11 - 33 - 15 - 26 - 17 - 28 - 19 - 2a - 39 - 4a - 59 - 6a - 79 - 8a - a8 - 97 - a6 - 95 - a4 - 93 - a2 - 91 - 82 - 71 - 62 - 51 - 42 - 31 - 13 - 46 - 37 - 48 - 57 - 68 - 86 - 75 - 84 - 73 - 64 - 53 - 44 - aa.
Length 53√2 (41 moves).
(Bc) Solution by Siep Korteling.
11 - 33 - 15 - 37 - 19 - 2a - 48 - 6a - a6 - 84 - a2 - 91 - 73 - 51 - 42 - 31 - 13 - 8a - a8 - 53 - 71 - a4 - 4a - 17 - 44 - aa.
Taking 25 moves, with geometric length 67√2. The product is 1675√2 as compared with 1701√2 for (a) and 2173√2 for (b).
(Bd) Solution by George Jelliss.
11 - 44 - 17 - 4a - 68 - 13 - 31 - 53 - 71 - a4 - 77 - 55 - 19 - 2a - a2 - 91 - 64 - a8 - 8a - 79 - 6a - 15 - 51 - a6 - 88 - aa.
Taking 25-moves (geometric length 73√2.
COMMENTS (C): Here are some generalisations. On a board of side 2h the bishop lines form h components, consisting of the diagonal path and h−1 rectangular paths, comprising 4h−3 moves, of total geometric length (2h−1)2√2. It is possible to make a 'unicursal tour' of these lines (i.e. to draw them in a continuous pencil stroke) since there are only two odd nodes (the ends of the diagonal). If we try to minimise the number of straight moves of the pencil in this tracing each rectangular circuit takes at least 5 moves and to connect each of these to the diagonal requires h−1 breaks in the diagonal, making h diagonal moves, giving the minimum 6(h−1) + 1. This sequence runs: 1, 7, 13, 19, 25, 31, 37, ...
(Ca) If we have to visit all cells but not all branches we can reduce the number of moves for each circuit to 4 by making the breaks at their corners. The procedure as for (Aa) and (Ba) then leads to a solution in (5h−4) moves (i.e. the 4h−3 plus h−1 switchbacks), with total geometric length still (2h−1)2√2, since each of the h−1 circuits has one √2 step removed.
(Cb) To minimise the geometric length. The problem as stated is soluble on boards with h = 4k or 4k + 1 (including the trivial 2 by 2 board), but to become solvable, in a uniquely defined path, on boards with h = 4k + 2 or 4k + 3 switchbacks must be allowed.
(Cc) This is solved by a method similar to (Cd) but making the deleted rectangles as large as possible.
(Cd) Looking at a diagram of the Dudeney tour (Ad) I noted that it is based on a line 11 - 88 from corner to corner and three rectangular circuits, from each of which one single-step bishop move has been deleted. These four deleted moves form a small circuit, namely 55 - 46 - 57 - 66 - 55. The same method doesn't quite work on the 10 by 10 board since there is one diagonal 11 - aa and four rectangular circuits, so that at least five deletions are needed. My 10 by 10 solution uses eight deletions forming two small circuits. We can make 4 by 4 and 6 by 6 solutions possible by allowing switchbacks. On a 32 by 32 board a solution is possible by deleting five small squares: {(3,3), (4,4), (5,3), (4,2)}, {(11,3), (12,4), (13,3), (12,2)}, {(19,3), (20,4), (21,3), (20,2)}, {(27,3), (28,4), (29,3), (28,2)}, {(15,9), (16,10), (17,9), (16,8)}. The first four join up the rectangles and diagonal in sets of four, and the last joins up the four resulting paths. (81 moves).
According to my notes the 14-move 'Queen Tour' Problem on the 8×8 Board was first presented by Sam Loyd in Le Sphinx March 1867, with the first solution shown below. One month later the Illustrated London News solution appeared (probably by H. E. Dudeney as it is the solution he gives in Amusements in Mathematics p.99 (but rotated 180°). All three solutions were shown by T. R. Dawson (Problem 194 in his "Echecs Feeriques" column in L'Echiquier Dec 1930 p.1149 and 1249). The third solution is the best in my view since it has no K-type junctions which are both visited and passed through. I found this solution myself, independently, but later found that Dawson has the priority.
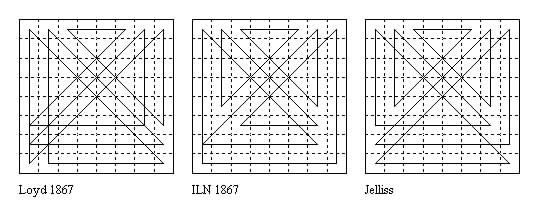
A version in Loyd's Puzzle Magazine, April 1908 (#46 in Mathematical Puzzles of Sam Loyd by Martin Gardner, Dover 1959) starts the piece in the middle of a side (d1 or a5) in which case to pass through all cells in 14 straight moves and return to the start is impossible in queen moves. The solution in 14 moves given uses two nightrider lines, and one cell is visited twice.
The simple 15-move non-intersecting open Queen Tour from c6 to f3 was used in a puzzle by H.E.Dudeney in The Tribune 3 Oct 1906, and later problem 70 in The Canterbury Puzzles.
The Bouncer, invented by Peter Wong, moves along Queen lines until it reaches an edge of the board it then bounces straight back along the same line to twice the distance, measured from the centre of an imagined cell beyond the board edge. (It can also bounce off pieces, which makes it a sort of hopper, but that property is not used here.) The cells cf36 cannot be reached.
The 60-cell tour problem was proposed by Peter Wong (Variant Chess #3 Jul-Sep 1990 p.31. Solutions in #4 Oct-Dec 1990 p.47). The Wong tour is asymmetric and uses only three diagonal moves (12-13, 48-49, 60-1). The Jelliss tour is quatersymmetric and uses 16 diagonal moves.
Grasshopper Over Fixed Hurdles
The Grasshopper moves along queen lines to the cell beyond a hurdle. F. Cassani (Die Schwalbe Aug 1931, cited in Chessics #15 p.7 1983) shows 16 maximumming moves over five fixed hurdles. The G starts and ends at a1. T. R. Dawson (FCR Aug 1950 prob 8755) gave a grasshopper 39-move open tour over 24 fixed hurdles. The G starts at a1 and ends at h6. Each move, including the long move 20, being the mimimum possible to an unused vacant cell. This problem was set by Dawson 23 years previously in Chess Amateur (Jan 1927) but he wrote in 1950: "The reason I did not publish the solution in CA is because I solved it only a month ago". The stipulation of the problem asked for the "fewest stops ... no stop being used solely to fill a square".
T. W. Marlow ('Grasshopper Gallery' Chessics 1983 #15 p.6-7 prob 567, solutions in #16 p.5) proposed the task of placing 2 to 5 hurdles so the G can visit as many cells as possible in as few moves as possible. With 2 blocks he finds 6 moves. However his other solutions allow cells to be visited twice. Without this 3 blocks allow 17 moves, 4 blocks allow 23 moves.
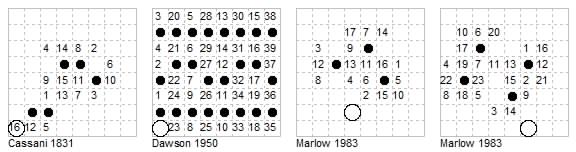
A similar problem but with the condition that each hurdle be used once only was proposed by G. Leathem (FCR Dec 1939 prob 3976). A complete tour of the 8×8 board under these conditions is impossible, since the number of cells used must be odd (initial cell of grasshopper and two for each hop). Dawson found 31-move solutions omitting one cell (FCR Feb 1940 and 1945), and also two closed solutions (which omit two cells). These are not shown here.
Vaclav Kotesovec Dual-free Leaper and Hopper Tours, Prague 2009 gives new results (reviewed by John Beasley in 'Grasshopper Tours' Variant Chess: #61 Jul 2009 p.115). For the Dawson task, without the minimummer condition, he finds a 52-move open tour over 11 hurdles and a 52-move closed tour over 12 hurdles. These are claimed to be computer proven maxima.

Grasshopper over Knight.
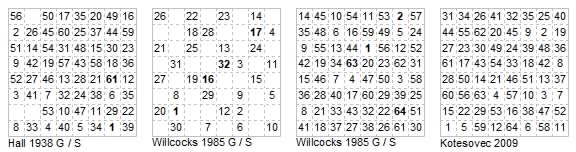
The problem of a grasshopper tour over a knight as moving hurdle was raised by S. H. Hall (FCR 1938 prob 3107). He achieved a 61-cell open path (shown below). A 64-cell tour was considered impossible, but the problem was finally solved 50 years later by T. H. Willcocks (Chessics #23 1985 p.84) with two open tours. Closed tours formed in this way are termed by THW as cyclic if the hurdle's journey is also reentrant, since then the hopper can get back to where it started and the whole tour can be repeated. The second diagram below shows a cyclic 32-move tour with rotary symmetry. T. H. Willcocks explained in Chessics that his method of finding solutions was to construct tours of 16 cells, cyclic if possible, and then combine them into 32 and then 64. The third diagram shows his 64-cell open tour that includes a 62-cell cyclic tour (cells 2 to 63). Recently Kotesovec has found a 64-cell closed tour. The challenge of a full cyclic tour remains.
Grasshopper over Rook
The problem of grasshopper over rook tour was solved by T. R. Dawson (FCR Apr 1938 prob 3179). Dawson started Ga1 Rb2. Beasley (VC 2009) renumbers to start Ga7 Rb2 to make clear the repeated 16-cell pattern.

Grasshopper over King
The problem of a grasshopper tour over a king as moving hurdle on the 4×4 board was proposed by P. C. Taylor (PFCS Oct 1930 p.8 prob.45). Ten cyclic solutions were given, all starting and ending with Ga1, Kb1. A cyclic symmetric 8×8 solution, combining four 4×4 solutions, was given years later by C. M. B. Tylor (Chessics #5 1978 p.8). Diagram above. Ga6 Kb5.
Moose over Moose
C. M. B. Tylor Chessics #5 p.7 Jul 1978 found an amusing moose over moose tour. In this the pieces do not move alternately. Sometimes, as in the corners, one moose makes two successive hops. Each moose covers 32 cells. In effect each hop is a knight move made up of a fers followed by a wazir move, or vice versa, the other moose occupying the cell passed over. No long-distance moose moves are used. The moves of the first moose are shown. The other starts at c5. Both follow the path illustrated The c4 moose uses the cells aceg3478 and bdfh1256. The c5 moose uses the other 32 cells.

Nightriderhopper Over Rook
This piece was investigated by T. R. Dawson and F. Douglas in Chess Amateur Aug 1928, looking at paths of NRH over R. They gave a shortest closed path of 8 moves, and a longest closed path of 56 moves (some cells are entered twice).