By bending boards round so opposite edges come together pieces acquire extra move-patterns due to being able to pass across the edges. A circular board m×n is an array of cells consisting of m concentric circles of n cells each. Thus the ranks circle about the centre point and the files are radial. Various tours have historically been constructed on 8×8 and 4×16 circular boards, and the 4×16 board in particular has been used for a distinctive variant of chess. A cylinder board is a rectangular board in which the left and right edges are considered to be contiguous as if the paper were bent round to form a tube. This is also described as a vertical cylinder. If the top and bottom edges are instead taken to be contiguous we have a horizontal cylinder. There is no real difference between cylinder and circular boards as regards the way moves connect the cells. They are just differently presented to view. If both pairs of edges are identified the board becomes a torus.
Boards with one or both edge-connections given a twist can also be considered, resulting in boards of Moebius Strip, Klein Bottle and other designs. Spherical boards have also been played with, where edges reduce to a point, though it is not always clear how pieces move when they pass across the poles. These boards however are beyond our current remit. See for example G. Cairns Mathematics Magazine (vol.70 #3 Jun 2002) 'Pillow Chess'. This is about a type of spherical chess and the bibliography has 81 references. [online]
This page has been revised October 2022 to reflect the treatment of the subject in the 2019 PDFs. It incorporates the Torus Tours page published (August 2009) based on items in Variant Chess #58 (October 2008). The Quasi-magic 4×4 tours are from November 2012. The section on 'Natural Magic' duplicated the treatment now given in the 'Theory of Magic' page.
Sections on this page:
— Bent Boards
— Circular Boards
— Cylindrical Boards
— Toral Boards
— The Step-Sidestep Method
— Five-Square Magic Torus Tours
— Seven-Square Magic Torus Tours
— Eleven-Square Magic Torus Tours
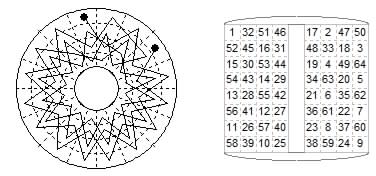
The earliest example of a tour on a circular chess board is undoubtedly that given by Richard Twiss in volume 2 of his Chess (1789).

He describes a manuscript from the Cotton collection in the King's Library in which is a drawing of a round Chess-board (in effect a 4×16 rectangle bent round so the ends meet). "The figures on this board (in the plate) show the march of the Knight in order to cover the sixty-four squares in as many moves. This I found after four or five hours trial on a slate at different times; it probably has never been done before, and will be found much more regular than any of the like marches on the square board." [details from Ken Whyld] Twiss shows the tour in numerical form on a circular diagram. It is shown above in graphical form, which makes the regularity much clearer. Alongside we show the same tour in numerical form in a conventional representation.
Articles by John D Beasley in Variant Chess on 'Circular Chess in Lincoln' (#31 p.33-34, 48 and #32 p.55) give the Twiss tour as above and two new tours, and he notes that "on a circular board we can achieve a symmetry impossible on an ordinary rectangular board"
The first tour is formed by a systematic forward and across repeated movement. The pattern has two 'centres' midway between 22 and 43 and between 59 and 6. Working outward from these centres the opposite numbers are complements adding to 65. The second tour is a sort of zigzag step-sidestep tour with 1 and 64 diametrically opposite. The centres are between 20 and 45 and 41 and 24 (crossed by the middle move 32-33).
The natural numbering of a rectangular board can be regarded as formed by a series of wazir moves on a cylinder board, with a fers move interpolated whenever the next wazir move would enter an already used cell. This is an example of a tour by the step side-step method discussed further in the Torus section below. The partially magic properties of the natural numbering are discussed on the Theory of Magic page.
Knight's tours on cylinder boards were considered by S. Vatriquant in L'Echiquier (Sep 1929 p.414-415), where he gave schemes for tours on boards of 2, 3 and 4 ranks.
The knight's moves on a strip 2×n form a braid of four strands. However if we join the two ends of the board to make a cylindrical strip the number of strands reduces to one or two depending on whether the board is of odd or even length, so in the odd cases we get closed tours, surprisingly including the case n = 1. To visualise the moves it is helpful to draw the squares on a larger scale.

The 3×3 diagonal magic square can be interpreted as an open knight tour on a cylinder board, in either orientation, as illustrated.
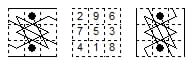
However a closed tour (not magic) is also possible, since where the edges are joined the chequering is violated and the knight can move to a cell of the same colour. The 3×3 tour by Vatriquant can also be toured, with the cells visited in the same sequence, by taking the board to be a horizontal cylinder.
On 3×n cylinders the tours can be of any length. Vatriquant used a repeated cycling pattern of three moves that will suffice to tour a 3×n board of any length.

We show also a 4×9 cylinder with a closed knight tour by S. Vatriquant. Analogous tours are possible on any cylinder boards 4×n with n odd, including 4×1.
Camel tours on the 8×8 cylinder were considered by Frans Hansson (Problemist Fairy Chess Supplement Apr and Jun 1933, problem 714). "On the 8×8 cylinder, ah files joined, trace a closed diametrally symmetrical camel tour in 32 moves containing two 7-unit lines, one with endpoint at a1, the other with endpoint at h8." D. H. Hersom found the second solution shown.
When numbered 1 to 32 from d6 to e3 these tours have diametrally opposite cells adding to the constant value 33 (not a constant difference). This is what we have called 'negative symmetry', though only the first tour has a Bergholtian crossover at the 'centre'. Of course on a cylinder board there is a centre line but no actual centre point. The Hersom tour crosses the centre line at two 'diametrally opposite' points of the cylinder.
Boards with both pairs of opposite sides joined form a torus. (A torus board is also termed a double cylinder, anchor ring, doughnut or pretzel by various writers.) We begin by looking at some results concerning even-sided boards.
On a 2×2 board one would naturally suppose that the only moves possible would be wazir and fers steps. However, Dr C. M. B. Tylor (Chessics #14, 1982, p12, problem 500, posed the problem: "How many geometrically distinct knight tours are possible on a 2×2 torus?"
There are eight possible knight moves from a1, four lead to a2 and four to b1; they are equivalent to wazir moves, but follow different paths. Two of the a1-a2 moves pass round the board cylindrically, while the other two cross both pairs of joined edges. Dr Tylor found that there are 17 different knight tours on the 2×2 torus, and that there are 8 different types of symmetry involved.
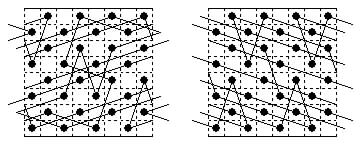
If the boards are expanded to form a lattice they come into 7 of the 17 possible two-dimensional space groups (i.e. wall-paper patterns). The following are diagrams of the tours in this expanded form; any four squares within the pattern form a representation of the tour.

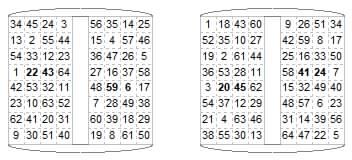
In an note rediscovered in November 2012 I made a search for magic knight tours on the 4×4 torus, considering 40 configurations of the first 8 moves, but concluded that such a tour was impossible. Relaxing the conditions, the best that I found were some quasi-magic tours, adding to 34 in the files and to 30 or 38 in the ranks, three open tours and two closed:
01 04 15 10 01 04 15 10 01 14 05 10 01 06 13 10 01 14 05 10 06 09 02 13 16 07 02 13 06 09 02 13 14 09 02 05 06 09 02 13 11 14 05 08 05 14 11 08 11 04 15 08 07 04 11 16 15 04 11 08 16 07 12 03 12 09 06 03 16 07 12 03 12 15 08 03 12 07 16 03
This tour (added here December 2012) appears in the Twentieth Century Standard Puzzle Book (1907) edited by A. Cyril Pearson. The book is a collection of problems previously published in the London Evening Standard newspaper. This is problem XXVI "A Magic Oblong" on page 26 of Part 1. The ranks add to 132 and the files to 66.
01 10 11 29 28 19 18 16 09 02 30 12 20 27 07 25 24 31 03 21 13 06 26 08 32 23 22 04 05 14 15 17
In a tour of step-sidestep type the first type of move, the step, is the main type of move used. The sidestep move is interpolated whenever the next main step would take the touring piece to an already visited cell. The method is effective in generating magic tours on any square boards of an odd number of cells, and various combinations of generative steps can be used.
On a torus of side n the coordinates of the moves should be kept less than n/2 units (a unit being the length of a wazir move, i.e. the distance from centre to centre of two adjacent cells), this is because a move of n units takes the piece all round the board and back to its initial cell. Thus a move of length k is equivalent to a move of length n - k in the opposite direction. For example on the 3×3 board a (0, 1) wazir move to the right is equivalent to a (0, -2) dabbaba move to the left, and a (1, 1) fers move up to the right is equivalent to a (-2, -2) alfil move in the opposite direction, or to a (1, -2) knight move steeply down to the right, or a (-2, 1) knight move shallowly up to the left!
Magic tours of the step-sidestep form can always be made diagonally magic by 'rotating' the torus (more accurately, circularly permuting the ranks or files) to bring the middle number (the average, A) to the centre cell, since the other numbers on the diagonals are then, because of the symmetry of the path, complementary pairs (adding to 2A).
The 3×3 diagonally magic square uses three types of move {0, 1}, {1, 1} and {1, 2} within the boundaries of the square. However, if we think of the board as having its top and bottom edges joined (to make a tube) and the left and right edges (the ends of the tube) joined to make a torus, these moves can be interpreted differently. The simplest way is to interpret them as a series of diagonal {1, 1} steps interrupted by {0, 1} steps. Under this interpretation the 3×3 magic square is an example of a step-sidestep tour. The fact that the ranks and files are magic in this type of tour is related to the fact that in a natural numbering of a square the diagonals, formed of {1, 1} moves, are particular examples of satins.
On the 5×5 board there are 24 distinct magic tours of this step-sidestep type. (Where ‘distinct’ means that we do not count rotations and reflections of the magic square as different.) Here are diagrams of them all, oriented acording to the Frénicle rule (smallest numbers in the first two cells at top left) and with the middle number, 13, in the centre cell. The magic sum is 5×13 = 65.
Wazir + Fers (King) 9 2 25 18 11 3 21 19 12 10 22 20 13 6 4 16 14 7 5 23 15 8 1 24 17 |
Fers + Dabbaba 3 16 9 22 15 20 8 21 14 2 7 25 13 1 19 24 12 5 18 6 11 4 17 10 23 |
Fers + Dabbaba 4 17 10 23 11 18 6 24 12 5 7 25 13 1 19 21 14 2 20 8 15 3 16 9 22 |
Fers + Alfil 7 3 24 20 11 4 25 16 12 8 21 17 13 9 5 18 14 10 1 22 15 6 2 23 19 |
Fers + Alfil 1 18 10 22 14 20 7 24 11 3 9 21 13 5 17 23 15 2 19 6 12 4 16 8 25 |
Wazir + Alfil 6 3 25 17 14 5 22 19 11 8 24 16 13 10 2 18 15 7 4 21 12 9 1 23 20 |
Wazir + Alfil 8 2 21 20 14 4 23 17 11 10 25 19 13 7 1 16 15 9 3 22 12 6 5 24 18 |
Dabbaba + Alfil 5 16 7 23 14 18 9 25 11 2 6 22 13 4 20 24 15 1 17 8 12 3 19 10 21 |
Wazir + Knight 3 14 25 6 17 22 8 19 5 11 16 2 13 24 10 15 21 7 18 4 9 20 1 12 23 |
Wazir + Knight 2 11 25 9 18 21 10 19 3 12 20 4 13 22 6 14 23 7 16 5 8 17 1 15 24 |
Wazir + Knight 4 12 25 8 16 23 6 19 2 15 17 5 13 21 9 11 24 7 20 3 10 18 1 14 22 |
Dabbaba + Knight 3 15 22 9 16 21 8 20 2 14 19 1 13 25 7 12 24 6 18 5 10 17 4 11 23 |
Dabbaba + Knight 2 14 21 8 20 23 10 17 4 11 19 1 13 25 7 15 22 9 16 3 6 18 5 12 24 |
Dabbaba + Knight 5 12 24 6 18 22 9 16 3 15 19 1 13 25 7 11 23 10 17 4 8 20 2 14 21 |
Fers + Knight 1 14 22 10 18 24 7 20 3 11 17 5 13 21 9 15 23 6 19 2 8 16 4 12 25 |
Fers + Knight 1 15 24 8 17 23 7 16 5 14 20 4 13 22 6 12 21 10 19 3 9 18 2 11 25 |
Fers + Knight 2 18 9 25 11 19 10 21 12 3 6 22 13 4 20 23 14 5 16 7 15 1 17 8 24 |
Fers + Knight 8 1 24 17 15 5 23 16 14 7 22 20 13 6 4 19 12 10 3 21 11 9 2 25 18 |
Alfil + Knight 3 12 21 10 19 24 8 17 1 15 20 4 13 22 6 11 25 9 18 2 7 16 5 14 23 |
Alfil + Knight 5 11 22 8 19 23 9 20 1 12 16 2 13 24 10 14 25 6 17 3 7 18 4 15 21 |
Alfil + Knight 3 17 6 25 14 19 8 22 11 5 10 24 13 2 16 21 15 4 18 7 12 1 20 9 23 |
Alfil + Knight 10 1 22 18 14 3 24 20 11 7 21 17 13 9 5 19 15 6 2 23 12 8 4 25 16 |
Knight 3 11 24 7 20 25 8 16 4 12 17 5 13 21 9 14 22 10 18 1 6 19 2 15 23 |
Knight 4 15 21 7 18 25 6 17 3 14 16 2 13 24 10 12 23 9 20 1 8 19 5 11 22 |
The first eight use only lateral and diagonal moves. The others all use knight moves for one of the steps, while in the last two both the steps are knight moves, so these two are magic knight tours of the torus. These two tours are given in W. S. Andrews Magic Squares and Cubes 1917 (Figures 19 and 20, page 11).
After entering the first 5 numbers, say in the (1, 2) direction, then there is a choice of directions for the knight sidestep. This cannot be forwards (1, 2) or backwards (−1, −2) since these lead to cells already used, also they cannot be the other ‘vertical’ moves (−1, 2), (1, −2) since the first of these does not alter the file and the second does not alter the rank on which the next sequence of (1, 2) moves begins, so if the step is vertical the sidestep must be horizontal. This is a general rule, applicable to other leapers and larger boards. In the 5×5 case the two horizontal sidesteps at right angles to the step, that is (2, −1) and (−2, 1) are also blocked, since they lead to cells already used; however this is not a general rule.
There are considerably more such tours on the 7×7 board. Here are the 12 tours in which the step and sidestep are the same type of move. There are four by knight {1, 2}, four by camel {1, 3} and four by zebra {2, 3}. Given the orientation of the first step, say (a, b), the side step can be (b, a), (−b, a), (b, −a), (−b, −a) each of which gives a magic tour, whereas the sidesteps (a, −b) and (−a, b) each give a semimagic tour (that is only the ranks or the files have a uniform sum).
Two of the 7×7 knight tours are pandiagonal, that is all 14 diagonals (lines of cells connected by fers moves) add up to the magic constant. The others are semi-pandiagonal, that is 7 diagonals in one direction and one in the other direction) add to the magic constant. The magic sum is 7×25 = 175.
As for the 5×5 case above the tours are cycled so the middle number 25 comes to the centre, and are oriented by the Frénicle rule.
Knight 4 23 49 19 38 8 34 41 11 30 7 26 45 15 22 48 18 37 14 33 3 10 29 6 25 44 21 40 47 17 36 13 32 2 28 35 5 24 43 20 39 9 16 42 12 31 1 27 46 |
Knight 10 5 49 37 32 27 15 41 29 24 19 14 2 46 16 11 6 43 38 33 28 47 42 30 25 20 8 3 22 17 12 7 44 39 34 4 48 36 31 26 21 9 35 23 18 13 1 45 40 |
Knight 8 4 49 38 34 23 19 41 30 26 15 11 7 45 18 14 3 48 37 33 22 44 40 29 25 21 10 6 28 17 13 2 47 36 32 5 43 39 35 24 20 9 31 27 16 12 1 46 42 |
Knight 5 27 49 15 37 10 32 41 14 29 2 24 46 19 28 43 16 38 11 33 6 8 30 3 25 47 20 42 44 17 39 12 34 7 22 31 4 26 48 21 36 9 18 40 13 35 1 23 45 |
Camel 11 6 43 38 33 28 16 37 32 27 15 10 5 49 21 9 4 48 36 31 26 47 42 30 25 20 8 3 24 19 14 2 46 41 29 1 45 40 35 23 18 13 34 22 17 12 7 44 39 |
Camel 6 16 33 43 11 28 38 49 10 27 37 5 15 32 36 4 21 31 48 9 26 30 47 8 25 42 3 20 24 41 2 19 29 46 14 18 35 45 13 23 40 1 12 22 39 7 17 34 44 |
Camel 3 18 33 48 14 22 37 49 8 23 38 4 19 34 39 5 20 35 43 9 24 29 44 10 25 40 6 21 26 41 7 15 30 45 11 16 31 46 12 27 42 1 13 28 36 2 17 32 47 |
Camel 14 3 48 37 33 22 18 38 34 23 19 8 4 49 20 9 5 43 39 35 24 44 40 29 25 21 10 6 26 15 11 7 45 41 30 1 46 42 31 27 16 12 32 28 17 13 2 47 36 |
Zebra 4 21 31 48 9 26 36 43 11 28 38 6 16 33 40 1 18 35 45 13 23 30 47 8 25 42 3 20 27 37 5 15 32 49 10 17 34 44 12 22 39 7 14 24 41 2 19 29 46 |
Zebra 7 26 45 15 41 11 30 36 13 32 2 28 47 17 23 49 19 38 8 34 4 10 29 6 25 44 21 40 46 16 42 12 31 1 27 33 3 22 48 18 37 14 20 39 9 35 5 24 43 |
Zebra 2 24 46 19 41 14 29 39 12 34 7 22 44 17 27 49 15 37 10 32 5 8 30 3 25 47 20 42 45 18 40 13 35 1 23 33 6 28 43 16 38 11 21 35 9 31 4 26 48 |
Zebra 5 20 35 43 9 24 39 48 14 22 37 3 18 33 42 1 16 31 46 12 27 29 44 10 25 40 6 21 23 38 4 19 34 49 8 17 32 47 13 28 36 2 11 26 41 7 15 30 45 |
The geometry of ‘straight lines’ on the torus is distinctly non-euclidean. A diagram can be drawn showing three straight lines formed by knight moves (2, 1), camel moves (−1, 3) and zebra moves (3, −2) starting at any cell and going in three completely different drections, and yet the three lines pass through the same seven ‘points’ (cell centres), each in a different order!
No step-sidestep magic knight tours are possible on the 9×9 board, since the primality conditions are not met.
Four magic knight torus tours are again possible on the 11×11 board as shown here.
Knight 6 46 97 16 56 107 26 77 117 36 87 98 17 57 108 27 67 118 37 88 7 47 58 109 28 68 119 38 78 8 48 99 18 29 69 120 39 79 9 49 89 19 59 110 121 40 80 10 50 90 20 60 100 30 70 81 11 51 91 21 61 101 31 71 111 41 52 92 22 62 102 32 72 112 42 82 1 12 63 103 33 73 13 43 83 2 53 93 104 23 74 114 44 84 3 54 94 13 64 75 115 34 85 4 55 95 14 65 105 24 35 86 5 45 96 15 66 106 25 76 116 |
Knight 7 52 97 21 66 100 24 69 114 38 83 96 20 65 110 23 68 113 37 82 6 51 64 109 33 67 112 36 81 5 50 95 19 32 77 111 35 80 4 49 94 18 63 108 121 34 79 3 48 93 17 62 107 31 76 78 2 47 92 16 61 106 30 75 120 44 46 91 15 60 105 29 74 119 43 88 1 14 59 104 28 73 118 42 87 11 45 90 103 27 72 117 41 86 10 55 89 13 58 71 116 40 85 9 54 99 12 57 102 26 39 84 8 53 98 22 56 101 25 70 115 |
Knight 24 7 100 83 66 38 21 114 97 69 52 110 82 65 37 20 113 96 68 51 23 6 64 36 19 112 95 67 50 33 5 109 81 18 111 94 77 49 32 4 108 80 63 35 93 76 48 31 3 107 79 62 34 17 121 47 30 2 106 78 61 44 16 120 92 75 1 105 88 60 43 15 119 91 74 46 29 87 59 42 14 118 90 73 45 28 11 104 41 13 117 89 72 55 27 10 103 86 58 116 99 71 54 26 9 102 85 57 40 12 70 53 25 8 101 84 56 39 22 115 98 |
Knight 26 6 107 87 56 36 16 117 97 77 46 108 88 57 37 17 118 98 67 47 27 7 58 38 18 119 99 68 48 28 8 109 78 19 120 89 69 49 29 9 110 79 59 39 90 70 50 30 10 100 80 60 40 20 121 51 31 11 101 81 61 41 21 111 91 71 1 102 82 62 42 22 112 92 72 52 32 83 63 43 12 113 93 73 53 33 2 103 44 13 114 94 74 54 23 3 104 84 64 115 95 75 55 24 4 105 85 65 34 14 76 45 25 5 106 86 66 35 15 116 96 |
Diagrams of many of the above tours are shown in the PDF on Augmented Knights and Leapers, classified according to the number of different move-types used when the board is considered to be a normal square instead of a torus. However the results were not enlightening. The interested reader is referred to the PDF #10.
A generalisation of this method, in which the numbers are entered on the lines in non-numerical order, is described by W. H. Benson and O. Jacoby in New Recreations with Magic Squares (1976) under the title of ‘New Cyclical Method’. However, I believe the basic idea goes back to C. Planck The Theory of Path Nasiks (1905) and probably to A. H. Frost Quarterly Journal of Mathematics (1878).
éBack to top