ç Knight's Tour Notes Index
Empress Tours: Knight + Rook
As noted in the Emperor page considerable new work has been reported by Yann Denef (France) in enumerating
11194 magic "two-knight tours" on the 8×8 board in which the link 32-33, between cells of opposite colour, can be any move type.
Among these besides 3560 Emperor tours are 2826 in which the connection is a {0,3} move, 1887 with a {0,5} move and 1667 with a {0,7} move,
all of which are Empress tours. Some of these will be the same as the 19th century French examples reported below.
The reader can explore the many diagrams on Yann's web pages:
http://ydenef.free.fr/english/2-kt.htm.
Sections on this page:
— Introduction
— Alternating Knight and Rook Moves
— Two-Move Empress Tours
— Three-Move Empress Tours
— Four-Move Empress Tours
é Introduction
A piece that can move either as knight or rook is known as an Empress, so long as it makes at least one knight move and at least one
rook mve longer than one step. Emperor tours, combining Knight and Wazir (i.e. single-step rook) now have their own page.
Tours by either of these pieces can be termed Imperial.
A class of imperial tours that has received intensive study on the 8×8 board are those that use only a small number of rook moves,
connected by chains of knight moves all of the same number of moves. In particular magic tours are easily constructed with two or four rook moves,
all the others being knight moves. These are also known, perhaps misleadingly, as "Two-Knight Tours" and "Four-Knight Tours".
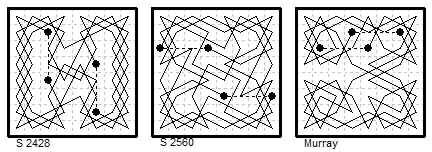
Results of this type were collected by H. J. R. Murray and are included in his manuscripts (1942 chapter XIV) and (1951 chapter X).
This was my main source for the first version of this article. He wrote that: "The problem was popular with French composers between 1880 and 1914
when nearly 300 two-chain magic tours were published in the Paris chess columns." It seems he was unaware of earlier work by "E.H." published as
articles on "Knightly Peripatetics" in the Glasgow Weekly Herald from 1873 onwards. I was able to consult the 1873-4 volume at the
British Library Newspaper depository when it was at Colindale [on 25 October 1996] and include some results of this, but further work needs to be
done in checking this source. Subsequently, through online research, I have located many of the original sources of these tours, mainly in the
puzzle column in Le Siècle run by M. A. Feisthamel, where they are presented as cryptotours.
In our tabular diagrams of these tours (which are retained from an earlier version of this page) the coloured cells highlight the eight numbers
1, 16, 17, 32, 33, 48, 49, 64 that mark the ends of the four quarters of the tour. In two-knight tours the links 16-17 and 48-49 are knight moves.
To assist in recognition of tours, the conventions are observed that we number the tour in such a way that the 32-33 move is as short as possible,
that the principal diagonal consists of even numbers, and the cell numbered 01 is on the left side of the board. (This has meant many changes from
the arrangements shown in the source articles.)
Tours of these types are also shown in the Emperor (Knight + Wazir) section. Some 8×8 magic Emperor tours have their end-pomnts, 1 and 64,
a {0,1} wazir-move apart, while others hav the rook moves {0,3}, {0,5} or {0,7} as the closure move 64-1. Since the cyclic renumbering of these
magic tours (making 1-64 become 32-33) are also magic, these can also be regarded as Empress tours. But they are excluded from the present section.
It is of course possible to construct Two-Knight and Four-Knight tours that are not imperial tours, since moves other than rook moves may connect
the ends of the knight paths. The connecting moves can, indeed, themselves be knight moves: this is the case in two of the magic tours by Jaenisch,
which he described as 'doubly reentrant' since 1 linked with 32 as well as 64, and 33 linked with 64 as well as 32.
é Alternating Knight and Rook Moves
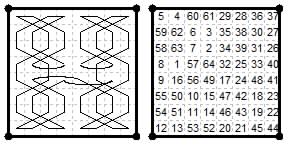
In the first online issue of The Games and Puzzles Journal #19 published in 2001 I wrote: The following note was sent by Professor Donald E. Knuth
of Stanford University (dated 16 Sep 2000): "I ran across a curious thing in The Strand Magazine volume 36 (1908), contributed by "Mr J.Wallis,
51, Holsworthy Square, Gray's Inn Road, W.C.": He constructed a tour of the chessboard in which knight's moves alternate with rook moves, and the square
is also magic [i.e. adds to the same sum, 260, in each rank, each file and the two main diagonals]. This was on page 480 of the American edition,
probably in the same place of the London edition since each number had 120 pages that year. ... So I have two questions: (1) Have you ever heard of this
"J.Wallis" before? (2) Have you ever heard of such alternating tours before? [Wallis also presented one for knight and bishop, but not magic, on page 360.]"
| 12 | 55 | 54 | 9 | 8 | 59 | 58 | 5 |
| 53 | 10 | 11 | 56 | 57 | 6 | 7 | 60 |
| 13 | 50 | 51 | 16 | 1 | 62 | 63 | 4 |
| 52 | 15 | 14 | 49 | 64 | 3 | 2 | 61 |
| 20 | 47 | 46 | 17 | 32 | 35 | 34 | 29 |
| 45 | 18 | 19 | 48 | 33 | 30 | 31 | 36 |
| 21 | 42 | 43 | 24 | 25 | 38 | 39 | 28 |
| 44 | 23 | 22 | 41 | 40 | 27 | 26 | 37 |
| 
|
| 12 | 54 | 55 | 9 | 8 | 58 | 59 | 5 |
| 13 | 51 | 50 | 16 | 1 | 63 | 62 | 4 |
| 53 | 11 | 10 | 56 | 57 | 7 | 6 | 60 |
| 52 | 14 | 15 | 49 | 64 | 2 | 3 | 61 |
| 20 | 46 | 47 | 17 | 32 | 34 | 35 | 29 |
| 21 | 43 | 42 | 24 | 25 | 39 | 38 | 28 |
| 45 | 19 | 18 | 48 | 33 | 31 | 30 | 36 |
| 44 | 22 | 23 | 41 | 40 | 26 | 27 | 37 |
|
In my response I wrote with an account of other alternating tours dating back to As-Suli (see the page on Princely Tours). I was unable to
find out any more about J. Wallis. but noted that by simple transformations Wallis's tour can be converted into other alternating tours similarly magic,
including this Empress tour, formed by interchanging the 2-3 and 6-7 ranks and files. (For the other two see the section on Queen tours). Some moves have
to be shown by curved lines for clarity. These tours are diagonally magic.
é Two-Move Empress Tours
{1,2} + {0,2} Empress = Templar
This augmented knight is the simplest piece in the Imperial (Rook + Knight) group, if one excludes the Emperor (Wazir + Knight).
The name is a companiaon to the Hospitaller (Knight + Alfil) which will be found in the Princely Tours sectio.
4×4 Board. Some tours with this pair of moves, showing various different symmetries were constructed
by R. J. French, E. Huber-Stockar, S. H. Hall and others in Fairy Chess Review 1941 (¶4772, ¶4842, ¶4892, ¶5042).
Other solvers contributed 17 further tours that were not diagrammed.
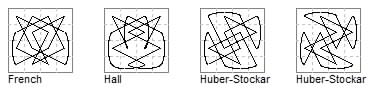
{1,2} + {0,3} Empress
4×4 Board. Some tours with these pairs of moves, showing various different types of symmetry were constructed
by R. J. French and E. Huber-Stockar in Fairy Chess Review 1941.

Magic tours 4×4 (nondiagonal) are possible with biaxial symmetry when the two end-points of the path are joined up
to give a closed path (Jelliss Chessics #26 1986).

The black dots mark 1, 8, 9, 16 The first two diagrams show the same closed tour numbered from different points;
such a magic tour is termed cyclic.
John Beasley (Variant Chess #64 2010 p.233) notes that the {0,3}{1,2} piece on the 4×4 board has four moves at each cell,
and that the tours above are self-complementary in the sense that when rotated a quarter turn they use the other two moves at each cell.
He also notes that they have the alternative magic sums 32 and 36 in all the odd and even diagonals, including the broken diagonals.
4×6 Board. More {0,3}{1,2} biaxial magic tours (Jelliss 10 Aug 1991) 50 in files 75 in ranks.
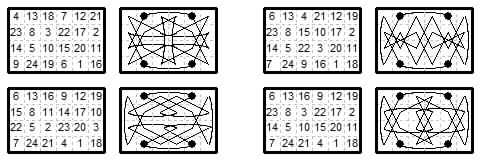
Four with origin in the outer ranks, Six with origin in the inner ranks.
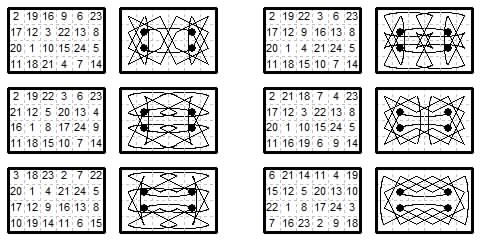
The arithmetical forms are shown since where curved {0,3} moves cross may be unclear.
8×8 Board.
There are seven magic knight tours with {0,3} link between end-points. In our catalogue (PDF #9) they are (03a) to (03g).
Five were found by Ligondès 1883/4, one by Murray 1940 and one by Marlow 1988.
Magic two-knight tours with {0,3} links.
(1) Le Siècle ¶1984 (2 Mar 1883) by Palamède (Ligondes). Asymmetric,
diagonals 352 & 216 from b4=1, or 344 & 224 from g1=1.
(2) Le Siècle ¶2386 (20 Jun 1884) by Palamède. Rotary, diagonals 312 and 256 from b4=1.
(3) Le Siècle ¶2392 (27 Jun 1884) by Adsum (Bouvier). Rotary, diagonals 232 and 256 from d5=1.

(4) Le Siècle ¶2428 (8 Aug 1884) by 'M. A. D. à Rouvres'. Rotary, diagonals 224 and 232 from c7=1.
(5) Le Siècle ¶2560 (9 Jan 1885) by Adsum (Bouvier). Rotary, diagonals 248 and 232 from a6=1.
(6) Example from Murray (1951) nearly axial, diagonals 208 and 312.
Here is a more attractive presentation of this tour. The diagram also shows the knight move links between quarters.
| 42 | 03 | 22 | 31 | 50 | 59 | 46 | 07 |
| 23 | 32 | 43 | 04 | 45 | 06 | 49 | 58 |
| 02 | 41 | 30 | 21 | 60 | 51 | 08 | 47 |
| 29 | 24 | 01 | 44 | 05 | 48 | 57 | 52 |
| 40 | 33 | 28 | 61 | 20 | 53 | 16 | 09 |
| 25 | 62 | 37 | 34 | 15 | 12 | 19 | 56 |
| 36 | 39 | 64 | 27 | 54 | 17 | 10 | 13 |
| 63 | 26 | 35 | 38 | 11 | 14 | 55 | 18 |
|

|
{1,2} + {0,5} Empress
8×8 Board
There are seven magic knight tours with end-points a {0,5} move apart (05a) to (05g) in the catalogue (in PDF 9).
Two by Bouvier 1876/82, one by Caldwell 1879, three by Francony 1881/2, and one by Ligondes 1883.
Magic two-knight tours with {0,5} links.
Here are eight magic tours of this type from the earlier years of the Feisthamel column.
(1) Le Siècle ¶850 (25 Jul 1879) rotary, diagonals 232 and 240.
(2) Le Siècle ¶940 (7 Nov 1879) rotary, diagonals 260±20.
(3) Le Siècle ¶2140b (7 Sep 1883) by Adsum (Bouvier). Axial, diagonally magic
(4) Le Siècle ¶2164c (5 Oct 1883) by Reuss. Axial, diagonals magic.

(5) Le Siècle ¶2398 (4 Jul 1884) by M. A. D. Rotary diagonals 216 and 256.
(6) Le Siècle ¶2404 (11 Jul 1884) by Reuss. Rotary, diagonals 280 and 204.
(7) Le Siècle ¶2416 (25 Jul 1884), rotary, diagonals 220 and 276.
(8) Le Siècle ¶2476 (3 Oct 1884) by Reuss. Rotary, diagonals 280 and 268.
{1,2} + {0,7} Empress
8×8 Board
There is just one magic knight tour with end-points a {0,7} move apart (07a).
It was one of the last found, by H. Mackay, J-C. Meyrignac and G. Stertenbrink in their computer search in 2003.
Magic two-knight tours with {0,7} links.
Here are some from Feisthamel's column in Le Siècle.
(1) ¶2032 (4 May 1883) asymmetric, diags 320 and 220.
(2) ¶2176 (19 Oct 1883) by Reuss. Axial, diags magic.
(3) ¶2464 (19 Sep 1884) by Adsum (Bouvier). Rotary, diagonals 280 and 264.
(4) ¶2512 (14 Nov 1884), rotary, diagonals 264 and 268.

(5) Le Siècle ¶2548 (26 Dec 1884) by Adsum (Bouvier). Rotary, diagonals 280 and 264.
(6)Le Siècle ¶3814 (1 Feb 1889), axial, diagonals 260±44. ??

é Three-Move Empress Tours
{1,2} + {0,1}{0,2} = Warden
This is the simplest three-pattern augmented knight in this class, with a newly proposed name, with moves WDN.
2×3 board. There is one tour using wazir, dabbaba and knight moves. It is rotary, crossing at the centre.

4×4 board. There are 8 WDN tours in the Frénicle list of 4×4 diagonally magic squares
but they have only four geometrical forms. The asymmetric tour can be numbered from either end (giving magic squares 231 + 424 in the list).
The three symmetric closed tours can be numbered from two different origins (giving 224 + 603 and 298 + 638 and 350 + 549 in the list).

8×8 board. Here are two four-knight magic tours from the Feisthamel column using wazir and dabbaba links.
(1) Le Siècle ¶1006 (23 Jan 1880), axial, diagonals 260±20.
(2) Le Siècle ¶1978 (2 Mar 1883), axial, diagonals 260.

The other diamagic tour above is the J. Wallis tour shown above in the Alternating moves section.
{1,2} + {0,1}{0,3}
2×4 board. The Wazir + Threeleaper + Knight piece gives a biaxial tour that is magic in ranks and files
when numbered about the long axis but only magic in the files when numbered about the short axis.
It is again a permute of the magic king tour.
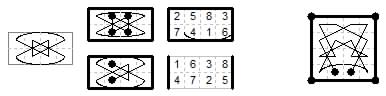
4×4 board. There is also a WTN tour among the Frénicle 4×4 diagonally magic squares (diagram above).
This is a closed version of the WN (Emperor) tour, the ends being joined and numbered from a new origin (It is 617 in the list of magic squares).
8×8 board. This was first published in "The Games and Puzzles Journal" #26 March-April 2003 together with the results
on rectangles given in the Emperor tour page. This connects d4-c4, d5-c5, c3-c6, d3-d6. The righthand side of this has the same geometrical form
as the Beverley tour, but not the same arithmetical form. (The numbers on the diagonals are the same as for a similar Emperor tour, but permuted.)
The diagonal sums are 240 and 280.
51 46 29 4 53 44 27 6
30 3 52 45 28 5 54 43
47 50 1 32 41 56 7 26
2 31 48 49 8 25 42 55
63 34 17 16 57 40 23 10
18 15 64 33 24 9 58 39
35 62 13 20 37 60 11 22
14 19 36 61 12 21 38 59
|

|
|
{1,2} + {0,1}{0,4}
8×8 Diagonally Magic Four-Knight 1-4 Empress Tours
These, of double half-board type, are by A. Béligne in Le Siècle
(1) ¶2308 (21 Mar 1884). (2) ¶3796 (11 Jan 1889).

{1,2} + {0,1}{0,7}
8×8 Magic Four-Knight 1/7 Empress Tour.
Reuss Le Siècle ¶3196 (4 Feb 1887).

Diagonally Magic Four-Knight 1/7 Empress Tours.
Eight examples from Le Siècle:
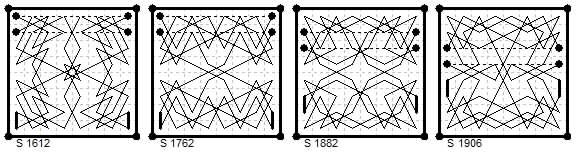
(1) ¶1612 (30 Dec 1881) by Béligne
(2) ¶1762 (23 Jun 1882) by L. de Croze,
(3) ¶1882 (10 Nov 1882) by M. A. F. (i.e. Feisthamel),
(4) ¶1906 (8 Dec 1882) by Béligne.

(5) ¶1930 (5 Jan 1883) by Béligne,
(6) ¶1942 (19 Jan 1883)
(7) ¶2230 (21 Dec 1883) by Adsum (Bouvier),
(8) ¶3208 (18 Feb 1887) by E. Grossetaite.
{1,2} + {0,2}{0,3}
8×8 board. Diamagic tours Le Siècle ¶2206 (23 Nov 1883) axial by R. Bricard
and ¶5212 (10 Feb 1893) asymmetric by M. A. F.
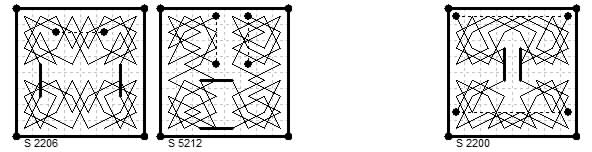
{1,2}+{0,2}{07}
Shown on the right above, Le Siècle ¶2200 (16 Nov 1883) by M. A. F. (Feisthamel).
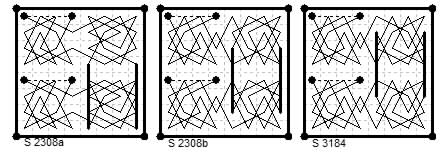
{1,2} + {0,3}{0,4}
8×8 board. Three diagonally magic tours by A. Béligne from Le Siècle:
¶2308a and b (21 Mar 1884) ¶3184 (21 Jan 1887).
Two reflected in the a8-h1 and the a1-h8 diagonals for comparison with the third.
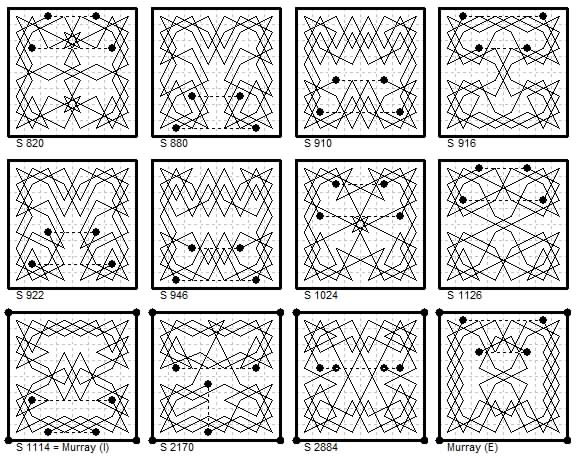
{1,2} + {0,3}{0,5}
8×8. Eight Magic and Four Diamagic Two-Knight 3-5 Empress Tours.
The two that were I and E in H. J. R. Murray's account are also shown in numerical form alongside,
though differently oriented from the geometrical diagrams.
|
TOUR I
| 02 | 35 | 32 | 61 | 04 | 33 | 30 | 63 |
| 57 | 60 | 03 | 34 | 31 | 62 | 05 | 08 |
| 36 | 01 | 58 | 11 | 54 | 07 | 64 | 29 |
| 59 | 56 | 37 | 26 | 39 | 28 | 09 | 06 |
| 22 | 25 | 12 | 55 | 10 | 53 | 40 | 43 |
| 13 | 48 | 23 | 38 | 27 | 42 | 17 | 52 |
| 24 | 21 | 46 | 15 | 50 | 19 | 44 | 41 |
| 47 | 14 | 49 | 20 | 45 | 16 | 51 | 18 |
|
TOUR E
| 38 | 61 | 18 | 09 | 40 | 63 | 20 | 11 |
| 17 | 08 | 39 | 62 | 19 | 10 | 41 | 64 |
| 60 | 37 | 16 | 51 | 30 | 33 | 12 | 21 |
| 07 | 50 | 59 | 36 | 13 | 22 | 31 | 42 |
| 58 | 15 | 06 | 29 | 52 | 43 | 34 | 23 |
| 05 | 28 | 49 | 14 | 35 | 32 | 53 | 44 |
| 48 | 57 | 26 | 03 | 46 | 55 | 24 | 01 |
| 27 | 04 | 47 | 56 | 25 | 02 | 45 | 54 |
|
From Le Siècle
(1) ¶820 (20 Jun 1879) 260±24 with two complete octangles.
(2) by Béligne ¶880 (29 Aug 1879) 260±4.
(3) ¶910 (3 Oct 1879) 260±54
(4) ¶916 (10 Oct 1879) 260±20.
(5) by Béligne ¶?22 (17 Oct 1879) 260±4.
(6) by Béligne ¶946 (14 Nov 1879) 260±54.
(7) ¶1024 (13 Feb 1880) 260±4.
(8) ¶1126 (11 Jun 1880) 260±28.
(9) Le Siècle ¶1114 (28 May 1880) = Murray tour I.
(10) by Reuss Le Siècle ¶2170 (12 Oct 1883) asymmetric, near axial.
(11) by de Hijo Le Siècle ¶2884 (29 Jan 1886). The two rook moves overlap.
(12) This is E in Murray's list.
{1,2} + {0,3}{0,7}
8×8 Twelve Magic (nondiagonal) Two-Knight 3-7 Empress Tours.
Here we show alternative presentations of the first four examples below. The first, derived from Vandermonde's method of constructing knights' tours
from pseudotours. These are given in Murray's account of the subject where he writes: "[the method] serves with little modification for the
construction of two-chain magic tours on the chessboard. Indeed, if Vandermonde had used an arithmetical notation instead of a geometrical diagram,
and had happened to adopt the right cell for his starting point, his two-knights' tour would have been magic." (The diagonals add to 248 and 272).
The diagonals in the second tour are 192 and 328 (i.e. 260 plus or minus 68).
VANDERMONDE TOUR
| 34 | 37 | 64 | 23 | 58 | 17 | 12 | 15 |
| 63 | 24 | 35 | 38 | 11 | 14 | 57 | 18 |
| 36 | 33 | 22 | 61 | 20 | 59 | 16 | 13 |
| 25 | 62 | 39 | 44 | 05 | 10 | 19 | 56 |
| 40 | 03 | 26 | 21 | 60 | 55 | 46 | 09 |
| 29 | 32 | 43 | 04 | 45 | 06 | 49 | 52 |
| 02 | 41 | 30 | 27 | 54 | 51 | 08 | 47 |
| 31 | 28 | 01 | 42 | 07 | 48 | 53 | 50 |
|

|
MURRAY TOUR
| 06 | 31 | 02 | 55 | 10 | 63 | 34 | 59 |
| 01 | 54 | 07 | 62 | 03 | 58 | 11 | 64 |
| 30 | 05 | 32 | 09 | 56 | 33 | 60 | 35 |
| 53 | 08 | 29 | 04 | 61 | 36 | 57 | 12 |
| 28 | 41 | 52 | 45 | 20 | 13 | 24 | 37 |
| 51 | 44 | 49 | 40 | 25 | 16 | 21 | 14 |
| 48 | 27 | 42 | 19 | 46 | 23 | 38 | 17 |
| 43 | 50 | 47 | 26 | 39 | 18 | 15 | 22 |
|

|
The other two examples are from the "Knightly Peripatetics" in the Glasgow Weekly Herald 1873-4.
The tours were set as problems, and the solution was published a week or two later, hence the two dates.
Geometrical diagrams are omitted. The first is X June 14 - 21, 1873 (diagonals 288, 232).
The second is XVI Sept 20 - Oct 4, 1873 (diagonals 356, 164).
TOUR X
| 54 | 51 | 42 | 03 | 62 | 23 | 14 | 11 |
| 43 | 02 | 55 | 52 | 13 | 10 | 63 | 22 |
| 50 | 53 | 04 | 41 | 24 | 61 | 12 | 15 |
| 01 | 44 | 49 | 56 | 09 | 16 | 21 | 64 |
| 48 | 05 | 32 | 25 | 40 | 33 | 60 | 17 |
| 31 | 28 | 45 | 08 | 57 | 20 | 37 | 34 |
| 06 | 47 | 26 | 29 | 36 | 39 | 18 | 59 |
| 27 | 30 | 07 | 46 | 19 | 58 | 35 | 38 |
| |
TOUR XVI
| 64 | 43 | 08 | 53 | 28 | 41 | 06 | 17 |
| 09 | 30 | 63 | 42 | 07 | 18 | 51 | 40 |
| 44 | 33 | 54 | 29 | 52 | 27 | 16 | 05 |
| 31 | 10 | 45 | 62 | 19 | 04 | 39 | 50 |
| 34 | 55 | 20 | 03 | 46 | 61 | 26 | 15 |
| 21 | 32 | 11 | 36 | 13 | 38 | 49 | 60 |
| 56 | 35 | 02 | 23 | 58 | 47 | 14 | 25 |
| 01 | 22 | 57 | 12 | 37 | 24 | 59 | 48 |
|
|
(1) Derived from Vandermonde's circuit, diagonals 260±12.
(2) Murray example, diagonals 260±68.
(3) and (4) E. H. in Glasgow Weekly Herald ¶X (14 Jun 1873) diagonals 260±28.
and ¶XVI (20 Sep/4 Oct 1873) diagonals 260±96.
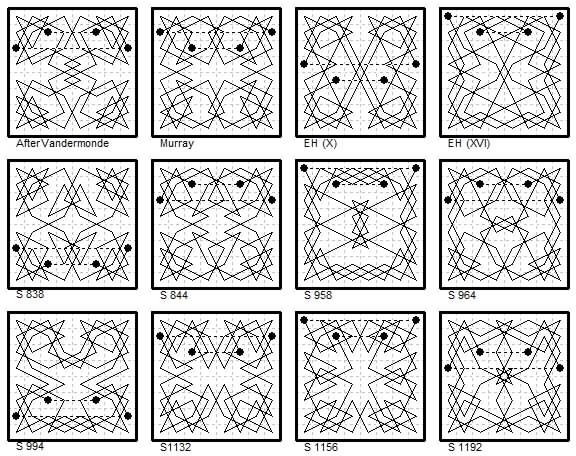
The 3-7 Empress seems to have generated the most magic tours in Le Siècle.
These are a sample.
(5) by Clerville ¶838 (11 Jul 1879) 260±56.
(6) by Celina (Francony) ¶844 (18 Jul 1879) 260±132.
(7) ¶958 (28 Nov 1879) 260±28.
(8) ¶964 (5 Dec 1879) 260±28.
(9) ¶994 (9 Jan 1880) 260±56.
(10) ¶1132 (18 Jun 1880) 260±148.
(11) para;1156 (17 Jul 1880) 260±76.
(12) ¶1192 (27 Aug 1880) 260±136.
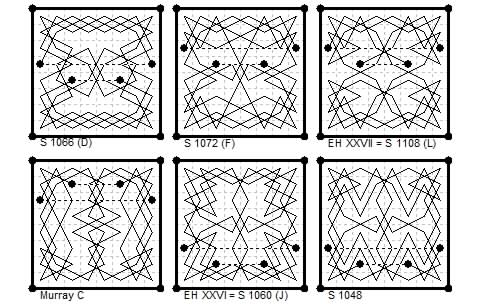
8×8 Six Diamagic Two-Knight 3-7 Empress Tours.
Five of these are D, F, L, C and J in Murray's list (1951).
TOUR C
| 34 | 21 | 64 | 13 | 36 | 17 | 60 | 15 |
| 63 | 12 | 35 | 20 | 61 | 14 | 37 | 18 |
| 22 | 33 | 62 | 09 | 40 | 19 | 16 | 59 |
| 11 | 42 | 55 | 24 | 57 | 26 | 07 | 38 |
| 54 | 23 | 10 | 41 | 08 | 39 | 58 | 27 |
| 43 | 32 | 03 | 56 | 25 | 46 | 49 | 06 |
| 02 | 53 | 30 | 45 | 04 | 51 | 28 | 47 |
| 31 | 44 | 01 | 52 | 29 | 48 | 05 | 50 |
|
TOUR D
| 60 | 51 | 12 | 03 | 62 | 53 | 14 | 05 |
| 11 | 02 | 61 | 52 | 13 | 04 | 63 | 54 |
| 50 | 59 | 10 | 41 | 24 | 55 | 06 | 15 |
| 01 | 40 | 49 | 58 | 07 | 16 | 25 | 64 |
| 48 | 09 | 32 | 23 | 42 | 33 | 56 | 17 |
| 31 | 22 | 39 | 08 | 57 | 26 | 43 | 34 |
| 38 | 47 | 20 | 29 | 36 | 45 | 18 | 27 |
| 21 | 30 | 37 | 46 | 19 | 28 | 35 | 44 |
|
TOUR F
| 38 | 47 | 40 | 29 | 36 | 25 | 18 | 27 |
| 21 | 30 | 37 | 46 | 19 | 28 | 35 | 44 |
| 48 | 39 | 20 | 41 | 24 | 45 | 26 | 17 |
| 31 | 22 | 49 | 58 | 07 | 16 | 43 | 34 |
| 50 | 59 | 32 | 23 | 42 | 33 | 06 | 15 |
| 01 | 10 | 61 | 08 | 57 | 04 | 55 | 64 |
| 60 | 51 | 12 | 03 | 62 | 53 | 14 | 05 |
| 11 | 02 | 09 | 52 | 13 | 56 | 63 | 54 |
|
TOUR J
| 34 | 57 | 64 | 13 | 36 | 17 | 24 | 15 |
| 11 | 62 | 35 | 58 | 23 | 14 | 19 | 38 |
| 56 | 33 | 12 | 63 | 18 | 37 | 16 | 25 |
| 61 | 10 | 05 | 22 | 59 | 44 | 39 | 20 |
| 04 | 55 | 60 | 43 | 06 | 21 | 26 | 45 |
| 09 | 32 | 53 | 02 | 47 | 28 | 49 | 40 |
| 54 | 03 | 30 | 07 | 42 | 51 | 46 | 27 |
| 31 | 08 | 01 | 52 | 29 | 48 | 41 | 50 |
|
TOUR L
| 12 | 47 | 14 | 55 | 10 | 51 | 18 | 53 |
| 59 | 56 | 11 | 46 | 19 | 54 | 09 | 06 |
| 48 | 13 | 58 | 15 | 50 | 07 | 52 | 17 |
| 57 | 60 | 49 | 20 | 45 | 16 | 05 | 08 |
| 24 | 21 | 32 | 61 | 04 | 33 | 44 | 41 |
| 01 | 36 | 23 | 34 | 31 | 42 | 29 | 64 |
| 22 | 25 | 38 | 03 | 62 | 27 | 40 | 43 |
| 37 | 02 | 35 | 26 | 39 | 30 | 63 | 28 |
|
However I have since found D in Le Siècle ¶1066 (2 Apr 1880)
and F ¶1072 (9 Apr 1880) by X a Belfort (Reuss).
And L ¶1108 (21 May 1880) and earlier in Glasgow Weekly Herald as ¶XXVII (1874 p.88).
Also J is in the E. H. column in Glasgow Weekly Herald as ¶XXVI (7/21 Feb 1874)
and in Le Siècle ¶1060 (26 Mar 1880).
The sixth is one I found when I made an attempt (c.1988) to check Murray's enumeration,
but have since found that it is also in Le Siècle ¶1048 (12 Mar 1880).
8×8 Three diamagic Two-Knight 3-7 Empress Tours. These are M, N and O in Murray's list.
N and M appear as by X a Belfort (Reuss) in Le Siècle ¶1084 (23 Apr 1880) and ¶1096 (7 May 1880).
Tour O which has only binary symmetry (when 1-32 and 33-64 are joined to make a pseudotour) is formed by combining the paths
used in the quaternary tours M and N, which cover the same set of cells.
The forward and reverse numberings of tour O are both shown since these numberings are very similar and can be easily confused.
This was pointed out to me in an email from Jaime Gutierrez Salazar in Dec 2016, who traces the tour back to General Parmentier (1890s).
In Rouse Ball (1939/1956 p.184) tour O is shown in the first numbering here (transposed) and is attributed to A. Rilly (1905).
The four numberings in M, N, and O and its reverse, differ only in the sequence of numbers round the four hexagons shown in the last diagram.
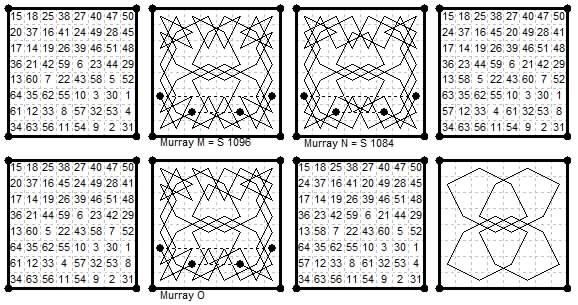
An alternative presentation of the tours
TOUR M
| 34 | 61 | 64 | 13 | 36 | 17 | 20 | 15 |
| 63 | 12 | 35 | 60 | 21 | 14 | 37 | 18 |
| 56 | 33 | 62 | 07 | 42 | 19 | 16 | 25 |
| 11 | 08 | 55 | 22 | 59 | 26 | 41 | 38 |
| 54 | 57 | 10 | 43 | 06 | 39 | 24 | 27 |
| 09 | 32 | 03 | 58 | 23 | 46 | 49 | 40 |
| 02 | 53 | 30 | 05 | 44 | 51 | 28 | 47 |
| 31 | 04 | 01 | 52 | 29 | 48 | 45 | 50 |
|
TOUR N
| 34 | 57 | 64 | 13 | 36 | 17 | 24 | 15 |
| 63 | 12 | 35 | 58 | 23 | 14 | 37 | 18 |
| 56 | 33 | 62 | 05 | 44 | 19 | 16 | 25 |
| 11 | 04 | 55 | 22 | 59 | 26 | 45 | 38 |
| 54 | 61 | 10 | 43 | 06 | 39 | 20 | 27 |
| 09 | 32 | 03 | 60 | 21 | 46 | 49 | 40 |
| 02 | 53 | 30 | 07 | 42 | 51 | 28 | 47 |
| 31 | 08 | 01 | 52 | 29 | 48 | 41 | 50 |
|
TOUR O
| 34 | 57 | 64 | 13 | 36 | 17 | 24 | 15 |
| 63 | 12 | 35 | 58 | 23 | 14 | 37 | 18 |
| 56 | 33 | 62 | 07 | 42 | 19 | 16 | 25 |
| 11 | 08 | 55 | 22 | 59 | 26 | 41 | 38 |
| 54 | 61 | 10 | 43 | 06 | 39 | 20 | 27 |
| 09 | 32 | 03 | 60 | 21 | 46 | 49 | 40 |
| 02 | 53 | 30 | 05 | 44 | 51 | 28 | 47 |
| 31 | 04 | 01 | 52 | 29 | 48 | 45 | 50 |
|
{1,2} + {0,4}{0,6}
Diamagic four knight tours Le Siècle ¶4862 (26 Feb 1892) by Adsum
and Le Siècle ¶5562 (26 Jan 1894) by Grossetaite.
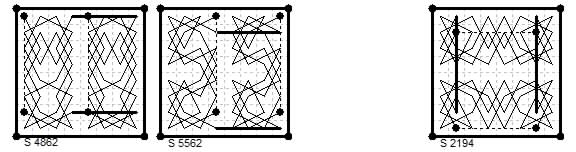
{1,2} + {0,5}{0,6}
Diamagic four knight tour from Le Siècle ¶2194 (9 Nov 1883) by Adsum. Above right.
{1,2} + {0,5}{0,7}
8×8 Magic Two-Knight 5-7 Empress Tours.

Here are some nondiagonally magic tours from Le Sècle.
(1) A. Béligne ¶832 (4 Jul 1879) 260±20.
(2) ¶970 (12 Dec 1879) 260±4.
(3) ¶1180 (13 Aug 1880) 260±40.
(4) ¶1204 (10 Sep 1880) 260±12.
(5) ¶1228 (8 Oct 1880) 260±88.
(6) ¶1414 (13 May 1881) 260±124.
(7) by Adsum ¶1468 (15 Jul 1881) 260±44.
(8) by L. de Croze ¶1492 (12 Aug 1881) 260±84.
é Four-Move Empress Tours
{1,2} + {0,1}{0,2}{0,3} Empress
8×8 board. This is the tour shown above in the Alternating moves section.
A Knight + three types of Rook move (Jelliss 2001). Derived from Wallis (1908), by interchange of the 2-3 and 6-7 ranks and files.
Also rotated 90 degrees to conform to the Frénicle convention.