Sections on this page: — King Tours — Alternating King Tours — Semi-Magic King Tours — Semi-Magic 6×6 King Tours — Magic King Tours
Since the king, a {0, 1} + {1, 1} mover, can make wazir moves, all wazir tours are also king tours. In retrospect king tours can be seen as the basis of various designs in Celtic Art taking the form of interlacing ribbons. Details of these are now shown on a separate page. The earliest examples of king tours on the chessboard that I have found appear as solutions to cryptotours in French newspapers of 1876-7. This led soon to construction of magic king tours on this board. These results anticipate the work of myself and Tom Marlow reported in The Games and Puzzles Journal in 1997. Mathematics of the enumeration of king tours began in Chess Amateur in 1908, where T. H. Neal published some results for king tours on two ranks of the chessboard, showing that the numbers were related to the Fibonacci sequence. T. R. Dawson enumerated king tours of the 3×3 board, open and closed, in British Chess Magazine, January 1949. The most recent work reported here [August 2022] is from Walter Trump (Nuremberg, Germany) who has enumerated semimagic king tours on 4×4 and 6×6 boards, and has shown that magic king tours are not possible on these smaller boards.
On the 2×n board (n > 2) the link between two adjacent files in a diagram of a king's closed tour is either a pair of lengthwise moves (=) or a pair of diagonal moves (×}; two choices in each of n − 1 cases, hence the total number of oriented tour diagrams is T(n) = 2^(n − 1). This formula breaks down for n = 2 since the board is then square and there is an extra diagram because the bow-tie shaped tour can be rotated to figure-of-eight shape.

All these tours are symmetrical about the horizontal axis. Under H(n) in the following table we count those that are symmetric about the vertical axis also (shown by heavier lines in the diagrams above). We have two choices at each pair of files in one half, and in the centre pair when n is even, so the number of these biaxial tours is H(n) = 2^h, where h is n/2 when n is even, and (n − 1)/2 when n is odd. The total T(n) is made up of 1 from each biaxial tour, 2 from each axial tour, so the number of geometrically distinct tours, for n > 2, is G = H + A/2 = H + (T − H)/2 = (T + H)/2 = 2^(n − 2) + 2^(h − 1).
Table of results:
n = 2 3 4 5 6 7 8 9 10 11 12
T = 3 4 8 16 32 64 128 256 512 1024 2048
h = 1 1 2 2 3 3 4 4 5 5 6
H = 2 2 4 4 8 8 16 16 32 32 64
A = 0 1 2 6 12 28 56 120 240 496 992
G = 2 3 6 10 20 36 72 136 272 528 1056
R = 3 8 22 48 116 256 584 1280 2832 6144 13344
The last line of the table above counts the number of geometrically distinct reentrant tours, that is open tours where the ends are a king move apart. Since each 2×n closed king tour is symmetric about the horizontal axis we can derive only n+1 geometrically distinct reentrant tours from an axial tour by deleting a move: n−1 from the (=) or (×) moves and 2 from the end moves, while from a biaxial tour we can derive h+1. So the number of geometrically distinct reentrant tours is R = (n+1)A + (h+1)H, though n=2 is again an exceptional case.
The following diagrams list all the geometrically different open tours for n = 1 to 4:

and the 2×5 open tours, in smaller scale, classified by separation of end points:

We now look at recursion relations and formulae to calculate the numbers of open tours for longer boards. An open king tour with both ends in the same file is only possible if the file is an end-file of the board and, since joining the ends produces a closed tour, the number of such tours on a board 2×n is the same as the number of closed tours, 2^(n−1).
Any 2×n open king tour with ends on files p and q (p < q) consists (except when p = 1 or q = n) of reentrant tours of the end sections (with both their terminals on the p and q files) joined by an end-to-end tour of the middle section (with terminals on the p+1 and q−1 files). The reentrant sections total 2^(p−1) and 2^(n−q), from the formula for closed tours.
To complete the enumeration we need to know the number L(n) of tour-diagrams on a 2×n board, with one end at the top of the first file and the other end in the last file. The sequence L(n) has the initial values L(1) = 1 and L(2) = 4 and obeys the recurrence relation L(n) = 2L(n−1) + 4 L(n−2), since the initial section can be either of the two forms (a) or (b), derived from a tour of length n−1, or any of the four forms (c), ..., (f), derived from a tour of length n−2.

It is possible to express L(n) in terms of the Fibonacci numbers as L(n) = 2^(n−1).F(n+1), where F(1) = F(2) = 1 and F(n) = F(n−1) + F(n−2), giving the familiar series 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ....
Half of these L-type diagrams end at the top right and half at the bottom right, but when counted geometrically it appears that the numbers are equal in the even cases but differ in the odd cases since the number of symmetric tours are different, e.g. in case 3 there are 6 diagrams in each class, but the first consists of 3 asymmetric tours, the second of 2 symmetric and 2 asymmetric (2×3 = 6 and 2 + 2×2 = 6); and in case 5 there are 64 diagrams in each class, 32 asymmetric in the first class, 8 symmetric plus 28 asymmetric in the second class (2×32 = 64 and 8 + 2×28 = 64).
The number of king open tours from a given corner of a 2×n board, K(n), follows the similar recurrence: K(1) = 1, K(2) = 6 and K(n) = 2^(n−1) + 2K(n−1) + 4K(n−2), since diagrams (a) to (f) still apply, the additional term being the number of reentrant tours with both ends in the initial file. From this recurrence we calculate K(3) = 20, K(4) = 72, K(5) = 240, agreeing with the totals found by construction. This is also solved in Fibonacci numbers as: K(n) = 2^n.F(n+1) − 2^(n−1), a formula given by T. H. Neal (1908).
We can now determine the number of geometrically distinct symmetric tours. For axial tours: the number with horizontal axis for n>2 is 2^(n−1) to which must be added K(n/2) + 2K((n−2)/2) with vertical axis when n is even. For rotary tours: 2K((n−1)/2) when n is odd, K(n/2) + 2K((n−2)/2) when n is even. So the total of symmetric tours is S = A + Z.
The open tours with one end at the top of the pth file (p not 1 or n) consist of either a reentrant tour of the files p to n, followed by a tour from a corner of the files p−1 to 1, or a reentrant tour of the files p to 1 and a tour from a corner of the files p+1 to n. Denoting the total by K(p,n) we have, from the above results: K(p,n) = 2^(n−p).2.K(p−1) + 2^(p−1).2.K(n−p), where the K-value is doubled since there are two possible links from the reentrant section to the other part. This simplifies, in another formula due to T. H. Neal (1908), to: K(p,n) = 2^n.[F(p) + F(n+1−p) − 1]. Of course K(1,n) = K(n,n) = K(n) and K(p,n) = K(n+1−p,n).
We can now calculate the total number of 2×n king open tours, T(n), by summing the K(1,n) from 1 to n, with the help of the Fibonacci property that the sum of F(m) over m from 1 to n is F(n+2) − 1. This gives T(n) = 2^n.[4F(n+1) − (n+3)]. The number of geometrically distinct tours can then be calculated for each n (>2) by G = (T + 2S)/4.
Table of results for open tours:
n = 1 2 3 4 5 6 7 8 9
F = 1 1 2 3 5 8 13 21 34
L = 1 4 12 40 128 416 1344 4352 14080
K = 1 6 20 72 240 800 2624 8576 27904
A = 0 2 4 16 16 64 64 240 256
Z = 0 1 2 8 12 32 40 112 144
S = 1 3 6 24 28 96 104 352 400
T = 1 12 48 208 768 2752 9472 32000 106496
G = 1 3 15 64 206 736 2420 8176 26824
Here F = Fibonacci numbers, L = Tour diagrams from given corner to board end, K = Tour diagrams from given corner, A = axial, Z = rotary, S = symmetric, T = Total of tour diagrams and G = geometrically distinct. The figures in the first five columns of the table have been enumerated by construction as above, the other figures have been calculated from the recursions or formulae, but have not been independently checked.
The 3×3 tours, open and closed, were enumerated by T. R. Dawson (1949). There are 2 closed tours 3×3; one polygonal, the other with one self-intersection.
On the 3×3 board Dawson reported 51 geometrically distinct open king tours (3 of wazir type), of which 4 are symmetric (1 of wazir type) and 18 are reentrant (1 of wazir type: the reentering move being a non-wazir move).
On the 3×4 board I find 37 closed king tours; 13 polygonal, 16 with one intersection, 7 with two intersections, and 1 with three intersections. Of these 14 are symmetric; 5 centrally and 9 (including the wazir tour) axially.
The closed 3×4 tours give rise to 366 reentrant open tours, so the full number of open tours is likely to be very large, but among these there are 40 with axial symmetry: 14 reentrant, derived from the seven axially symmetric closed tours, including the wazir case, that cross the axis twice at right angles. Of the 26 others, 23 differ from 4×4 closed tours only by omission of a straight base line, the 3 other cases are shown.

3×3. There are four centro-symmetric king open tours of the 3×3 board. They all have the property that the sums of their ranks and files form arithmetic progressions, i.e. sequences with a fixed common difference. I call tours with this numerical property arithmic (from arithmos meaning number).

The first has ranks and files adding to the same progression 9, 15, 21 (cd 6). The others have one progression in the rank sums and another in the file sums. The second has ranks 9, 15, 21 (cd 6) files 8, 15, 22 (cd 7). The third has ranks 7, 15, 23 (cd 8) files 14, 15, 16 (cd 1). The fourth has ranks 6, 15, 24 (cd 9) files 14, 15, 16 (cd 1). In all of them, because the symmetry places the middle number 5 in the middle cell and places pairs of complements adding to 10 in the diametrally opposite cells the lines through the central cell all add to 15. Transposing the figures 2 and 8 in the first tour gives us the familiar 3×3 magic square. To make the second and third king tours magic we cycle 1-2-9-8-1. To make the wazir tour magic requires more manipulation. I have found this type of process of transforming arithmic king tours effective in generating magic tours on various boards.
3×5 and 3×7 Boards. In the 3×5 and 3×7 arithmic king tours below the moves are completely regular, being diagonal except where they meet a board edge when the king takes a lateral step along the edge and then resumes its diagonal moves as if reflected from the edge. The ranks of the 3×5 add to the progression 39 40 41 and the files to 22 23 24 25 26 (both cd = 1), the middle numbers being the magic constants for rank and file. The ranks of the 3×7 add to 76 77 78 and the files to 30 31 32 33 34 35 36 successively. Arithmic king tours of this type seem to be possible on any odd-sided oblong where the sides have no common factor.

3×9 Board. An arithmic symmetric king tour, files 38 39 40 41 42 43 44 45 46 (cd 1), ranks 106 126 146 (cd 20). Not of the regular pattern.


See the section on Semi-magic King tours below for more on 4x4 boards.
Symmetric open semi-arithmic 5×5 king tour. The files add to 63 64 65 66 67 (cd 1), but the ranks are irregular, adding to 53 73 65 57 77.
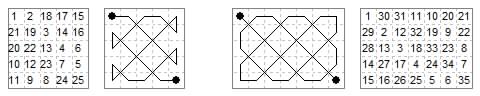
Arithmic 5×7 king tour is possible as for the 3×5 and 3×7 cases. The ranks add to the successive numbers 124 125 126 127 128 and files to 87 88 89 90 91 92 93.
An arithmic king tour is again possible. The ranks add to 205 206 207 208 209 and the files to 111 112 113 114 115 116 117 118 119 (207 and 115 being the magic constants).

On this board I have noted some semi-magic king tours of similar structure to the above arithmic tours. The files add to 111 (three pairs of complements adding to 37). The ranks of the first add to 118, 120, 110, 112, 102, 104, and of the second to 122, 124, 112, 110, 98, 100.
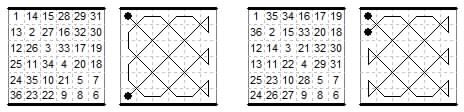
This diagram shows an arithmic King Tour in which the ranks sum to all the successive values from 285 to 291 and the files to the successive values from 220 to 228.
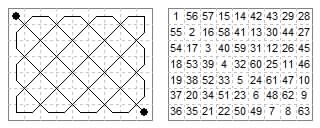
The middle rank and file are naturally magic, consisting of pairs of complements (adding to 64) plus the middle average number 32, giving the required totals of 288 and 224.
The earliest examples of 8×8 king tours I have found appear as solutions to cryptotours in French newspapers of 1876-7.
(1) Le Siecle problem 34 (15 Dec 1876) open.
(2) Le Gaulois problem 47 (29 May 1877) an irregular open tour by 'J. Faer'.
(3) Le Siecle problem 190 (8 Jun 1877) axial tour by M[onsieur] Clerville.
(4) Le Galois problem 68 (19 Jun 1877) an approximate biaxial tour by 'Mme Celina Fr' (Francony).
(5) problem 82 (4 Jul 1877) axial by 'Aristide Lejuste'.
(6) Le Siecle problem 232 (27 Jul 1877) biaxial by Clerville.
(7) problem 250 (17 Aug 1877) axial by A. Béligne.
(8) Le Gaulois problem 124 (17 Aug 1877) axial.
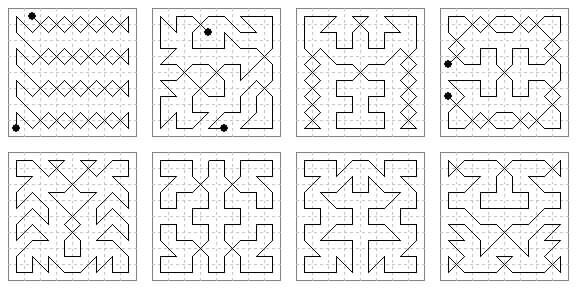
(9) Le Gaulois problem 145 (9 Sep 1877) axial open and
(10) problem 187 (24 Oct 1877) axial closed.
(11) Le Siecle problem 310 (26 Oct 1877) biaxial.
(12) Le Gaulois problem 208 (15 Nov 1877) axial open.
In the closed tours I have joined the end-points since their positions seem irrelevant.
Axial tours are semi-magic in the ranks if the end-points are symmetrically placed,
but this was not pointed out in the above problems.
Such tours are easy to construct so not detailed further here.
I published this in Jeepyjay Diary 12 October 2014. All numbers in sequence is apparently not possible.
With the condition 'minimum crossovers' it is probably unique. It includes a 6×6 solution.
The Kashmir poet Rudrata (c.900ad) gave an 'elephant' tour of a two-rank board in the form of a saw-tooth pattern of alternating wazir and fers moves, and as-Suli, working about the same time but in Baghdad, gave complete 8×8 tours of alternating moves of knight with fers and alfil but surprisingly, considering that the alternating wazir-fers tour is a type of king tour, no further example seems to have appeared until my quaternary example (found in the 1970s) was published in Chessics #18, 1984. Clive Grimstone, working independently sent me 20 examples on the 8×8 board at about the same time (30 April 1983), calling them 'ant' tours.
Theorem: A closed alternating king tour requires a board even by even, and the fers moves must form a fixed arrangement of crosses in the 2×2 blocks.
Proof: At the corner a1 the only fers move is a1-b2. At c1 the only fers move now available is c1-d2, since c1-b2 would give two successive fers moves. Similarly e1-f2 is forced. Continuing along the first rank we conclude that it must contain an even number of cells, since each fers move uses two files. A similar construction from the last cell back to a1 produces a pattern of n/2 crosses along the first two ranks. Now apply the same argument to the third rank. No fers moves are possible from rank 3 to rank 2 since all cells in rank 2 have fers moves assigned. So again we get the pattern of crosses. And the same for all other pairs of ranks.
There is one alternating king tour on any board 2×2.h and it has biaxial symmetry. On four-rank boards I find 1 tour 4×4, 3 tours 4×6, 6 tours 4×8. On the 6×6 board I find 5 solutions, all with diferent types of symmetry, including the first asymmetric example. I also have a note of 39 tours 6×8, not checked (4 biaxial, 9 with short axis, 3 with long axis, 4 centrosymmetric, and 19 asymmetric).
Observation: In closed tours, the moves along one pair of opposite edges must consist of fers-wazir-fers triangles. In the square diagrams below these are taken to be the vertical edges. This property is not true in open tours, as the examples show.

On the 8×8 there are over a hundred tours, but there are only 6 with biaxial symmetry. The first is the first one I found and published in Chessics (1984). The last three shown here were among those by Clive Grimstone.

A semi-magic tour has the ranks adding to the magic constant, but the files may vary.
Semimagic King tours are possible on any even-sided square boards, but not on odd-sided squares.
As noted above there are three geometrically distinct 2×2 open king tours (one being a wazir tour). Two of these, the axially symmetric ones, generate semimagic tours.
1 4 1 4 2 3 3 2
Walter Trump (Nuremberg Germany) has circulated a list [September 2022] of 1346 semimagic king tours on the 4×4 board.
They are arranged in column form in the attached PDF: Trump 4×4 PDF.
This includes the 7 semimagic axisymmetric wazir tours shown on the Wazir Tours page.
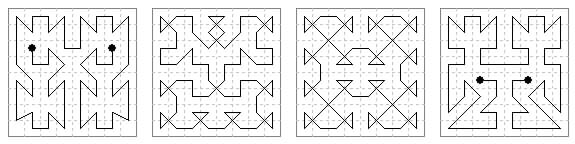
From this list I have extracted 125 geometrically distinct closed tours. These 125 tour diagrams will generate tours that are semimagic in the ranks if any bold link is numbered 1-16 or 16-1. The number at the bottom left is the first tour in Walter Trump's list that has this geometrical form. If there are k bold links in an asymmetric diagram this will generate 2×k semimagic tours. But this total must be divided by 4 in the case of a biaxial tour, or by 2 in the case of a tour with axial or 180 degree rotary symmetry, giving the number shown at the bottom right corner. These numbers account for 387 out of the 1346 arithmetically distinct semimagic tours.
16 Biaxial Tours, in pairs that are related by 90 degree rotation.
5 Rotary Tours.

8 Horizontal Axial tours

45 Vertical Axial tours
51 Asymmetric Tours

The above work shows that no magic king tour is possible on the 4×4 board.
In seeking a magic tour on this board it is natural to try to construct a magic king tour, since this uses the shortest moves, but perhaps surprisingly a magic king tour is impossible on the 6×6 board. It becomes possible only on the 8×8.
In the Magic Theory page we give a general proof that shows in particular that it is impossible to construct a 6×6 magic tour with rotary symmetry (known as an 'associated' square). That is a tour where numbers in diametrally opposite cells are complementary, adding to 37.
However it also proves impossible to construct a 6×6 magic king tour with axial symmetry. The best that can be done is a symmetric tour with 6 ranks and four files magic, which might be called 10/12 or five sixths magic.
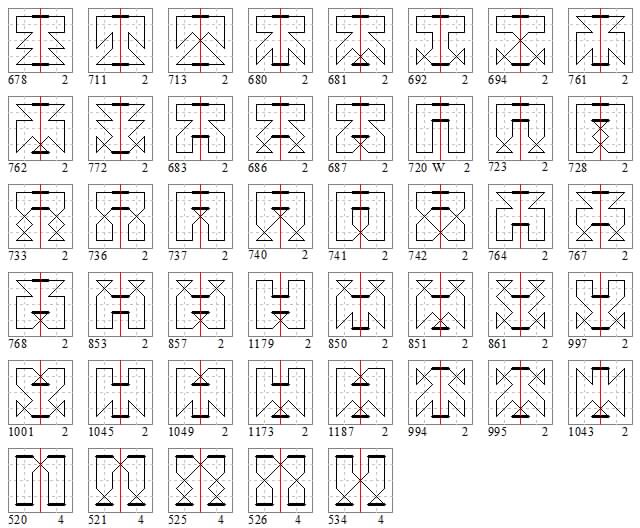
Four examples of of semimagic king tours of this type were sent to me (May 2022) by Andrew Usher. These have end-separation move {0,3}. In these the two middle files are non-magic, adding to 110 and 112, that is 111 ± 1, which is as near to magic as can be achieved.
These from left to right differ only in the horizontal exchanges 18-19 and 17-20, while from top to bottom they differ only in the vertical exchanges of 32-05 and 06-31. Their diagonal sums are 101 and 121 that is 111 ± 10 (left pair) and 105 and 117 that is 111 ± 6 (right pair).
Subsequently (September 2022) Walter Trump reported enumerating 58,319,963 geometricallly distinct semi-magic king tours on this board. That is tours magic in the ranks but not all the files. Among these semi-magic 6×6 tours he finds 3028 (82 closed) which have 6 magic ranks and 4 magic files. These are listed on the attached PDF: Trump 6×6 PDF. The Usher tours prove to be numbers 2050, 2051, 2122, 2123 in this list.
To avoid duplication it is usual to follow the Frénicle convention of orienting the tours with the smallest number at the top left, and with the number to its right smaller than the number below the corner. However this can result in an axially symmetric tour being arranged with the axis horizontal. It is preferable to have the axis vertical for ease of visual recognition. So we take this rule to override the Frénicle convention in these cases, but the smallest corner is still at the top left.
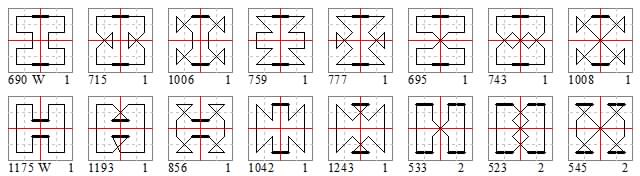
In the following diagrams I show open symmetric king tours from the Trump list. The tours that have the mddle two files non-magic occur in groups of eight related by transposition of the pairs of complements on these middle files.
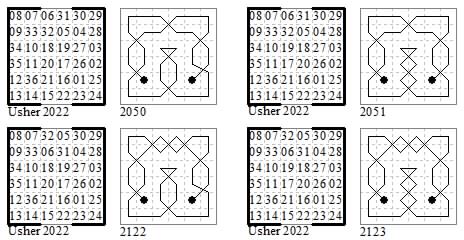
Tour #245 is the first symmetric tour in the list. #246 differs only in the transposition of 18-19. #247 transposes 17-20. #248 makes both these transpositions. #249 transposes 16-21. #250 transposes 16-21 and 18-19. #251 transposes 16-21 and 17-20. So the first eight tours only differ in the twists given to the king moves in the middle two non-magic columns. #252 being the most straight-forward wazir type.
The sums and patterns of the central columns are #245 XOO: 110, 113; #246 XOX: 110, 112; #247 XXX: 112, 110; #248 XXO: 113, 109; #249 OXO: 114, 108; #250 OXX: 115, 107; #251 OOX: 117, 105; #252 OOO: 118, 104. These totals are the same for each group of eight tours. The nearest to magic are the second and third, where the pattern of intersections is XOX or XXX.
From the Trump list we find 1024 symmetric open semimagic king tours. They occur in 128 groups of 8 differing only in the two central files. A concise way of showing them all graphically therefore is as 8 groups of 16, showing just the first in each group of eight.
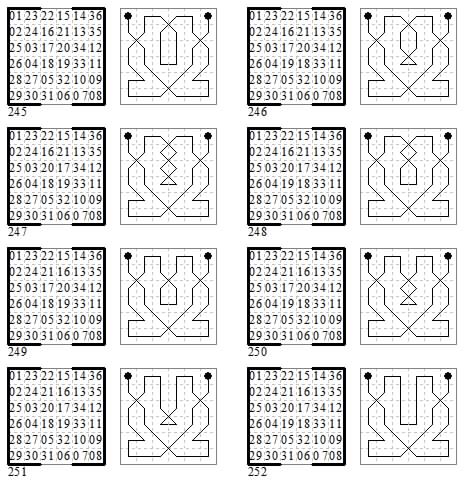
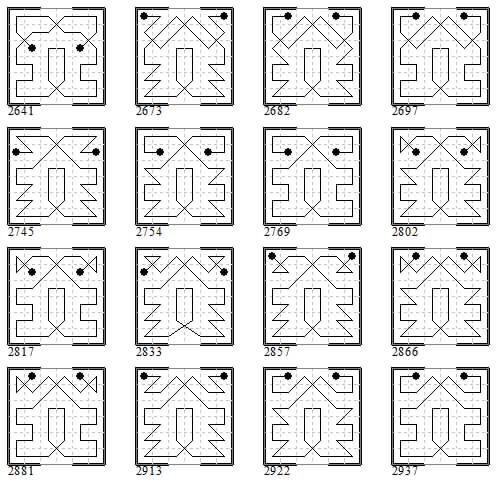
The first sixteen groups of eight tours related by transpositions in the middle two non-magic files in this way are 245-252, 253-260, 277-284, 285-292, 409-416, 417-424, 433-440, 441-448, 465-472, 473-480, 489-496, 497-504, 521-528, 529-536, 545-552, 553-560. Here we show just the first, the XOO type, in each group.
Second batch of sixteen groups of eight: 577-584, 585-592, 609-616, 617-624, 641-648, 649-656, 737-744, 745-752, 769-776, 777-784, 801-808, 809-816, 825-832, 833-840, 858-872 (all even), 873-887 (all odd). Showing the first in each group.

Third batch of sixteen groups of eight: 889-896, 930-944 (all even), 945-959 (all odd), 961-968, 993-1000, 1001-1008, 1033-1040, 1042-1056 (all even), 1057-1071 (all odd), 1249-1256, 1258-1272 (all even), 1273-1287 (all odd), 1313-1320, 1321-1328, 1354-1368 (all even), 1369-1383 (all odd). Showing the first in each group.
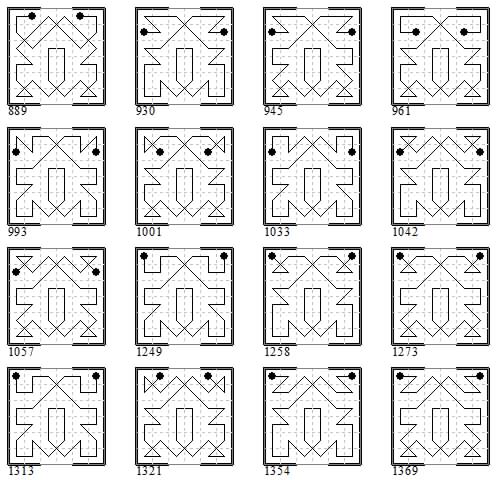
Fourth batch of sixteen groups of eight: 1385-1392, 1438-1452 (all even), 1453-1467 (all odd), 1485-1492, 1494-1508 (all even), 1509-1523 (all odd), 1541-1548, 1565-1572, 1589-1596, 1598-1612 (all even), 1613-1627 (all odd), 1646-1660 (all even), 1661-1675 (all odd), 1677-1684, 1685-1692, 1693-1700. Showing the first in each group.

Fifth batch of sixteen groups of eight: 1717-1724, 1725-1732, 1749-1756, 1765-1772, 1773-1780, 1797-1804, 1805-1812, 1893-1900, 1901-1908, 1925-1932, 1933-1940, 1949-56, 1973-1980, 2017-2024, 2033-2040, 2049-2056. Showing the first in each group.
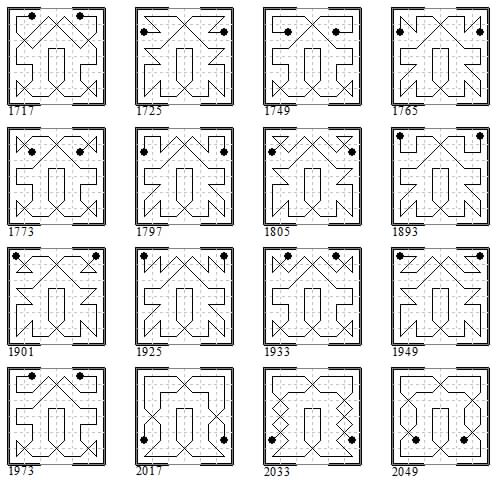
Sixth batch of sixteen groups of eight: 2089-2096, 2105-2112, 2121-2128, 2146-2160 (all even), 2161-2175 (all odd), 2178-2192 (all even), 2193-2207 (alll odd), 2210-2224 (all even), 2225-2239 (all odd), 2242-2256 (all even), 2257-2271 (all odd), 2289-2296, 2298-2312 (all even), 2313-2327 (all odd), 2345-2352, 2369-2376. Showing just the first in each group.
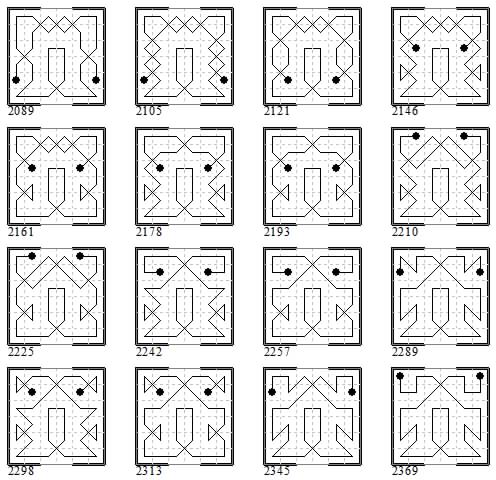
Seventh batch of sixteen groups of eight: 2393-2400, 2402-2416 (all even), 2417-2431 (all odd), 2450-2464 (all even), 2465-2479 (all odd), 2489-2496, 2497-2504, 2513-2520, 2521-2528, 2545-2552, 2553-2560, 2569-2576, 2577-2584, 2594-2608 (all even), 2609-2623 (all odd), 2626-2640 (all even). Showing just the first in each group.
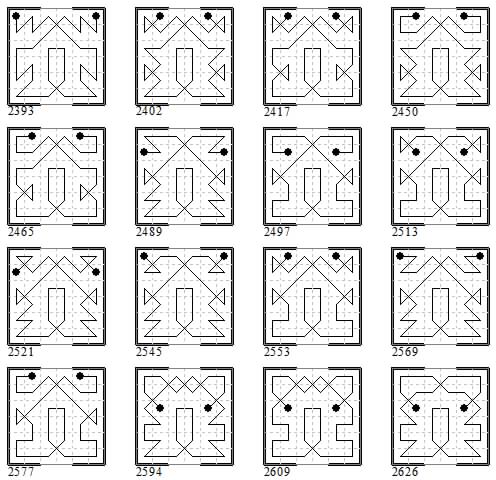
Eighth batch of sixteen groups of eight: 2641-2655 (all odd), 2673-2680, 2682-2696, 2697-2711 (all odd), 2745-2752, 2754-2768 (all even), 2769-2783 (all odd), 2802-2816 (all even), 2817-2831 (all odd), 2833-2840, 2857-2864, 2866-2880 (all even), 2881-2895 (all odd), 2913-2920, 2922-2936 (all even), 2937-2951 (all odd). Showing just the first in each group.
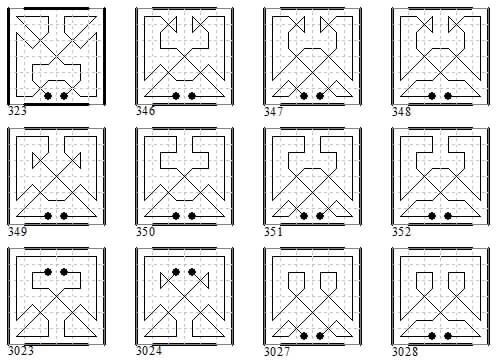
The 82 closed tours are: 301-305 (5), 315-316 (2), 323-328 (6), 344-352 (9), 2969-3028 (60). In the diagrams below these are oriented as shown in the list (not according to the Frénicle rule which often results in the reverse numbering of asymmetric tours having a different orientation).
Among these closed tours twelve are symmetric: 323, 346-352, 3023-3024, 3027-3028. These all have the outer files non-magic. In 323, 3023, 3024 the outer files add to 77 and 145 (that is 111 ± 34). In the others the sums are 118 and 104 (that is 111 ± 7).
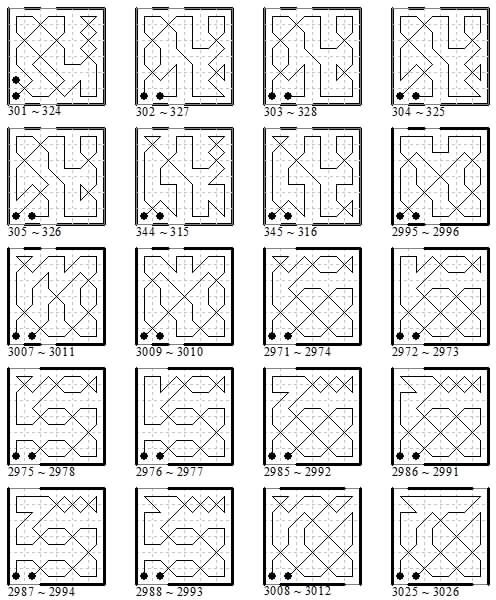
There are 70 asymmetric closed tours. These of course occur in pairs that are reverse numberings of each other. The first number cited is the tour with 1 in the corner cell, the second is its reverse with 36 in the corner.
The first pair 301/324 has the 1-36 link vertical and the nonmagic files, which are the first and third, add to 103 and 119 (111 ± 8). The others all have 1-36 horizontal. The other three-digit tours also have the first and third files nonmagic, adding to 57 and 165 (111 ± 54), 75 and 147 (111 ± 36), 105 and 117 (111 ± 6). Three of the four-digit tours also have the nonmagic files 1-3 and we group these together, as shown by the gaps between the dark border lines.
The other four-digit tours with the nonmagic files 1-2 or 1-6 are also grouped together here. The 1-4 and 3-6 cases form the next batch of 15.
The 1-4 and 3-6 cases are shown together
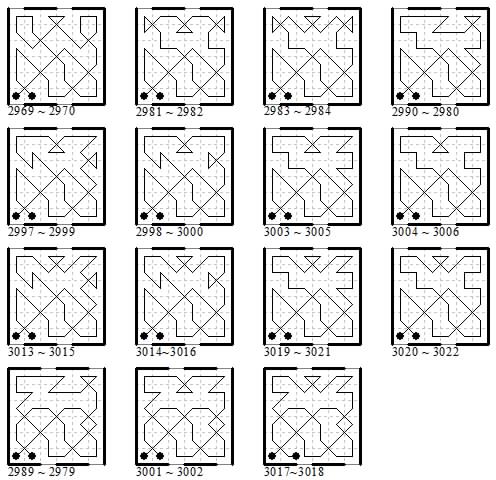
The sums of their nonmagic files in the four-digit cases can be 90 and 132 (111 ± 21), 96 and 126 (111 ± 15), 99 and 123 (111 ± 12), 100 and 122 (111 ± 11), 101 and 121 (111 ± 10).
The pairs of asymmetric closed tours are: 301-324, 302-327, 303-328, 304-325, 305-326, 315-344, 316-345, 2969-2970, 2971-2974, 2972-2973, 2975-2978, 2976-2977, 2979-2989, 2980-2990, 2981-2982, 2983-2984, 2985-2992, 2986-2991, 2987-2994, 2988-2993, 2995-2996, 2997-2999, 2998-3000, 3001-3002, 3003-3005, 3004-3006, 3007-3011, 3008-3012, 3009-3010, 3013-3015, 3014-3016, 3017-3018, 3019-3021, 3020-3022, 3025-3026.
There are very simple magic king tours on rectangular boards 2×2n. The columns consist of pairs of complements, adding to 4n+1, the first and last entries, 1 and 4n, being in the first column, and the middle entries, 2n and 2n+1, in the last column.

These tours were diagrammed in Chessics #26 p.117 and #30 p.163, but similar diagrams have long appeared in books on magic squares.
We begin with non-diagonal examples.
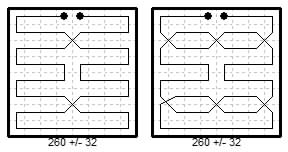
The two Magic king tours above are by M. B. Lehmann (1932).
These and the following are king tours of biaxial type that are magic in ranks and files.
The deviations from magic in the diagonals are noted.
The following are magic king tours of my own construction (Feb 1986).
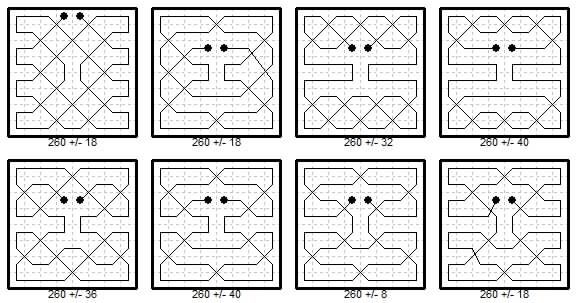
Requiring the diagonals to also add to the magic sum (as in the next section) allows less variety in the designs.

More magic king tours of my own construction (March 1986).
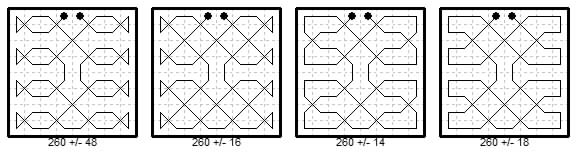
This is the class of magic king tours to which most attention has been directed. We give a catalogue here of all known examples. Thanks to work done by T. W. Marlow in July 1995 (reported in The Games and Puzzles Journal, issue 15, p264, December 1997) this is now believed to be the complete list for this type. However I have since discovered that considerable work on this subject was done in the 19th century and was published in French newspaper puzzle columns from 1882 onwards. However this work was presented in the form of cryptotour puzzles, without diagrams of the solutions, so has been overlooked since. For a partial decoding of this work see the version I published in the PDF version of these Notes made in 2019. Here I have decided to follow the account given by Tom Marlow.
The tours are classified here according to the numbers in the diagonals and the positioning of the end-cells of the quarters, where the numbers 1, 16, 17 32, 33, 48, 49, 64 occur.
A-cases. The first of the A-group was given by W. W. Rouse Ball in Mathematical Recreations and Essays, 7th edition, 1917, p133 [information from T. H. Willcocks]. The others are formed from it by interchanges of non-diagonal elements, as was indicated by M. B. Lehmann in Neue Mathematische Spiele: Der Geometrische Aufbau Gleichsummiger Zahlenfiguren, 1932, pp.360-362. The diagonal with the smallest number in it is: 4, 54, 55, 49, 17, 23, 22, 36. To find the entries in the other diagonal subtract from 65. Many other biaxially symmetric magic tours can be formed by slight variation, for instance by transposing 16-17 and 48-49 in A1, but these changes result in the diagonals no longer being magic.
B, C, D cases. The first B case is due to J.Brügge, Die Schwalbe, August 1985, pp505-509, and from this I derived the other, the diagonal is: 4, 51, 52, 55, 23, 20, 19, 36. This and the C and D cases were given by me in Chessics #26, Summer 1986, p.120. The diagonal in C is: 45, 4, 25, 24, 56, 57, 36, 13, and in D: 5, 54, 55, 48, 16, 23, 22, 37.

The E, F and G cases are due to Tom Marlow, as reported in The Games and Puzzles Journal, issue 15, p.264, December 1997. The diagonal in E is the same as for the D cases. The F diagonal is: 60, 12, 57, 1, 33, 25, 44, 28.
The G diagonal is: 60, 58, 11, 1, 33, 43, 26, 28. I keep to the numbering used in G&PJournal, though the diagrams are differently arranged; the cases with the join in the edge being shown first.

Thos diagram shows a diagonally magic king tour on a 16×16 board (G.P.Jelliss Chessics #26, p.120, 1986). It is derived from the A1 tour.

It is possible to construct diagonally magic king tours that are not biaxial, as in these axial examples from French newspapers of the 1880s. Four from Gil Blas, namely: three by 'X a Belfort' (Prof C. E. Reuss) problem 992 (10 Sep 1882) and problem 1006 (24 Sep 1882) with two solutions, and one by 'Mme Celina Fr' (Francony) problem 1013 (1 Oct 1882) the second solution to this problem is the biaxial case C1.
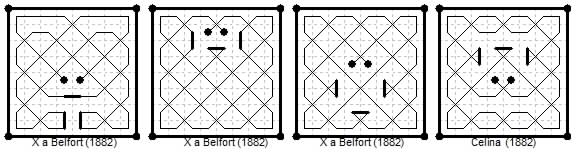
From Gil Blas four tours by 'X a Belfort' (Reuss) problem 1028 (16 Oct 1882) with four solutions.

Four from Le Galois. Two by 'X a Belfort' (Reuss) problem 34 (9/23 Sep 1882) and problem 41 (23 Sep/12 Oct 1882) in the 'Jeux D'Esprit' section. One by by 'MFA' problem 411 (18 Sep 1882) and another by 'Adsum' (Charles Bouvier) problem 466 (13/29 Nov 1882).

Four by 'X à Belfort' (Reuss) in Gil Blas problem 1035 (23 Oct 1882) with four solutions.

The patterns in many of these examples evidently follow to a great extent the same scheme as the arithmic king tours shown earlier. Two magic king tours by R. Dubief problem 85 (15/29 Jan 1883) and two by Galtier problem 106 (26 Feb/12 Mar 1883) in Le Gaulois follow.
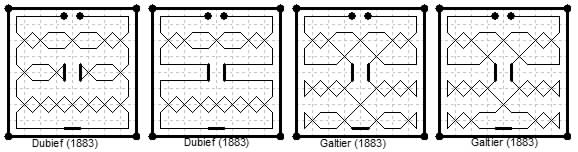
Four more by Galtier from Le Gaulois problem 267 (14/28 Jan 1884) and problem 288 (25 Feb/10 Mar 1884) each problem having two solutions.

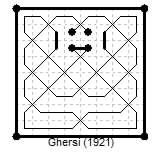
This later example appeared in Matematica Dilettevole e Curiosa by Ing. Italo Ghersi (published by Ulrico Hoepli, Milan, Italy, 2nd edition, 1921, p.320, figures 261 and 265).