
Here we gather together results concerning tours that use both knight moves and diagonal moves. We call these Princely tours since the Knight + Fers is known as a Prince, and the Knight + Bishop as a Princess (on the same principle as the distinction beteeen King and Queen, Emperor and Empress).
This is the simplest piece from the Bishop + Knight family.
2×3 board. There is an arithmic prince tour with biaxial symmetry. Whatever way it is numbered the files add to 5, 7, 9 (cd=2) and the ranks to 9 and 12.

8×8 board. A knight+fers tour was given by as Suli (c.900), together with a knight+alfil tour. These were the first tours by two-pattern leapers. They are reproduced in numerical form in H. J. R. Murray A History of Chess (1913) p.336. The FN tour is given here in diagram form. Similar tours also appear in other Indian and Turkish sources of later date, as in the one by the Rajah of Mysore.

This subject was rediscovered by P. B. van Dalfsen who published a symmetric solutions to thr fers and alfil problems in (Fairy Chess Review problem 9601, June 1953, p.74, solutions October 1953, p.93. My example is symmetric and uses the same pattern of knight moves as in my Hospitaller tour shown below.
It is easy to prove that the fers moves must form a fixed pattern of crosses: Just start at a1 and put in the only possible fers move, then go to c1 (which cannot join to b2) then go to e1 and so on; only the knight's moves vary.
Figured Prince Tour. W. E. Lester Fairy Chess Review (vol.3 #10 Feb 1938 p110 ¶3109). Prince (Fers+Knight) open tour of 5×5 and 8×8 with squares in sequence along diagonal.
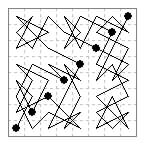
8×8 board. As noted in the Prince section above a Kight+Afil tour was first given by as-Suli (c.900), as shown in Murray's History of Chess (1913) p.336. In any alternating tour of this type the diagonal moves form the same fixed pattern of crosses; only the knight's moves vary. The topic was rediscovered by P. B. van Dalfsen who found a symmetric solution. My example is also symmetric and uses the same pattern of knight moves as in my Prince tour shown above.

To avoid ambiguity it has been necessary to curve the alfil moves in the above diagrams.
Symmetric alternating tour on the 6×6 board (Jelliss 12 August 2022). The bold lines indicate where the {3,3} moves overlap.

8×8 board. I sent this and the above Prince and Hospitaller results to Stefanos Pantazis for the US Probem Bulletin on 14 Jun 1993, but I don't think they were ever published there. The alternating Kight+Commuter tour here is in numerical form because of difficulty in showing it graphically. As with the Knight+Fers and Knight+Alfil tours above the diagonal commuter {4,4} moves similarly form a fixed pattern in alternating tours.

As reported in the first online issue of the Games and Puzzles Journal (#19, Jan-Apr 2001) #19 Prof. D. E. Knuth improved on the above result by findin these two symmetric knight formations that will combine with all three cases: alternating Fers, Alfil and Commuter to give tours (and with other properties - see the article).