
by George Jelliss [August 2022]
This page is based on the Queen Tours section in the 2019 PDF on Walker Tours.
Some of the the tours were previously on the page now devoted to Rook Tours.
Latest update [17 October 2022] adds some King + Dabbaba magic tours derived from semimagic king tours.
Some new results by Walter Trump on magic queen tours on 5×5 and 6×6 boards have been added. These were circulated in two lists, issued by Walter Trump from Germany to Joachim Brügge and others interested in magic squares and tours. The first [2 June 2022] lists 31 queen tours on the 5×5, all that are possible on this board. The second [9 June 2022] lists 110 queen tours on the 6×6, of a special type formed of ranks consisting of complementary pairs (adding to 37). From these lists I show here only the strictly symmetric tours and those with five or fewer types of move. The 6×6 tours, all being very similar in structure, are shown in simpler typewritten form, instead of on more elaborate diagrams. Walter Trump maintains a website for devotees of magic tours: http://www.trump.de/magic-squares/index.html.
Magic tours with 180 degree rotational symmetry are impossible on the 6×6 board (and in fact on any bosrd of side 4k + 2). [There is now a general proof of this on the Theory of Magic page.] The 6×6 tours from Walter Trump's list have axial symmetry, the ranks all being composed of pairs of complements, the 1st and 6th, 2nd and 5th, 3rd and 4th, adding to 37.
Sections on this page: — What is a Queen? — Two Move Queens — Three Moves — Four Moves — Five Moves — Six Moves — Seven Moves
Any piece with both lateral and diagonal moves at least one being longer than a king move can be regarded as a type of Queen. We arrange the tours here according to the number of different moves and secondarily by the size of the board used. It is more usual, for instance in the study of magic squares, to arrange the material accoording to board size, but from the point of view of tours it is the moves used that are significant. It may be questionable whether a pattern formed with more than four types of move can properly be called a 'tour'. The moves used by each piece are listed with Lateral moves first followed by Diagonal moves.
In Chessics #26 (p.119, 1986) I noted the following two magic tours (necessarily non-diagonal) by this double-pattern mover. They show biaxial symmetry when the end-points of the path are joined up to give a closed path. The black dots mark 1, 8, 9, 16.

Biaxially symmetric 4×8 magic tours. Results from a partial enumeration (18 Oct 2014). The alfil moves are curved to avoid overlapping.

The {1,1} mover is restricted to cells of one colour, and the {0,3} mover to one in nine of the cells on a large board. But the {1,1}+{0,3} mover can reach every cell. making it an 'amphibian'. It first appeared in a leapfrog puzzle given by A. C. Pearson in The Twentieth Century Standard Puzzle Book (1907 part 3 p.62). Being the simplest possible 'amphibian', the name 'Frog' seems appropriate.
On the 2×4 board there is one biaxial tour. It is semi-magic. In Chessics #26 I noted the following 4×4 magic frog tour (necessarily non-diagonal) showing biaxial symmetry.

Two 4×6 biaxial magic Frog tours that I found 10 Aug 1991. File sum 50. Rank sum 75. The first is also given by Trenkler (1999). Besides the magic numberings they each have a quasi-magic numbering, the rank sums of the first being 63 and 87, and the second 39 and 111. The {0,3} moves are curved or dashed to avoid overlap. These were among a series of 29 by two-pattern movers that I found.
The same is possible on the 4×8 board. File sum 66, rank sum 132.

A 5×5 (non-magic) symmetric open tour by another amphibian.

2×3 board. On this board besides the two {0,1}{0,2} wazaba rook tours there are two other semi-magic queen tours. When closed these open tours give only one geometrically distinct axially symmetric closed tour. There are also four other closed tours. One rotary and three asymmetric.

2×4 board. On this board by permuting the files of the magic king tour we can form two magic queen tours. The numbers in the ranks are 1,4,6,7 and 8,5,3,2 which are the only sets of four adding to 18 that do not consist of two complementary pairs adding to 9, which are needed for the files. There is also a biaxial tour 2×4 tour, which can be numbered to be semi-magic in either ranks or files.
6×6 board. Here we show six magic tours derived from the semimagic king tours listed by Walter Trump. First a batch of tours that introduce a pair of dabbaba moves. The dabbaba moves are shown here as a bent line instead of a curve.


More examples can probably be added here when more of the king tours have been examined.
8×8 board. Magic tour Jelliss (2001) derived from the augmented knight {0,1}{0,2}{1,2} tour by Wallis (1908) by interchanging 2-3 and 6-7 files which transforms knight {1,2} moves to fers {1,1} moves.

By permuting the files of the 2×4 magic king tour we can form a magic biaxial tour by this piece when numbered about the short axis. About the long axis it is only magic in the ranks. There is also another biaxial tour which is semi-magic.

One of the 4×4 magic squares (#2 in the Frénicle list) that is a diamagic queen tour.

Magic biaxial rectangle tour 4×6 by L. S. Frierson in Andrews (1917, Fig.272 reflected). Sums 50 and 75.

Walter Trump's list of 31 diagonally magic tours on the 5×5 board includes this beautiful tour, #22, which is the only one using three move types. It has 180 degree rotational symmetry, having 13 at the centre and diametrally opposite cells adding to 26. Only half the tour is shown in the line diagram here. See later for the two other symmetric tours using five move types.

This is the smallest three-pattern amphibian. Half of a closed 16×16 tour (Jelliss Chessics #24 1985 p.98) is shown. This half-tour has 180 degree rotary symmetry, the middle move 64-65 passing through the centre. The second half begins with 129 on the top left or bottom right corner, and reflects the first half, so the tour overall has axial symmetry.

The name 'pterodactyl' was proposed because of the spiky nature of the tour.
The middle move of the second half is 192-193. Diametrally opposite cells add to 129 or to 385, while axially opposite cells add to 257. The 128-129 move and the closure move 256-1 are the only {0,15} moves used.
One of the 4×4 diagonally magic squares (#619 in the Frénicle list) is a magic queen tour. It has axial symmetry. The longer moves of two or three steps are shown here by broken lines.
Diagonally magic 8×8 tour by four-move queen (Jelliss 26 Feb 1986). The files consist of pairs of complements adding to 65. The ranks are formed of pairs adding to 97 and 33. The {0,2} and {0,3} moves are shown curved, to avoid overlapping.

Jelliss (2001) diamagic queen alternating rook-bishop tour derived from Wallis (1908) alternating knight-rook tour by interchange of the 2-3 and 6-7 ranks, and rotation 90° to conform to the Frénicle convention.

Two diamagic four-move queen tours (Jelliss Chessics #26 p.120 1986) showing mainly diagonal moves. The files consist of pairs of complements adding to 65. The ranks are formed of pairs adding to 33 and 97. The lateral moves {0,2} and {0,7} are shown by dashed lines. The {0,7} moves form the middle link 32-33 and the closure link 64-1.

The second version transposes the two numbers at the end of each diagonal, e.g. 9-10 to 10-9.
Another diagonally magic four-move queen tour (Jelliss, Chessics #26, p.120, 1986) showing mainly lateral moves (1-3-rook, 1-2-bishop). The {2,2} and {0,3}moves are shown by dashed lines. The files consist of pairs of complements adding to 65. The ranks are formed of pairs adding to 97 and 33. The {0,3} moves are the middle 32-33 and closure 64-1.

These tours, which go over the limit of four move types, mark a transition from the study of tours to the study of magic squares.
The Lateral and Diagonal moves used are listed in an abbrevated form. Those with the most lateral moves are listed first.
Diamagic queen tour using 5 move types (L 1 2 3 7 + D 1) by J. Brügge Die Schwalbe Aug 1985. In the diagram the three types of longer rook moves are curved.

Tours #11, #49 and #104 from Walter Trump's list of 6×6 tours.
15 24 23 14 13 22 11 27 25 12 10 26 28 07 08 29 30 09 06 32 33 04 05 31 35 01 03 34 36 02 16 24 19 18 17 21 |
15 23 24 13 14 22 36 03 02 35 34 01 04 31 32 05 06 33 30 09 08 29 28 07 10 26 25 12 11 27 16 19 20 17 18 21 |
15 24 23 14 13 22 35 03 01 36 34 02 04 31 32 05 06 33 30 08 09 28 29 07 11 25 27 20 12 26 16 20 19 18 17 21 |
Here are the other two symmetric queen tours on the 5×5 board in Walter Trump's listing (see the 3-move queen tour shown earlier). They use three lateral and two diagonal moves. These tours are #20 and #21 in the list. All other tours in the list are asymmetric and use 5, 6, 7, or in one case 8 moves.
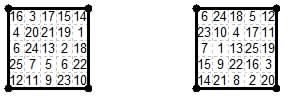
This 123/12 queen also occurs in eight 6×6 diagonally magic tours in the list from Walter Trump.
Tours #4, #10, #33, #34, #39, #41, #83, #85
06 05 33 04 32 31 35 34 01 36 03 02 28 29 07 30 08 09 17 18 21 16 19 20 11 12 27 10 25 26 14 13 22 15 24 23 |
06 05 33 04 32 31 35 34 01 36 03 02 28 29 07 30 08 09 16 18 20 17 19 21 11 12 27 10 25 26 15 13 23 15 24 22 |
08 09 30 07 28 29 26 25 10 27 12 11 31 32 04 33 05 06 23 24 15 22 13 14 03 02 36 01 35 34 20 19 16 21 18 17 |
08 09 30 07 28 29 26 25 10 27 12 11 31 32 04 33 05 06 22 24 14 23 13 15 03 02 36 01 35 34 21 19 17 20 18 16 |
02 01 34 03 36 35 32 33 06 31 04 05 09 08 30 07 29 28 20 19 16 21 18 17 25 26 10 27 11 12 23 24 15 22 13 14 |
02 01 34 03 36 35 32 33 06 31 04 05 09 08 30 07 29 28 21 19 17 20 18 16 25 26 10 27 11 12 22 24 14 23 13 15 |
01 02 34 03 35 36 32 33 06 31 04 05 09 08 30 07 29 28 21 19 17 20 18 16 26 25 10 27 12 11 22 24 14 23 13 15 |
01 02 34 03 35 36 32 33 06 31 04 05 09 08 30 07 29 28 20 19 16 21 18 17 26 25 10 27 12 11 23 24 15 22 13 14 |
Magic 6×6 queen tour (Jelliss 16 Mar 1986) with diagonals 60 and 162 (that is 111±51).

Tours #32 and #50 in Walter Trump's list of 6×6 diagonally magic tours.
12 10 26 11 27 25 29 30 09 28 07 08 36 35 03 34 02 01 13 14 22 15 23 24 04 06 32 05 31 33 17 16 19 18 21 20 |
02 03 01 36 34 35 20 21 19 18 16 17 32 31 33 04 06 05 25 27 26 11 10 12 24 22 23 14 15 13 08 07 09 28 30 29 |
Magic 6×6 queen tour (Jelliss 16 Mar 1986) with diagonals 60 and 162 (that is 111±51.

Tours #54 and #100 from Walter Trump's list.
01 34 35 02 03 36 26 10 12 25 27 11 09 30 29 08 07 28 31 04 05 32 33 06 24 15 14 23 22 13 20 18 16 21 19 17 |
12 27 26 11 10 25 35 03 01 36 34 02 04 31 32 05 06 33 30 09 08 29 28 07 13 22 23 14 15 24 17 19 21 16 18 20 |
Magic 6×6 queen tour (Jelliss 16 Mar 1986) with diagonals 60 and 162 (that is 111±51) and with diagonals 96 and 126 (that is 111±15).

Diamagic queen tour with 5 move types by L. S. Frierson in Andrews Magic Squares and Cubes (1917) Fig.268, consists mainly of 8 repetitions of an 8-cell king-path.

Magic 6×6 queen tour (Jelliss 16 Mar 1986) with diagonals 102 and 120 (that is 111±9).

This is one of a series of 10 magic queen tours I constructed on the above date using five or six move types. This has {5,5} moves along the diagonals, crossing at the centre.
Diamagic queen tour using 5 move types (6 including the closure move) by J. Brügge.

Die Schwalbe Aug 1985. The {5,5}moves are dashed. The {2,2} and {0,5} moves are curved.
Magic 6×6 queen tours (Jelliss 16 Mar 1986) with diagonals 110 and 112 (that is 111±1) and diagonals 102 and 120 (that is 111±9).

An 8×8 diamagic queen tour with 6 move types by Joachim Brügge Die Schwalbe Aug 1985. Diametrally opposite cells add to 65 (i.e. Bergholtian symmetry). Four pairs of numbers in the files add to 33 and 97, and in the ranks to 49 and 81.

In the diagram only the end sections of the long diagonal moves are shown.
8×8 diamagic queen tour by Joachim Brügge Die Schwalbe 1985, based on Durer's 4×4 square.

Magic 6×6 queen tour (Jelliss 16 Mar 1986) with diagonals 114 and 108 (that is 111±3).

This 8×8 diamagic queen tour with 7 move types is a slight modification of a non-diamagic tour given by J. Brügge (Die Schwalbe Aug 1985), it is based on spirals (Jelliss Chessics #30 p.163 1987).

Magic 6×6 queen tours (Jelliss 16 Mar 1986) with diagonals 87 and 135 (that is 111±24) and diagonals 69 and 153 (that is 111±42).

I'm not sure of the value of these examples of more-move magic Queen tours, included in the PDF on Walker Tours, that use six or more moves, but have had second thoughts and decided to include them here after all.