This page gathers together square tours, mostly magic, that use three or more different move types, including at least one 'big beast' move. They are arranged according to the board size. However, the 4×4 case has its own page, including a full catalogue of the diagonally magic aquares. Several examples are shown here of 12×12 magic tours derived from 4×4 magic squares by Joachim Brugge's remarkable braid extension method.
Sections on this page: — 6x6 — 8x8 — 9x9 — 10x10 Wizard — 12x12 — 20x20 — 24x24
I have a note that T. H. Willcocks composed a 6×6 tour with these moves but I have lost the reference.
Here are some I made myself (Jelliss 12 August 2022), all with rotary symmetry (but not birotary).
The first of these has the fers moves in regular 9-cross formation as in the Princely tour examples.

Here are eight magic 6×6 tours derived from semimagic king tours where the non-magic files are the outer ones,
so transposition between them results in the added moves being the longer {1,5} type.
The first case also uses {0,4} amd {1,4} moves.
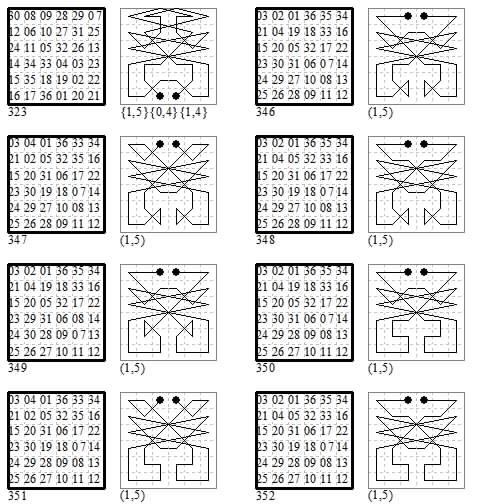
Another way of using king moves to help generate magic tours to make a king tour on each 2×2 block, and to join these up with longer moves, so that the pattern of links between them is similar to that of the 3×3 magic square. This method was used by Falkener in 1892.
The best I've achieved by this method use only four move types. They also have one of the diagonals magic. They use {1,2} and {3,4} moves besides the {0,1} and {1,1}. The end separation move is a fifth type {1,3} a camel move in each case. One diagonal adds to 112 instead of 111.
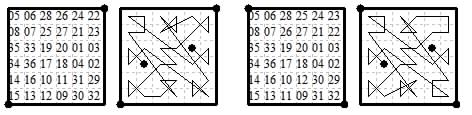
(1) The earliest tour of this type is by Edward Falkener in Games Ancient and Oriental 1892
(p.294 rotated 90° here to conform to the Frénicle rule).
The diagonal sums are 108 and 114 (that is 111±3). This uses five move types: {3,4}{2,4}{1,1}{2,2}{0,1}
and the end separation {0,3} is a sixth.
(2) With five types of move it is possible to achieve a diagonally magic tour of this type.
The moves used are {1,2}{2,4}{0,2} besides the King moves, These are the moves of a Nightrider + Queen, also known as the 'Queen of the Night'.
The closure move is a sixth type {0,5}.
(3 and 4) The third and fourth diagonally magic tours of Falkener type shown here also use five move types:
{3,4}{0,2} together with {0,3} or {3,3} and the king moves {1,1}{0,1}. These make a piece that is Queen + Antelope in each case.
The end separation is a sixth type, {0,5} or {0,3}.

(5) This diagonally magic tour of Falkener type uses five move types {3,4}{2,4}{0,2} + king moves, that is Queen + Lancer + Antelope.
A sixth type is used as closure move {0,5}
(6) Another Falkener style diamagic tour using 6 types of move {1,4}{2,4}{3,3}{0,2} plus king moves, that is Queen + Lancer + Giraffe.
The closure is a seventh move {0,3}.
It is possible to transform a Falkener style tour by changing the King moves {0,1} (1,1} to {0,3}, {3,3} links.
These are more difficult to show diagrammatically since the moves overlap. This transform applied to a tour using 5 move-types
produced this diamagic tour that uses only 4 types of move. {1,2}{3,3}{0,1}{0,3} with end separation {0,5}.
This can be described as an Queen + Kmght (Empress) tour. Only the ends of the three-unit moves are shown, and the {0,1} links are curved.
We also show another tour of this transformed tyoe. Only the initial moves and the links between the blocks are shown here.
This uses six types of move: {1,2}{2,4}{3,3}{2,2}{0,1}{0,3). This is an Empress + Lancer tour. The end separation move is a seventh type {0,5}.
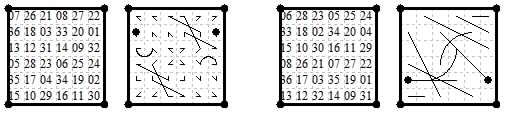
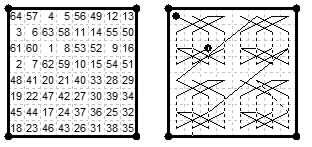
We show two other examples using different methods. The first shows a nondiagonal magic tour using only four move types {2,5}{1,1}{0,1}{0,2}
with a fifth type {0,5} as end separation. This is based on aother Falkener tour (1892 p.292), permuted and reoriented. The diagonals add to 100 and 133.
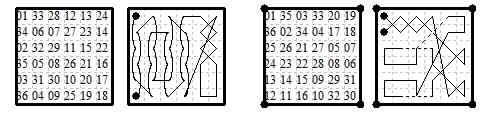
The diagonally magic example is from Andrews (Fig.321) but I have reversed the numbering so that 1 is in the corner instead of 36.
It uses six move types. {1,5}{2,4}{1,1}{2,2}{0,1}{0,2}. The end points are a wazir move apart making it a reentrant tour.
There are many tours to be found in works on magic squares that use even more types of move, but larger numbers are only justified if they are needed to show features that cannot be more clearly shown by using fewer.
8×8. Magic four-camel tour from Le Siècle (13/14/21 May 1887) by 'Adsum a Saint-P' (Bouvier) symmetric about the vertical axis. Diagonal sums complementary (adding to 520). This is the earliest mention of a {1,3} mover that I know of.
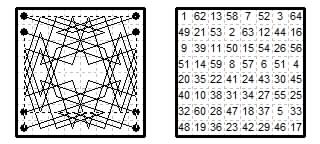
8×8. Diamagic four-knight tour from Le Siècle ¶4820 (15 Jan 1892) by Adsum (Bouvier).
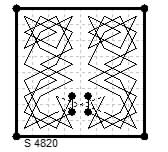
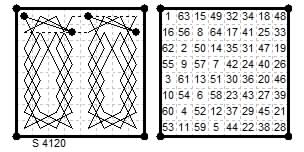
Diamagic four-knight tour from Le Siècle ¶4120 (24 Jan 1890) by Adsum (Bouvier).
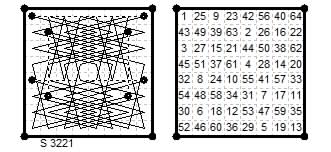
8×8. Diamagic four-giraffe tour from Le Siècle ¶3221 (5/12 Mar 1887) by 'X a Belfort' (Reuss) symmetric about the vertical axis.
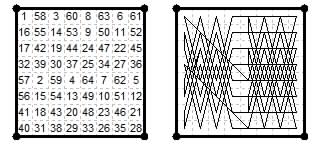
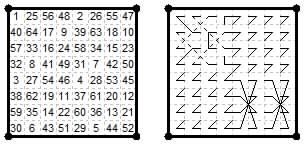
8×8. The following remarkable magic square is due to H. J. Kesson ('Ursus') 'Caissan Magic Squares' The Queen, The Lady's Newspaper, London, Aug, Sep, Oct 1881. It uses Giraffe moves combined with lateral and diagonal moves. Besides adding to the magic constant in ranks and files (rook moves) it is also magic in the all 16 diagonals, and also magic in the knight and camel lines. As noted in the Magic Squares section (PDF#1) it has the same numbers in the ranks as the 'Intermediate' magic square of the semi-natural type. This tour is also in Andrews (1917, Fig.262)
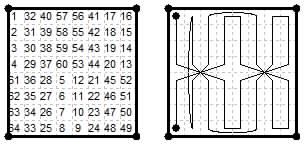
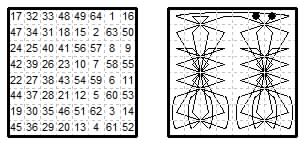
A diamagic camel + four queen-move types: by L. S. Frierson in Andrews Fig.270.
A quasi-magic multileaper square by James Parton (Andrews Fig.97) using five different move types plus {0,7} closure. Ranks magic (4×65), files 260±4 (4×64 and 4×66).

Diamagic multileaper tour with 6 move types by L. S. Frierson in Andrews Fig.267.
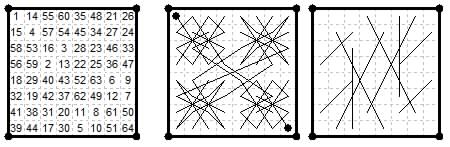
8×8. Diamagic Queen + Camel tour by L. S. Frierson in Andrews Fig.265. Only the ends of the {0,4} and {4,4} are shown. Each successive 4 numbers occupy the corners of a square 5×5.
8×8. A magic tour by Benjamin Franklin (Andrews Fig.183, 191, 291). Diagonals 228 and 292 (sum 520). All 2×2 sub-squares add to 130.
8×8. Diamagic tour by L. S. Frierson [Andrews Fig.449]. The {0,5} {2,2} {3,6} links that pass over intermediate cells are shown separately. Closure move {7,7}
8×8. Panmagic associated square by L. S. Frierson [Andrews Fig.468]. All the odd moves are horizontal moves of {0,4} type, which overlap and are indicated here by a single dotted line. The closure move is {7,7}. If the files are permuted so that the {0,4} moves are closed up to become {0,1} moves (the files being taken in the sequence 1,5,2,6,3,7,4,8) as in the right-hand numerical diagram the tour remains diamagic and associated (no longer panmagic) but uses 9 move types.
This diamagic square is Fig.96 in Andrews (1917) roted by a half-turn, and is formed of nine 3×3 magic squares linked as if the nine 3×3 components are cells of another 3×3 magic square. The three moves of the small square are thus augmented by three longer moves. A seventh move {0,8} being needed to make the tour closed

The wizard is a multimover able to make any leap {r,s} where r and s have no common factor. In contrast the witch makes only moves {r,s} where r and s have a common factor. This means that a witch move passes over the centre of at least one intermediate cell. The wizard's moves were first illustrated on the cover of Chessics #24 (Winter 1985), the special issue on Theory of Leapers.
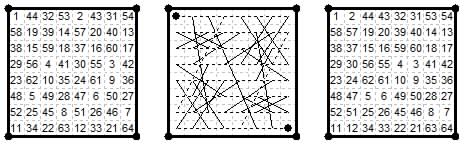
The magic wizard tour problem begins from the 10×10 magic square formed of two orthogonal latin squares, found by Ernest Tilden Parker 1960. It is shown in a modified form as the frontispiece in the later editions of Rouse Ball's Mathematical Recreations. The original version in the 1960 paper shown here is almost symmetric, number ab being opposite ba, except in the corner 3×3 area. Diagonals not magic.
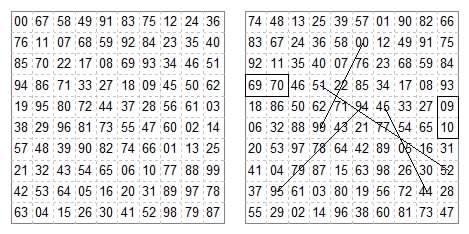
The problem is to permute the ranks, or the files, or the initial digits, or the final digits, or any combination of these so as to produce a Wizard Tour. The best result I have found to date by permuting the ranks and files is shown on the right. It uses only four witch moves (or three if the closure move 99-00 is not counted). Can the number be reduced to zero? There is always one wazir move in a rank and one in a file, 69-70 and 9-10 in the case shown.
12×12. (Jelliss 2018) Brügge method tour using a P or R pattern braid based on Frenicle #24.
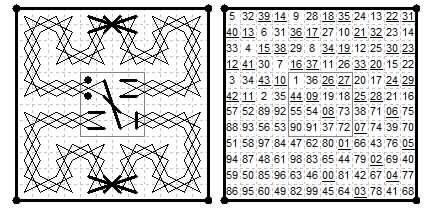
12×12. Diagonally magic tour (Jelliss 2018) based on 4×4 Emperor diagonally magic tour by variant of Joachim Brügge method (braids forming G shape instead of S). Closure {0,3}.
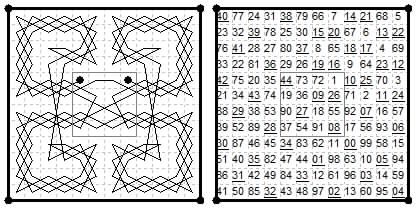
(Jelliss 2018) Brügge method tour using P or R pattern braid, using Frenicle #6.
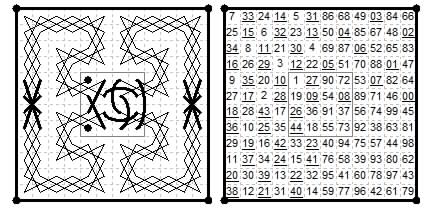
12×12. The original Joachim Brügge tour by adding a braid to a 4×4 magic square.
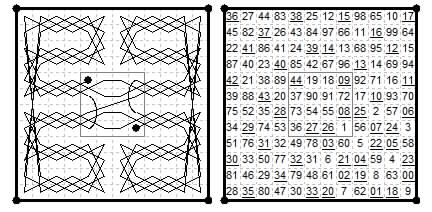
This is derived from the Durer 1514 magic square (Frenicle #175) in the 4×4 centre. {3,3} closure move.
12×12. The magic constant for the 12×12 board is 870. Using the diamagic 4×4 Emperor tour joined to copies of itself in a 3×3 magic array (after Andrews Fig 98). Moves {0.1} {1,2} (two moves within the 4×4) plus four different joins). Also {3,8} closure move.

This diagonally magic ornamented square by Charles Planck is shown (in numerical form) as Fig.700 in Magic Squares and Cubes by W. S. Andrews (1917). The {2,2} move is used only for the middle move 200 to 201 (a3-c1) and the closure move.
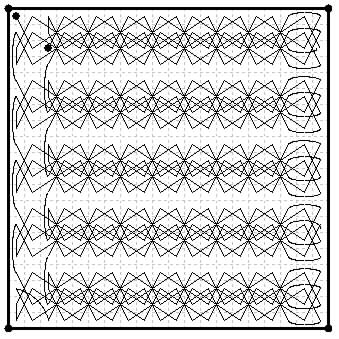
Diamagic square by Charles Planck (Fig.701 in numerical form in Andrews 1917). The {0,2} and {2,2} used for the middle move 288 to 289 and closure, are shown in bold.