
This page gathers together oblong tours, mostly magic, that use three or more different move types, including long leaps. They are arranged according to the dimensions of the boards used. The main aim has been to reduce the number of different types of move used in the magic rectangles.
According to T. R. Dawson's review in FCR (February 1936 p.174) E. Huber-Stockar made "a really remarkable study on partially generalised knights and their tours" in the Comptes Rendus du Premier Congres International de Recreation Mathematique, 1935, which was edited by M. Kraitchik. I have not seen the complete article but numerous tours of multiple leapers, with moves in given directions, by Huber Stockar were published posthumosly in the pages of FCR. I am not clear if these were all original or first appeared in the Comptes Rendus. These tours are not magic, just very tightly controlled.
Sections on this page: — 2x4 — 3x5 — 3x7 — 3x9 — 4x6 — 4x8 — 5x7 — 5x8 — 7x9 — 8x12
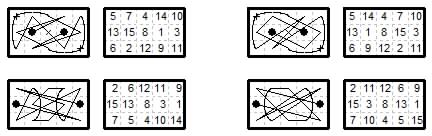
2×4. Two semi-magic biaxial closed tours by WDC (Wazir + Dabbaba + Camel).

2×4. This WFC mover (camel + king) can make a closed 2×4 tour with axial symmetry that is a magic in ranks and files when numbered in two ways (these are permutes of the magic king tour) and also semi-magic in the ranks when numbered from other cells. It also produces two semi-magic biaxial closed tours, similar to the camel + rook examples.

2×4. This three-way WNC moving piece has two semi-magic biaxial closed tours.

2×4. This camel + restricted queen has two magic tours 2×4, that are alternative numberings of the same closed tour.

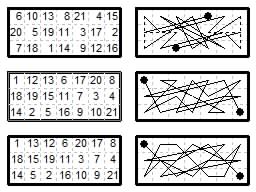
In Chessics #26 (1986) I reported finding 39 basic magic numberings for the 3×5 board. These occur in 19 pairs that are reversals of each other, and one which is its own reversal. This special case allows for four symmetric magic tours. Two of these use four move types, DFNC or DFNZ. The magic constants are 24 and 40. The moves used are: {1,3}{1,2}{1,1}{0,2} and {2,3}{1,2}{1,1}{0,2}. This work was anticipated by Charles Planck who mentions the figure of 39 solutions, and gives one magic tour using six move types in Andrews (1917, Fig.454).
The other two diagrams above use six move types plus the {0,4} closure move.
Left moves used: {1,4}{1,3}{1,2}{1,1}{0,1}{0,2} and {0,4}.
Right using Zebra instead of Camel. Moves used: {1,4}{2,3}{1,2}{1,1}{0,1}{0,2} and {0,4}.
Magic tours adding to 33 in files, 77 in ranks.
(a) Symmetric magic tours.
(1) Five move types. {1,4}{2,3}{1,2}{1,1}{0,2} plus{2,2} closure.
Unlike other examples this is without wazir moves.
(2) Five move types. {1,4}{1,2}{1,1}{2,2}{0,1} plus {2,6} closure.
This uses the same magic files as an asymmetric example by Trenkler (1999)
but reduces the number of types of move from 9 to 6 counting the closure move.
(3) Six move types {1,5}{1,2}{1,1}{2,2}{0,1}{0,2} plus {2,6} closure.
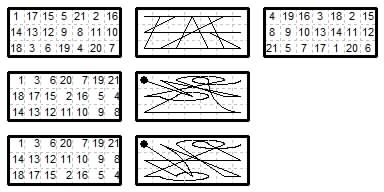
(b) Asymmetric magic tours.
(1) Five move types {1,3}{1,2}{1,1}{2,2}{0,1} or WFNAC. A closed tour..
(2) Five move types {1,2}{2,4}{1,1}{0,1}{0,2} plus {0,6} between end points.
(3) Five move types {2,3}{1,2}{1,1}{0,1}{0,2} plus {0,4} between end points.
(4) Five move types {1,4}{1,3}{1,2}{1,1}{0,1} plus {2,2} between end points.

(c) Asymmetric magic tours with an arithmetic progression (AP) 8-14 in one rank.
These are difficult to show graphically because of the multiple overlapping rook moves.
(1) Seven move types {1,2}{2,4}{0,1}{0,2}{0,3}{0,4}{0,5}.
This can be described as a Raven (Rook+Nightrider) tour.
It has a permuted AP in the middle rank. This was published in my online Jeepyjay Diary 13 Oct 2014.
The reverse numbering shown on the right, oriented by the Frénicle rule, looks very different.
The {0,4} closure move is also used internally, so this can be described as a closed tour.
(2) Seven move types {1,5}{1,3}{1,2}{2,2}{0,1}{0,2}{0,3} plus {0,6} closure.
This tour has the AP in sequence in the bottom rank. This is from Pickover (p.146) but rotated.
(3) Seven move types {2,5}{2,3}{1,2}{2,2}{0,1}{0,2}{0,3} plus {0,6} closure.
This tour has the AP in the middle rank. It is related to the tour from Pickover
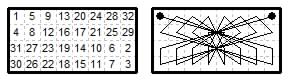
Symmetric magic tours, files add to 42 ranks add to 126.
(1) Five move types {1,6}{1,3}{1,2}{1,1}{0,2} Closed tour by M. Trenkler (1999) based on three 3×3 magic squares.
(2) Six move types {2,3}{1,2}{1,1}{0,1}{0,2}{0,5} A permutation of the files of the Trenkler tour.
(3) Six move types {1,4}{1,2}{1,1}{0,1}{0,2}{0,5}. Another permute of the Trenkler tour:

4×6 board. Bison+Knight with {3,3} closure, by E. Huber Stockar (1935).

4×6. Magic tour (Jelliss) with four move types plus {0,3} end separation, derived from a king tour. Filesum 50. Ranksum 75.
This with 1-2 and 3-4 ranks transposed has 5 move types. Other permutes have 5 or 6 types.

Magic rectangle by L. S. Frierson [Andrews Fig.271 reflected]. Adds to 66 & 132. Closure move {0,7}.
Symmetric magic tours. The magic constants are 90 and 126 (i.e. 5×18 and 7×18)
(1) Six move types {1,4}{1,3}{1,2}{1,1}{0,1}{0,2} plus {4,6} end separation. Composed by me on 12 June 2016 (our Queen's official 90th birthday) and is the best so far found on this board. This was derived in part from the arithmic king tour on this board, but also used the method of complementary differences by Charles Planck, as described in Andrews (1917, p.257-262). The example by Planck shown there uses ten move types.
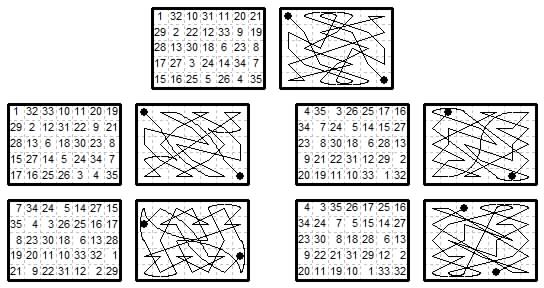
The other four tours (Jelliss 13 June 2016) are all permutes of the first, with the same numbers in the ranks and files.
(2) Seven move types {1,4}{2,3}{1,2}{1,1}{3,3}{0,1}{0,2} with {4,6} end separation.
(3) Seven move types {3,4}{1,3}{1,2}{1,1}{2,2}{0,1}{0,2} plus {4,4} end separation..
(4) Seven move types {1,3}{1,2}{2,4}{1,1}{3,3}{0,1}{0,2} with {2,6} end separation.
(5) Eight move types {3,5}{1,4}{1,3}{1,2}{2,4}{1,1}{0,1}{0,2}. Reentrant tour.
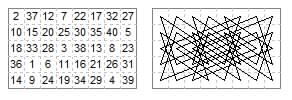
5×8. E. Huber-Stockar (Fairy Chess Review, vol.5, Feb 1943 p.28 and Apr 1943 p.37, prob 5447). A symmetric closed tour moves in four given directions. Bergholtian type since b2-g4 and c4-f2 cross at the centre point. Renumbered from b2 to g4 so that diametrally opposite pairs all add to 41 (in the source the tour was numbered a5 to d3, giving two different diametral sums 5 and 45).
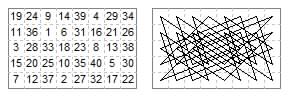
5×8. E. Huber-Stockar (FCR April-June 1943 problem 5500). Symmetric closed 5×8 tour by this mover, in four given directions. The original numbering is retained. The symmetry is Bergholtian and the diametrally opposite numbers add to 41.
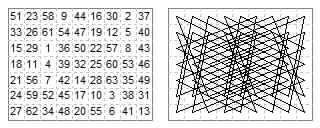
Symmetric magic tour. The magic sums are 254 (7×32) and 288 (9×32).
Ten move types {2,5}{3,4}{1,4}{2,3}{2,6}{1,2}{11}{2,2}{3,3}{0,1} and {6,8} end separation.
This is the best I have found on the 7×9 board (Jeepyjay Diary 18 Dec 2014) derived from a King tour.
Some of the diagonal moves overlap.

7×9. E. Huber-Stockar (FCR Apr 1944 p.85 and Jun 1944 p.94, prob 5935).
Symmetric open or closed tour with moves in four given directions. The centre cell has the middle number 32, and diametrally opposite pairs add to 64. The {2,4} closure move 1-63 passes over the centre cell, the moves through the centre 31-32-33 overlapping in the same line.
7×9. E. Huber-Stockar (FCR Aug 1943 p.53 and Oct 1943 p.63 prob 5659). Closed symmetric tour 7×9 with four types of move in four directions.

In the original numbering (shown on the right) the centre cell is 63 and diametrally opposite pairs add to 63. I prefer the numbering on the left where the middle number 32 is in the centre and the 1-63 move passes over the centre. In this diametrally opposite numbers add to 64.
8×12. E. Huber-Stockar (FCR Apr 1945 p.132 and Jun 1945 p.142, prob 6380). Moves in four given directions. The diagram shows the moves 1-48 of the first half of the tour, and the middle {3,5} move 48-49 in bold which passes through the central point (as does the closure {3,7} move 96-1). The other half is diametrally related to the first half. Diametrally opposite nmbers add to 97.
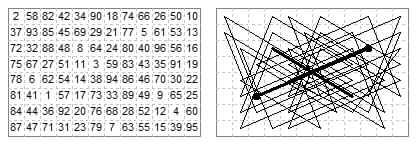
8×12. This is our only example of a Quadruple Beast. Tour on 8×12 with moves in four directions. E. Huber-Stockar (FCR vol.5 Dec 1944 p,117 and Feb 1945 p.126, prob 6229).
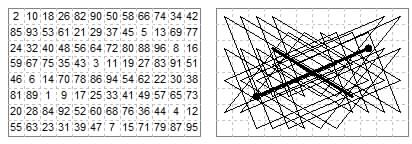
Half tour shown and cross-centre links 48-49 and 96-1. The rank sums are 612, 576, 540, 600, 564, 624, 588, 552 which form an arithmetic progression (cd 12). The rank constant is 582. The file sums are 404, 388, 468, 404, 388, 372, 404, 388, 372, 308, 388 372 (file constant 388). The numbers 308, 372, 388, 404, 468 have differences 64, 16, 16, 64.
There is a large tour 11×23 of four moves {1,4} {3,5} {3,8} {2,9} in Huber Stockar's original paper (1935), but too large to reproduce adequately here.