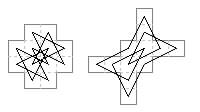
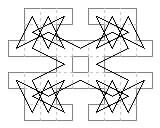
Here we gather examples of biaxial symmetry, also known as 'direct quaternary symmetry'. This type of symmetry is impossible in knight tours of rectangular boards. Consequently it is less familiar than the birotary type and its study has been neglected. It requires shaped boards having nonrectangular outlines or with holes, or both. The axes can be diagonal or lateral.
This web-page has been completely recast (June 2022) to conform to the PDF version issued in 2019, and to group the tours in three classes according to structure. It includes a number of new results. Particular attention is drawn to the one by Andrew Usher (see the diagonal entry for 44 cells).
The axes of the tour must either have two cells through which the tour passes (Murraian type) or have moves crossing the axis in pairs (Sulian type). One axis however is always of Murraian type. The second axis can be Murraian or Sulian. Thus, as for the Axial tours, there are three types of symmetry: Doubly Murraian type, (1) Diagonal or (2) Lateral, and (3) Suli-Murraian type. The Sulian axis is necessarilty lateral, since a diagonal Sulian axis requires a loosely connected board which is excluded from our study. The tours in the first two classes are all Eulerian (circling the centre), while the Suli-Murraian tours are all Bergholtian (passing through the centre).
12 cells. These two tours also appear in the section on Smallest Tourable Boards.
They are by Euler (1759) and Jelliss (1995).

For biaxial symmetry where the axes are diagonal the tour must enter only two cells on each diagonal. If there are to be no holes in the board then the diagonal cells used must be adjacent and the other cells of the board must grow cross-like from this central 2×2 hub. See the entries of 20 and 44 cells for other examples of this type.
16 cells. Four tours showing biaxial symmetry with diagonal axes on two board shapes with holes. The second diagram is among H. J. R. Murray's notes (c.1942).
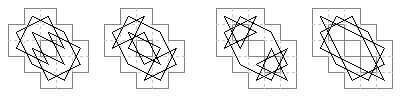
20 cells. The first, on a Greek cross (Euler 1759) and the second, with a 2×2 hole (Jelliss 2013).
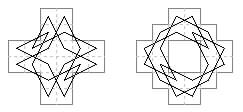
24 cells. Examples with diagonal axes (Jelliss 2017). In the second example the pairs of moves at c3 and e5 can be 'folded out' to f6 and b2 respectively, leaving holes at c3 and e5 though the board is still connected. This case is now given its own diagram. Also shown is an alternative tour on the same single-hole board (Jelliss 2022).
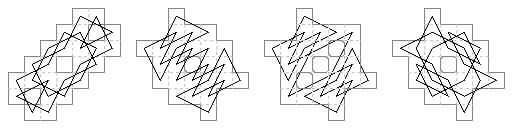
28 cells. Four tours with holes showing diagonal biaxial symmetry. All these boards have the same outline but different hole placements. The last two here are in Murray's notes (1942).

32 cells. Example with three holes, Jelliss 2022.
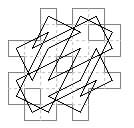
36 cells. Biaxial symmetry on an octonary board (Jelliss 2022).
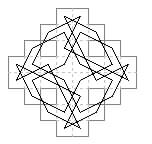
40 cells. The first diagram here (Jelliss 2017) gives rise to three new tours, still on connected boards, by 'folding out' of various pairs of moves, such as .d2-c5-e4 or g4-f2-h3, and their similarly placed reflections in the other quarters. The fourth example combines both these transformations.
See 48 cells for another quartet of tours related in this way.
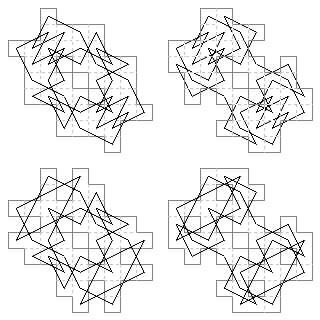
44 cells. Biaxial with diagonal axes and no holes (Jelliss 1999). (See earlier for two of 12 and one of 20 cells). The tour in the 8×8 frame with corners and cenntral 4×4 removed is by Andrew Usher (2022). It is similar in structure to the first 28 cell tour in the 6×6 frame.
.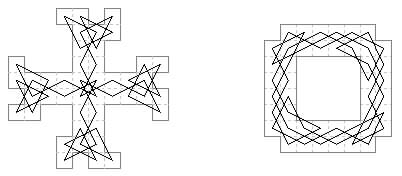
48 cells. In the first diagram (Jelliss 2017) it was noted that the pairs of moves on c4, d3, f7, g6 could be folded out to b1, a2, g9, h8 to leave two three-cell holes, and a new pair of single cell holes at b2, g8, though the board remains connected. This is now illustrated in the second diagram. The same process can be applied at the other corners, and at both corners together, giving the other patterns shown
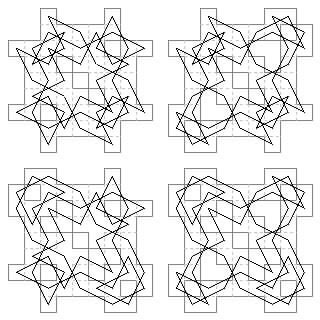
52 cells. Direct quaternary symmetry. Diagonal type from H. J. R. Murray's unpublished notes (1942).
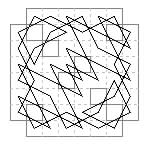
16 cells. The omission of this case from earlier accounts has been pointed out by Andrew Usher. It is part of a series of 3-rank constructions, this one having a single central hole.
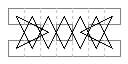
When both sides of the containing rectangle are odd there is necessarily a central hole. Biaxial tours of 4·m cells with lateral axes are then feasible, the four quarter-paths each joining a cell on the vertical median to a cell on the horizontal median, these being the only cells on the medians that are used. (The Octonary 3×3 star and 5×5 'bound cross' are special cases of this.)
20 cells. This tour (Jelliss 2017) with cross-shaped hole is within a 5×7 frame.
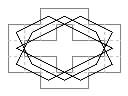
24 cells. Example with lateral axes (Jelliss 2017). In this the cells at d3, f3 can be moved to b3, h3, leaving a 5-cell hole, as now shown in the second diagram.
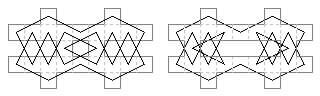
28 cells. Four seven-cell paths (Jelliss 2022).
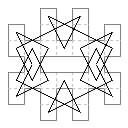
32 cells. Two more examples. (I'm not sure if the first is my own or from Murray.) The second is similar to a 30-cell Suli-Murraian example formed by omitting the two cells on the vertical axis and closing up, leaving a four-cell hole, which changes the symmetry from Eulerian, as here, to Bergholtian.
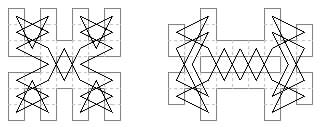
36 cells. Doubly Murraian. This may also be from Murray.
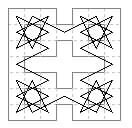
40 cells. Tour in a 7×9 area (Jelliss 2017).
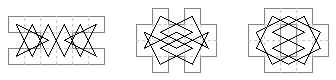
44 cells. Four eleven-cell paths (Jelliss 2022).

48 cells. Tour in a 9×9 area (Jelliss 2017).

52 cells. Tour (Jelliss) with both sides odd 7×9.

It is easy to fall into the error of supposing that a tour with quaternary symmetry can only be possible on a board with a multiple of 4 cells, since it seems obvious that each quarter of the tour must have the same number of moves, m. This is true in the case of biaxial symmetry with diagonal axes, however with lateral axes a tour may be possible using 4·m + 2 cells instead of 4·m. This is because of the possibility of Bergholtian symmetry, in which the path crosses itself at the centre of the board, so that each of the two central moves contributes half a move to each quarter, thus making the total 4·m + 2 possible. The containing rectangle from which the board is cut must be odd by even. Such tours are in the form of a convoluted figure-of-eight or infinity sign. The mid-point of each loop of the 'eight' must be in a cell on the middle line of the odd side, and there can be no other cells on this axis, so the board is of 'dumbbell' or 'hour-glass' shape. Apart from the 10-cell tour this type of symmetry does not seem to have been noticed before my study of the subject. All tours of this type with up to 50 cells and omitting cells only in the middle file are included in this collection.
10 cells. This tour by O. E. Vinje (1949) as part of hia enumeration of 10-cell tours also appears in the section on Smallest Tourable Boards. It was known to Murray earlier.

14 cells. Three tours with lateral biaxial symmetry similar to the 10-cell case.
18 cells. More tours with lateral biaxial symmetry (Jelliss 2016). One board has two solutions.
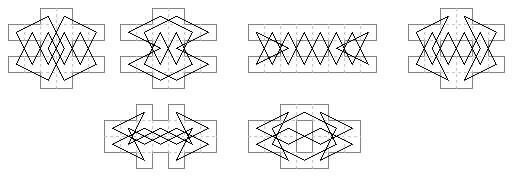
22 cells. More lateral biaxial symmetry (Jelliss 2016).
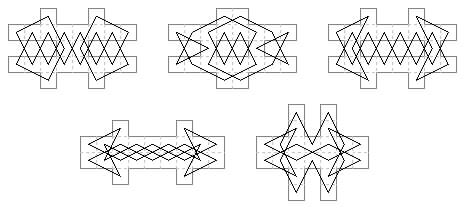
26 cells. Biaxial symmetry, with lateral axes, on assorted board shapes.
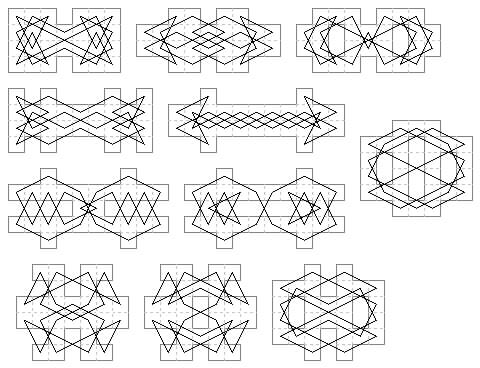
30 cells. More Suli-Murraian biaxial symmetry.

34 cells. Biaxial lateral. The 'dumbbell' shape has three tours.
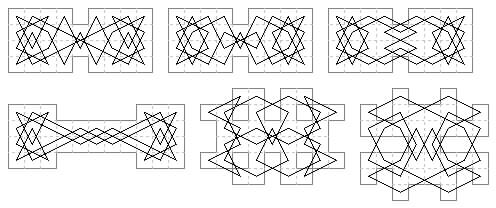
38 cells. Two more Suli-Murraian tours.
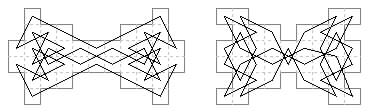
42 cells. Biaxial, lateral type. There are five tours on the dumbbell board.
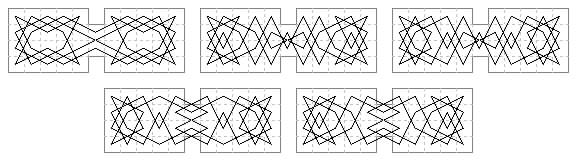
other assorted shapes:
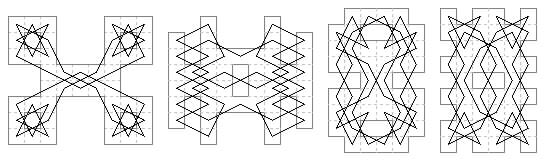
46 cells. Biaxial with lateral axes, Suli-Murraian.
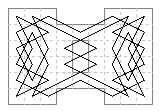
50 cells. This is the largest size of board on which I have constructed tours of the dumbbell type with biaxial lateral symmetry. (See also 10, 14, 26, 34, 42). Three differently proportioned dumbbells are possible: 7×8 (5 solutions), 9×6 (23 solutions), 13×4 (9 solutions).
A. 7×8 case: 5 tours. In the striking first tour the knight's moves are all within the boundary.
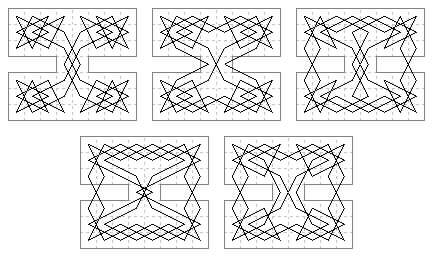
B. 9×6 case: (a) 6 tours with straight cross-centre moves.
Only the first is contained within the border.
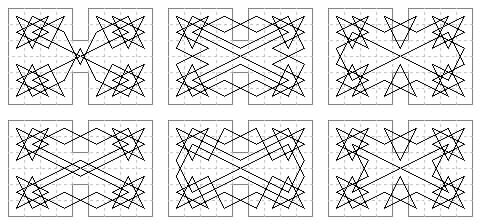
B. 9×6 case: (b) 9 tours with obtuse angled cross-centre moves.
The first two are within the border.
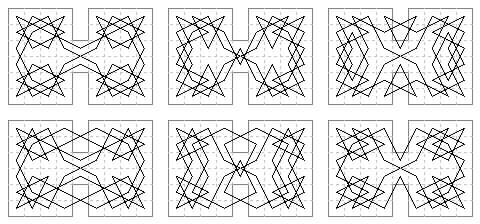
continued:
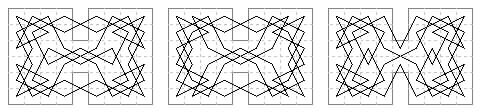
B. 9×6 case: (c) 8 tours with right or acute angled cross-centre moves.
The first one is within the border.
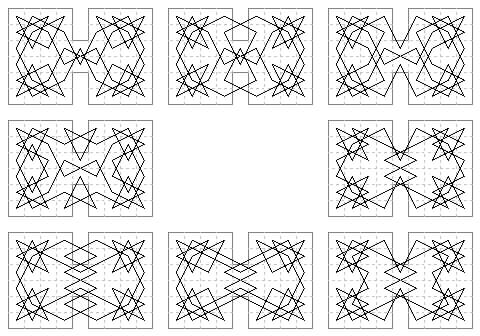
C. 13×4 case: 9 tours. Six are within the border.
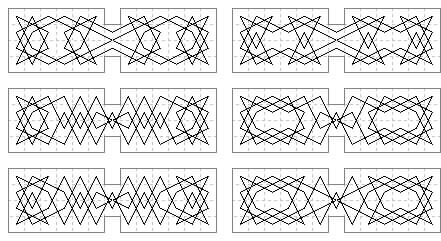
and three others:
