
To make space for the new enumerations by Andrew Usher of 11 cell open symmetric tours and 14 cell closed symmetric tours I have decided to expand the page on Smallest Knight-Tourable Boards to cover two pages - Part 1 Open Tours and Part 2 Closed Tours. These cover tours of up to 15 cells. Open tours have been completely enumerated, including asymmetric cases, only up to 9 cells. Examples of tours on larger boards of 16 or more cells are shown on separate pages classified according to the symmetry they show. In open tours the symmetry is necessarily binary, that is with a single axis of symmetry or with 180° rotation. Boards with an odd number of cells of course only admit open tours.
The smallest knight-tourable boards are the two 7-cell boards shown below, each of which is tourable by both wazir and knight uniquely. The tours have the same symmetry as the boards, namely axial symmetry, lateral or diagonal. The U-shaped case appeared in the earliest Arabian chess manuscripts (al-'Adli, c.840) in the form of a puzzle where you are to place seven pawns round three edges of the 3×3 board, leaving only the top square vacant, each new pawn being placed at a knight's move from the preceding one (Murray 1913 p.337). The trick is to start at a knight's move from the vacant cell.

There are 10 boards of 8 cells (octominoes) that are knight-tourable, with open tours.
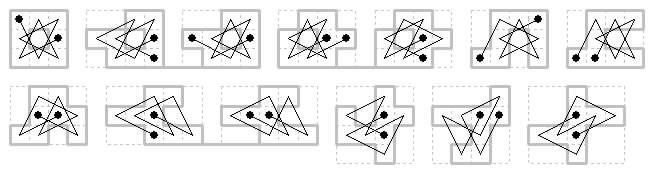
Only the centreless 3×3 board admits a reentrant or closed tour. Within the 3×4 frame there are three shaped boards each with a single open tour, and two holey boards, each with two open tours. In the 3×5 frame there is one shaped board that can be toured in two ways. In the 4×4 frame there are two shaped boards each with one tour. In the 4×5 frame there is one tourable board with one tour, this is centrosymmetric.
The collages below show the open tours of 8-cell boards joined to form a single open tour. The first, excluding the 3×3 case, fits them within an 11×11 area, the second, including the 3×3 case, takes a 10×13 board. These include the symmetric case.
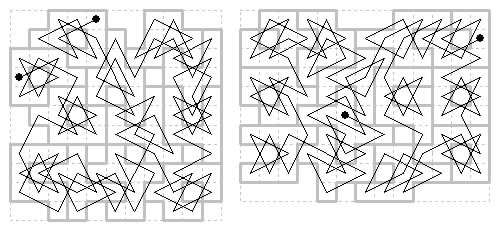
The latest check (17 July 2013) on my enumeration of the 9-cell tours finds 56 tourable boards with 93 tours. Here are diagrams of the 10 symmetric tours (2 oblique, 8 direct). One in the 3×4 frame, axial. Four within the 3×5 frame, two oblique, two direct. Two holey boards within the 4×4 frame, each with two tours, with diagonal axis (they also have asymmetric tours). Finally one within the 5×5 frame also with diagonal axis.

The two boards within the 4×4 frame above also each have two asymmetric tours, shown below. There are also two other symmetric boards, 3×4 and 3×5, that each have three asymmetric tours, but none symmetric:

Here are drawings of the tourable asymmetric boards within the 3×4 and 3×5 frames.

Here are diagrams of the tourable asymmetric boards within the 4×4 frame. There is one board that can be toured in 6 ways. Besides the two symmetric boards shown above, another asymmetric board can also be toured in 4 ways. There is also one that tours in 3 ways. These are all of holey type.

There are seven in the 4×4 that tour in 2 ways, and the remaining 13 uniquely.

Within the 4×5 frame there is one board with three tours, and three with two tours and seven with single tours.

On 10 cells there are 9 centro-symmetric open tours (using 6 shapes of board). Note that one of these tours is reentrant (derived from the 10-cell Bergholtian closed tour). See Part 2 for the 12 closed tours.
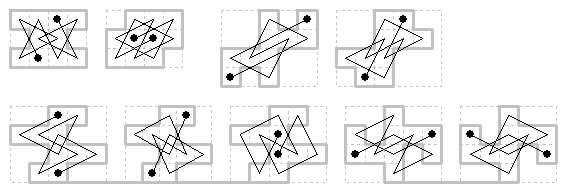
Andrew Usher has found that there are 37 distinct symmetric open tours on 11 cells (previously we showed diagrams of only 12).
3×5 frame with 4 cells omitted. Three board shapes.
Four rotary tours. Two lateral axial tours, one with long axis and one with short axis.
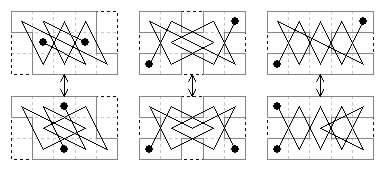
4×4 frame with 5 cells omitted. Two board shapes.
Eight diagonal axial tours.
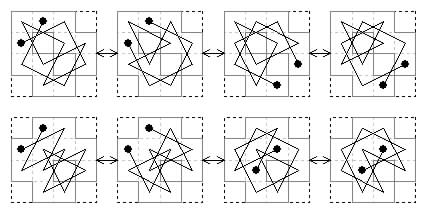
4×5 frame with 9 cells omitted. Two board shapes.
Three lateral axial tours.
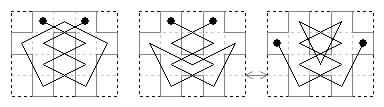
5×5 frame with 14 cells omitted. Ten board shapes.
Four rotary tours on two board shapes. Fifteen diagonal axial tours on eight board shapes.
Here are the rotary tours.
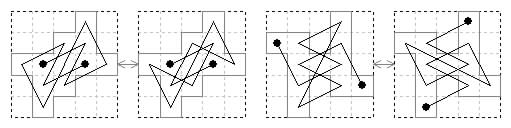
There are two board shapes, each with three diagonal tours.

There are three board shapes each with two diagonal tours.
And three board shapes with a single diagonal tour.

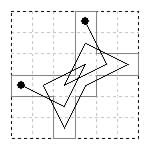
6×6 frame with 25 cells omitted. One board.
One diagonal axial tour.
Total of tours = 37.
The 11-cell asymmetric open tours have not been enumerated.
Here we encounter the first examples of tours of rectangular boards, namely the three tours of the 3×4 board which were found by Euler, two of which are symmetric (we also diagram the asymmetric tour). There are two other three-rank symmetric open tours, within the 3×6 frame. It may be noted that these two tours can be joined, jigsaw-style, to copies of themselves to form open tours within frames 3×10, 3×14, 3×18, and so on endlessly.

In all there are 49 geometrically distinct 12-cell symmetric open tours. These consist of: 2 rectangular (3×4 board), 12 reentrant (derived from the 6 bergholtian tours above by deleting one of the central moves), 27 other shaped-board tours, and 8 with holes. The 27 shaped-board tours use 18 shapes of board. The next diagram shows the 10 shaped boards within the 4×5 frame (1 with 3 tours, 5 with 2 tours, 4 with 1 tour).

Next we show the tours within the 4×7 frame (1 tour), and 5×6 frame (2 with 2 tours, 3 with 1 tour):

There are also eight 12-cell centrosymmetric open tours with holes. Of these 7 are on the same board with two single-cell holes, and 1 is on a board with a two-cell hole.

12-cell asymmetric open tours have not been counted. There is the one on the 3×4 board diagrammed above. There is only one closed tour within the 3×5 frame, and it is asymmetric, so produces 12 reentrant tours. In a partial enumeration not yet checked, I found 39 non-reentrant tours within this frame. These tours use 10 different board shapes. Removing the minority color square from a2 the other two cells removed can be a1, b2; a1, c3; a1, d2; a1, e1; a1, e3; b2, e1; d2, e1; e1, e3; and with b1 as the minority cell, the others are a3, d2 or a3, e1.
By omitting two cells from the untourable 3×5 board two centrosymmetric tours are possible, and also eight asymmetric tours, two on each of four symmetric boards (one of which has a hole). There are also two asymmetric board shapes, each tourable in eight ways.

The four diagrams below, of asymmetric open tours, solve the problem of a maximum length open knight path on the 3×5, by omitting one cell, which has to be a corner cell.

No complete tour is possible on the 4×4 board. The diagrams shown here solve the problem of a maximum length open knight path on this board. There are 20 distinct 15-cell open paths on the 4×4 board, omitting one corner cell. They all have at least one end in a corner (there are in fact 24 directed tours from a given corner since the 4 corner-to-corner cases can be reflected in the diagonal through the missing cell).
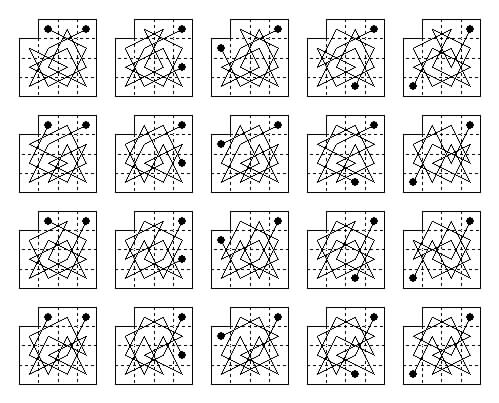
They are classified here according to the five end-positions.