The modern study of the knight's problem appears to have begun in the 18th century without knowledge of the mediaeval work, save perhaps for the half-board tour in Guarini's work. The subject first reappeared in Jacques Ozanam's Récréations Mathématiques et Physiques, which was a compilation in the tradition of C. G. Bachet's Problèmes Plaisans et Délectables which first appeared in 1612, and was imitated in numerous other collections of puzzles, tricks, mathematical recreations and popular scientific effects for entertainment and instruction at social gatherings. The first edition of Ozanam's work was published in 1694 but (according to one of the later editors, C. Hutton) Ozanam died in 1717.
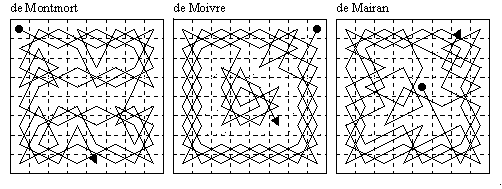
The first edition of Ozanam's work to contain the knight's tours by the mathematicians Raimond de Montmort, Abraham de Moivre and Jean-Jacques de Mairan was that published in four volumes in Paris by Claude Jombert in 1725 (vol.1, pp.260-9). Ozanam's compilation appeared in numerous revised and translated editions, under various editors and publishers until the mid 19th century (for details see the Bibliography).

The tours were supplied to the editor of that edition of Ozanam in 1722 by de Mairan, who was Director of the Académie Royale des Sciences, Paris. This date is printed in the margin of the book. Rouse Ball (1939) says the tours by de Montmort and de Moivre “were sent by their authors to Brook Taylor who seems to have previously suggested the problem”; unfortunately he gives no reference to where he learnt of the involvement of Taylor (another well known mathematician) and I have been unable to verify this. Similarly Kraitchik attaches the date 1708 to the de Montmort tour, but it does not appear in de Montmort's famous work l'Essai d'analyse sur les jeux de hasard, Paris 1708. A slight variation of the de Moivre tour in which the last three moves are reflected is mentioned in the text and is sometimes diagrammed in later accounts.
It is evident that these tours do not reach the same degree of development as was achieved by Suli 800 years earlier. All are open tours. The de Moivre tour is on the same plan as the Mani tour in that it starts in a corner and skirts the edges of the board, as far as possible, before filling the centre. The de Montmort tour is similar to the al-Amuli tour and earlier tours formed by connecting half-board tours.
The first mathematical paper analysing knight's tours was presented by the most productive mathematician of the eighteenth century, Leonhard Euler (1707–1783), to the Academy of Sciences at Berlin in 1759 (but not printed until 1766). This paper has been of considerable influence, the starting point (but often alas the end also) of many later accounts of the subject. Euler had been working on the topic for several years, since he gave a symmetric tour in a letter to C. Goldbach in 1757. Kraitchik (1927) says that the Academy of Sciences of Berlin proposed in 1759 a prize of 4000 francs for the best memoir on the problem of the knight, but that the prize was never awarded. Since Euler was at that time Director of Mathematics at the Berlin Academy (resigning in 1766 in favour of Lagrange) he was presumably ineligible for the prize or would surely have won it. Although published in Berlin the paper is written in French, with the title: “Solution d'une question curieuse qui ne paroit soumise à aucune analyse” {Solution of a curious qestion which does not seem to have been subject to any analysis}, Mémoires de l'Academie Royale des Sciences et Belles Lettres, Année 1759, vol.15, pp.310–337, Berlin 1766.
A downloadable PDF of this paper is available at the Euler Archive, linked here:
Euler Works
It has the index number E309. My account below is based on a photocopy supplied some years ago by the British Library.
He begins: §1: “I found myself one day in company where, on the occasion of a game of chess, someone proposed this question: to traverse with a knight all the cells of the chessboard, without ever arriving twice at the same, and commencing from a given cell.” He describes how the course of the knight was followed by placing counters on the cells and removing them one at a time as the cells were visited by the knight. In §2-4 he gives an example open tour shown, in the same way as in Ozanam, by numbering the successive cells occupied by the knight on an unchequered diagram, and notes that the numbering of any tour can be reversed. (We show the tour in graphical form below.)
§5: Acknowledges that he has been guided in his researches by an idea furnished by Monsieur Bertrand of Geneva. Bertrand (1778) apparently also subsequently issued an account of it. The general rule Euler describes is simply to make repeated application of what Murray (1942) calls the 'Bertrand Transformation'. This means locating a sequence of cells connected by knight moves, and numbered, say a...y, in which an end cell, y, is a knight move from an internal cell, say e; it can then be renumbered in the sequence a...ey...f. If an unused cell z (or the end of another sequence of moves z...) is a knight move from f then z... can be incorporated into a...y by a...ey...fz.... Geometrically the move ef is deleted and the two moves ey and fz inserted. For example, in the first open tour, numbered 1...64, cell 50 is a knight's move from cell 64 and 51 is a knight's move from cell 1. This enables it to be converted to a reentrant tour 1...51.64...52 as shown in the second diagram. Using the same numbering, the third diagram has the formula 1...11.32...41.12...31.64...42.
In §6-8 he gives a diagram of a closed tour derived from the open tour (by deleting d2-b3 and joining the loose ends b1-d2, b3-a1). Euler indicates that this solves the stated problem of making a tour from any given cell; in fact that it provides two ways of doing it, since the circuit can be described in either direction (second diagram below). In §9 he indicates that he will explain a sure method by means of which one can “discover as many satisfactory routes as one might wish: for though the number of these routes may not be infinite, it will always be so large that one would never exhaust them.” He distinguishes 'simple' (i.e. open) and 'rentrante' (i.e. closed) tours. In §10-14 he derives a series of 17 further tours from the initial two by applying his method. All of these are very similar, five are closed; we show a corner-to corner example and one other. This is the only open tour he gives that does not have one end on an edge cell, so he did not attempt the task of constructing a tour between all possible pairs of cells, though his method could be used for that purpose. In §15-23 Euler derives 35 further irregular tours by this method from another randomly constructed partial tour, all again very similar to the initial try; four are closed. I show only two from this series.
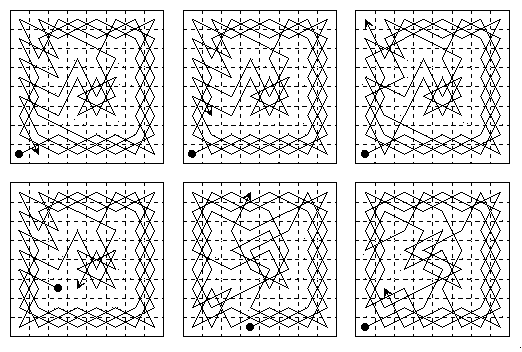
In §24-30 having explained a way of finding many tours he goes on to consider tours of special types using the same method. First he constructs symmetric tours, invariant to 180° rotation, which he forms by constructing two diametrally opposite paths simultaneously, joining in any unused cells and then arranging for the end of each path to be a knight's move from the start of the other. Five tours result, all of which are shown here. Apart possibly from the Nilakant-ha tour, whose date is uncertain, these are the first fully symmetric tours composed.

Euler is the first to point out that when a tour is presented in numerical form symmetry on the 8×8 board is characterised by the property that the numbers in diametrally opposite cells have the constant difference of 32.
§31-34: Next he turns to symmetric tours composed of two equal 4×8 half-board tours, also constructed by the same methods as before, and presents five examples, all shown here.

In the concluding sections of his paper Euler turns to tours on smaller boards, which apart from the 4×8 board which was popular in mediaeval times, seem not to have been considered before. We give diagrams of all these tours in other sections of these Knight's Tour Notes.
§35: He notes that no tours are possible on squares of 4, 9 or 16 cells, but in the latter case gives a 15-cell open path, omitting a corner cell.
§36-40: He notes that, since odd and even numbered cells follow alternately, a reentrant tour is not possible on any board with an odd number of cells, since the numbers on the first and last cells in the tour are odd. On the 25-cell board he notes that every tour must commence or finish at a corner cell. He diagrams one corner-to-centre tour and gives formulae for 34 others, including all eight symmetric cases (all corner-to-corner type), which are also given separate diagrams.
§41: He then joins together four copies of a 25-cell tour to make a 100-cell square tour. This is the first ever example of a tour with quaternary symmetry.
§42-44: On 3-rank boards he gives the three possible tours on the 3×4 board (four in numerical form), notes that no tours are possible 3×5 or 3×6, and gives two examples 3×7. On other boards he gives single examples 4×5, 4×6, 4×7, 5×6 and 6×6, and concludes with four tours on cross-shaped boards, two of which show quaternary symmetry with diagonal axes, a type of symmetry not possible in tours of rectangular boards.
Unfortunately, in §42 Euler stated incorrectly that closed tours are not possible on boards with side less than five cells, and his influence was so great that no one seems to have questioned his statement for 150 years! For instance Ahrens (1910, p.350) repeats the assertion. Ernest Bergholt showed the error in 1917 by constructing closed tours 3×10 and 3×12.
The first book to show knight's tours in the form of line diagrams instead of in numerical form is a beautifully printed book, Corsa del Cavallo per tutt'i schacchi dello Scacchiere, printed by dalla Volpe at Bologna. The style of diagram is very similar to the form we use here except that the border is shown as a doubled line, with finer lines dividing the board into squares.

The heading on p. 3: “Lo Stampatore a chi si diletta Del Giuoco de1 Scacchi” {The printer to those who delight in the game of chess} may indicate that dalla Volpe is the author as well as printer and publisher; perhaps he himself made the blocks for printing the elegant diagrams. His frontispiece is of especial interest since it shows a proper closed tour (i.e. no initial or final squares or direction of description are identified). His next ten diagrams, numbered I to X, show open tours commencing successively at the ten typical cells abcd8, bcd7, cd6, e5, thus solving the problem of showing an open tour commencing at any given cell. He does not distinguish the start from the finish point geometrically. The only source he cites is Ozanam, and his tour I is de Moivre's (variant form), reflected to start at a8 and end at f6. We show here tour III which incorporates a 14-cell path in the central 4×4, and tour IX in which the initial and final moves are unintersected.
Farkas Kempelen (1734–1804) of Hungary, also known as Wolfgang von Kempelen, achieved fame as inventor of the first chess-playing 'automaton', called the Turk, which was built in 1769, and was exhibited, with much publicity and popular interest, throughout Europe and America until 1854. This was not of course a true machine but was the first 'cabinet illusion', the cabinet supporting the figure being shown apparently empty, or occupied by machinery, but in fact concealing an operator. Besides playing chess with members of the public it was also able to demonstrate a knight's tour, from any square chosen by a spectator.
One frequent spectator, Karl Gottlieb von Windisch, in a letter dated 18/ix/1783, in a book he published that year (which appeared in English translation in 1819), describes how the knight's tour was exhibited. “The leap of the knight, which this machine makes traverse all over the board, is too remarkable not to be mentioned. It is this; as soon as all the chessmen are removed, one of the spectators places a knight on any one of the squares he thinks proper; the Automaton immediately takes it, and commencing from that square, and strictly observing the move of the knight, he makes it traverse the sixty-four squares of the chessboard, without missing one, and without touching any of them a second time; this is proved by the counter, which the spectator himself places on each square which the knight has touched, observing to put a white counter on the one from which he first begins and red counters on all those which he afterwards touches in succession. Try to do as much yourself with your chess-board, perhaps you will succeed better than I have done; all my attempts for that purpose have been unsuccessful.”
The Edinburgh Philosophical Journal 1821 reported: “The Automaton Chess Player of M[onsieur] de Kempelen was introduced into England by its inventor in 1783 and has during the last two years been exhibited in various parts of England and Scotland, under the direction of M[onsieur] Maelzel.” In the same year 1821 was published in London An Attempt to Analyze the Automaton Chess Player of Mr. De Kempelen. To which is added a copious collection of The Knight's Moves over the chessboard. No author's name is given but Tomlinson (1845) says the author of the section on the automaton was Robert Willis, later Professor of Mechanics at Cambridge. The text suggests that the tours section was written by the same author: "Observing that the Automaton, under the direction of Mr Maelzel, occasionally traversed half the board, I was induced to pursue the subject, and found that the move might be performed on any parallelogram consisting of twelve squares and upwards with the exception of fifteen and eighteen squares." He gives an open tour on each possible board up to 8×8 and closed tours 6×8, 7×8 and 8×8. His 3×4, 3×7 and 5×5 examples are the same as examples given by Euler. For diagrams see the sections on rectangular boards.
Johan Nepomuk Maelzel, inventor of the metronome, subsequently took the Turk to North America. After his death in 1838 a group of citizens from Philadelphia bought the machine and exhibited it until it was destroyed by fire in 1854. One of the group was Dr S. Weir Mitchell. To show a tour from any square it is of course sufficient to know one closed tour. A template for this purpose for use in the machine was presented by Dr Mitchell to the Chess Library of George Allen (1808–76) which was acquired by the Library Company of Philadelphia, in which collection it still apparently survives. It is 13 inches square, creased to be folded into quarters and pierced to be hung on a hook. Inside the Automaton it fitted over an array of 64 plugs on what I suppose can be called the operator's 'control board'. A photo of this artefact is in the Good Companion Chess Problem Club Folders (1917, p.140), it shows Euler's first closed tour.
The influence of the Automaton in promoting popular interest in the knight's tour was considerable; as much as reviews of Euler's paper over the same period in a wide range of publications.
The first author after Euler to make a significant original contribution to the subject, though he only gave the one 8×8 tour, was the mathematician Alexandre-Théophile Vandermonde, in an article on 'Problems of Situation' presented to the Paris Academy of Sciences in 1771, and published in their Mémoires in 1774. He begins by covering the board with four similar circuits which together form a pattern (which I call a pseudotour) with biaxial symmetry. He links opposite pairs of these circuits together, by deleting a pair of parallel moves and joining the loose ends, to give two congruent circuits each with diametral symmetry, which together still form a pseudotour having biaxial symmetry. Finally he links together these two circuits by the same method to form a true tour, which however does not preserve the symmetry. He presented the tour in the form of a geometrical diagram in which the squares of the board are omitted and the points where the knight moves meet are represented by small black and white circles.

Puzzle: Show how Vandermonde's four circuits can be linked to form a symmetric tour with only four deletions. This can be done in four ways.
Vandermonde was well ahead of his time in constructing a three-dimensional knight's tour of a 4×4×4
cube, in numbered-cell form it is:
63 12 25 34 26 41 54 13 05 62 33 18 42 17 04 55
28 35 64 15 59 16 29 46 38 21 08 51 07 56 43 20
39 24 11 52 06 53 40 19 27 48 61 14 60 03 32 47
10 49 36 23 37 30 01 50 58 09 22 45 31 44 57 02
Euler's paper (printed 1766) was reviewed in the Journal Encyclopédique, ii/1767, quoting his first two tours. Later that year Cosimo Alessandro Collini (1727 – 1806), who was at that time personal secretary to the Elector Palatine, submitted an article that appeared over three issues of the Journal Encyclopédique (ix–x/1772, pages 453–462, 112–118, 284–290) in which he explicitly stated (on page 285) the problem of finding a tour between given squares, and described a method of solution. The next year he published a more detailed account, in his book Solution du Problème du Cavalier au Jeu des Echecs (Mannheim, 1773). In the book his Part I prescribes the initial square, Part II the final square, Part III a closed tour, and Part IV different start and finish squares. In the journal only one tour is shown, on p.116, and the same tour is Table (5) in the book. The tours are given in tabular numerical form, but we show them graphically here.

Collini's method is to start from the pattern of eight circuits consisting of four 4-move circuits in the central area and four 12-move circuits in the surrounding border, seeking to join them up with minimal deletion of links. In the book he gives 20 tours ('Tables' 5, 7–9, 11, 13–21, 23–28). Of the 20 tours four are reentrant (11, 13, 15, 25). Only in one tour (20) does he connect two inner circuits in succession; the others all alternate outer and inner circuits. Of the 20 tours 12 use the minimal number of 8 deletions (and 7 insertions). To solve the problem when the start and finish squares are on the same circuit takes more than eight deletions, as in examples (14) and (15). The corner-to-corner tour (17) is one where he makes more deletions than necessary.
Puzzle: Construct a corner to corner Collinian tour using only 8 deletions.
In a letter from Prague dated April 1773, signed "Le Chevalier W., capitaine au régiment de Kinski", addressed to the editors of the Journal Encyclopédique and published by them in August 1773, pp.123-125, is the following tour. This was reproduced in later editions of Ozanam (see de Mairan 1722) and in many other sources since.
Writing from the East Indies, a Monsieur Monneron supplied two tours to the Nouveau Dictionaire, Pancoucke, Paris, 1776. The first of these is ascribed to a Malabarese (Malabar is in the south-west of the Indian subcontinent). The second is the Nilakant-ha tour (see the 1650 note in the Early History section). I have not seen the actual source, but both tours are quoted in Hoffmann (1893) who gives the first the heading 'Du Malabar' as if that was the name of its author.

The Journal Encyclopedique and the Nouveau Dictionaire were I think a continuation of the movement led by Denis Diderot (1713-1784) and Jean le Rond d'Alembert (1717-1783) whose great Encyclopédie appeared in many volumes over the years 1751-1772. Kraitchik (1927) states (in French): "According to the Encyclopedia of Diderot and d'Alembert the problem was known very long ago in India. The Brahmins, Hindu priests, already possessed, 2000 years ago, a procedure to resolve the question on the usual board". Unfortunately he does not give an exact reference for this (erroneous) statement, and I've not been able to trace it.
It is natural to try to devise some simple rule governing movement of the knight which would lead to the completion of a knight's tour. Such a rule would obviously provide another method of demonstrating the knight's tour as a conjuring trick. Most such rules however are only imprecise guides ('rules of thumb' or 'heuristics') and if applied strictly do not lead to completely determined tours, while those that do produce a complete tour tend to be difficult to apply and work only under very restricted circumstances. However, the resulting paths can be used as a basis for constructing a complete tour, say by Euler's method. The tours of Mani and de Moivre follow the approximate rule: 'Tour the border first as far as possible, and then the central area'. Collini's method can be regarded as an elaboration of this idea.
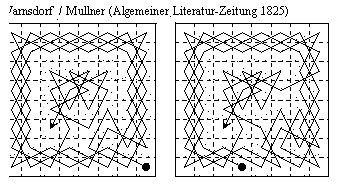
The most celebrated of these rules is that of H. C. von Warnsdorf, Des Rösselsprunges einfachste und allgemeinste Lösung {Knight's tours simple and general solution}, Schmalkalden (1823): “Play the knight to a square where it commands the fewest cells not yet used.” The tours shown above are given in a review of Warnsdorf's work (I have not seen the original). Strictly applied the rule falls far short of producing a completely determined tour. The best it gives, before it reaches a position where it is undecided on the next move is 18 moves, starting b3-c1. Nevertheless much has been written about this rule, and recently it has been the subject of computer studies. Warnsdorf claimed that when there is a choice of moves under the rule any of them can be taken, but examples can be given where this fails. The rule also involves a degree of backtracking, since you have to examine all possible choices of the next two moves to determine the next single move. Thus it may be claimed that it is not a proper tour-generating rule, in which all backtracking is prohibited.