
Sections on this page: — History of Figured Tours
— Figured Tours on Small Boards, including size 5 and 6 Square Boards
— Figured 7×7 Tours
— Figured 8×8 Tours with Random Numbers — Arithmetic Progressions
— Square Numbers — Other Sets of Numbers
— Figured Tours on Large Square Boards of sides 9, 10, 11 and 12.
— The Prime Queen and other Puzzles
"Studies in Figured Tours of Knight in Two and Higher Dimensions" by Awani Kumar PDF: Kumar 2021.
Dawsonian Tours (with the Squares in a Knight Path) are on a separate web page: Figured Tours - Part 2.
A tour presented in arithmetical form may include various numbers forming a pattern, making it a figured tour. Tours between given cells can be regarded trivially as figured since the end numbers (1 and 64 on the 8×8 board) are fixed, but usually we require more than this.
In retrospect figured tours showing arithmetic progressions can be seen in 3×4 and 5×5 tours by Leonhard Euler (1759). However the first deliberately composed figured tours are probably those given on the 8×8 board by Ernst von Sachsen-Gotha (1797). Similar examples are in H. C. von Warnsdorf (1823) but with fewer fixed points.
A special type of figured tour resulting from linking of four equal circuits occurs in Jaenisch (1862). The Harikrishna (1871) manuscript includes six figured tours by the Rajah of Mysore who originated the idea of having the specified numbers arranged in a knight wheel around the initial cell.
The problem set by G. E Carpenter and solved by S. Hertzsprung (1881) of arranging the square numbers along a rank was taken to be the origin of the subject by T. R. Dawson.
However, the main development of figured tours must be attributed to T. R. Dawson who first used the term and published a comprehensive collection of such tours, by himself and other contributors, in the Problemist Fairy Chess Supplement (1930-1936) and its continuation the Fairy Chess Review (1936-1958) of which he was founder-editor. This included a complete collection of 100 tours, which we now term 'Dawsonian', in which the square numbers delineate symmetric knight circuits. I must thank John Beasley for lending me (in November 1989) his complete set of these now rare magazines.
After some work by E. W. Bennett in Fairy Chess Review 1949-52 interest in the subject seems to have fallen away until I revived it in Chessics #5 1978, influenced by Anthony Dickins, beginning with a symmetric tour with the multiples of eight along a diagonal. This problem had been solved independently in asymmetric tours by Mysore and Dawson.
My next ventures in the subject appeared in Chessics #22 1985, including the Carpenter problem for the 6×6 board, and Chessics #25 1986, including a closed tour with the squares delineating a tour of the edges of a cube, and in an article in Mathematical Spectrum (vol.25 1992/3). This was followed by publication of my 22-page A4 booklet Figured Tours: A Mathematical Recreation 1997.
Diagrams of all the tours mentioned above are included below, classified according to the board size, the types of move used, and the choice of highlighted numbers. Dawsonian tours however, showing square numbers in knight chains, are shown on a separate page.
Leonhard Euler (1759) gave the tours on the 3×4 board. The top and bottom rows of the corner to corner tour form arithmetic progressions 1, 4, 7, 10 and 3, 6, 9, 12. These sequences also occur in the top row of the asymmetric tour, one in each of its two numberings.

A unique 16 cell tour on a shaped board solves a problem in my booklet on Figured Tours (1997): Find a 16-cell knight's tour, on a connected board, showing the first four square numbers 1, 4, 9, 16, forming a square. This can be regarded as a 4×4 board with three corner cells moved.

The board formed of the 3×5 with a cell added at the middle of each edge has no tours for the same reason as the 3×5 board: formation of a short circuit b2-d2-f2-d4 on the minority colour. However if the end cells are moved next to the side cells to form a board with rotary symmetry many tours become possible, in fact 62, made up of 16 b3-d3, 14 a2-e4, 14 a4-e2, 12 b5-d1, 6 c4-c2 (Jelliss Feb 2018).

In these the nine even numbers form a diagonal square, and in the six cases shown above this is a magic square! This research was stimulated by an 8×8 figured tour by T. R. Dawson (Vie Riennaise 1932) incorporating a magic square. (See further below).
Euler (1759) noted that in the symmetric tours opposite cells add to 26. It follows that the four lines through the centre add to the magic constant 65, though other lines do not. This is as near to a magic knight tour as can be achieved on this board. The first 5×5 symmetric tour in arithmetical form has the AP 1, 7, 13, 19, 25 along the diagonal and so is an example of a 'figured tour'.

These tours (Jelliss 2000) are a new type of figured tour in which four numbers 5-7-19-21 can be permuted but still form a knight tour!

Following my work on 'Wazir Tours with Squares in a Row' (Chessics vol.2 #21 Spring 1985 p.56, the unique result for the wazir on the 6×6 board naturally led me to look at the same problem for the knight on that board, and to find that there was again a unique tour.

This was in 'Notes on the Knight's Tour' (Special Issue of Chessics vol.2 #22 Summer 1985 p.61). The first diagram shows the only solution with the squares in order of magnitude.
Other solutions are possible with the squares in different sequence on the first rank. Three cases are shown, two having alternative routes. A tour with squares along the second or third rank is impossible. These results were reported in the booklet Figured Tours (1979).
It only recently occurred to me to try the Dawson problem of a tour with the square numbers in a closed knight circuit on the 6×6 board. For these see Figured Tours - Part 2.
My article on 'Figured Tours' in Mathematical Spectrum (1992/3) included a symmetric open tour 7×7 with arithmetical progression with c.d. 8 along a diagonal (analogous to the 5×5 with c.d. 6 shown by Euler).

Awani Kumar [September 2022] expands this section considerably by providing these 12 PNG images showing the seven square numbers 1, 4, 9, 16, 25, 36, 49 in various formations on the 7×7 board. The last two show the squares in five-leaper paths.

|

|

|

|

|

|

|

|

|

|

|

|
And an example with the multiples of 7 in a row.

The first deliberately composed figured tours are probably those given on the 8×8 board by Ernst von Sachsen-Gotha (Reichs-Anzeiger, 18 Sep 1797 p.366-368). He gives one with an arithmetic progression (see next section). At the end of the article is a diagram showing the numbers 1, 17, 24, 44, 64 on the cells d5, e4, e5, d4, f4, and in his library, which still exists, there is a manuscript with the title Auflösung einer systematische Aufgabe der sogennannter Roesselsprungs auf dem Schachbrete (dated 1798), which enumerates tours with the five numbers in these given positions, all naturally rather irregular.
I have however only seen an online image of the title page which shows 27 tours of this type. Why this choice of numbers is unclear. We show the first three:

Similar examples are in H. C. von Warnsdorf (1823) but with fewer fixed points. His Figs 74-83 show tours with 1 and 64 on given cells, the third number being 8, 24 or 36. Figs 84-91 specify the numbers 2, 18, 36, 64 on ranks 2, 4, 6, 8 in all possible files a-h.
A special type of figured tour resulting from linking of four equal circuits occurs in Jaenisch (1862) where the numbers 1, 16, 17, 32, 33, 48, 49, 64 mark the ends of the quarters. These normally form a knight circuit but can also appear in other formations, some of which are shown below. In the first tour they circle round the centre in alternating knight and wazir moves. This tour is demi-magic: four ranks and files add to 252 and the other four add to 268.

In the second tour the circuit alternates rook and knight moves and has a difference of 16 between numbers in diametrally opposite cells. The third tour is semi-magic adding to 260 in the files. Several magic tours have these Jaenischian properties.
Dawson Vie Riennaise 19 Nov 1932 The first nine even numbers forming a magic square (see above for my version of this on a 19-cell board).

An Arabic ms dated 1257, in the British Museum, contains two problems involving capture of pawns by a knight in minimum moves (H. J. R. Murray BCM 1902 p.1-7). The first has Ng1, Ps on a8-h1 diagonal, and is solved in 17 moves by the ingenious route shown.

The scheme of moves in the first diagram was rediscovered independently by D. E. Jackson (J. Rec Math 1993) in solving a problem posed by Eliot W. Collins of constructing a knight tour with minimum diagonal sum. The tour by Jackson counts as a Figured Tour since it has the first eight odd nmbers (1, 3, 5, 7, 9, 11, 13, 15) on the diagonal.
Two open tours by T. R. Dawson from the Congres International de Recreation Mathematique (CIRM) 1935 are shown. The AP with initial term 1 has 10 terms ending at 64. The first tour shows 9 of these terms in a square. The other shows multiples of 7 in a 3×3 array.

Two tours by S. H. Hall with APs with CD = 7. Closed tour (PFCS 1936 vol.2 #16 Feb 1936 p.172 ¶2178) and open tour (FCR vol.3 #13 Aug 1938 p.140 ¶3249) numbered 0 to 63.

The Rajah of Mysore's (Fig.67) in the Harikrishna manuscript (1871) has the multiples of eight along one diagonal in a closed tour. The same problem was solved independently by T. R. Dawson (CIRM 1935). In my example, Chessics #5 1978, the tour is symmetric.

The Rajah of Mysore appears to have originated the idea of having specified numbers arranged in a knight wheel around the initial cell. This example (Fig 35 in the Harikrishna ms) shows multiples of 8 on the wheel. My first tour shows a symmetric tour with an AP of CD 4 in a symmetric path of dabbaba (0,2) and fers (1,1) moves. My second tour has the octuples in a knotted octagon of (0,2) and (4,4) moves. From my 1997 Figured Tours booklet.

This tour (Dawson CIRM 1935) shows AP with CD = 9 along the fifth rank. The 9-move segments of this tour are alternately in the lower and upper ranks of the board.

The article by Ernst von Sachsen-Gotha (Reichs-Anzeiger, 18 Sep 1797 p.366-368) begins with a tour showing the multiples of 10 in sequence along a diagonal. The Harikrishna (1871) manuscript includes figured tours by the Rajah of Mysore (Fig. 62) with multiples of 5 or 10 on the diagonals and Fig 61 with multiples of 10 on the knight wheel round the initial cell.

E. W. Bennett in FCR 1949-52 constructed four tours showing arithmetic progressions with common difference 10 arranged along diagonals.

Three show two separate progressions.

This is from my article on 'Figured Tours' in Mathematical Spectrum (vol.25 1992/3 #1 p.16-20). Pairs of numbers aa, bb and ab, ba on adjacent cells and the central numbers 11, 22, 33, 44.

Tours with the Square Numbers in Knight Paths are known as 'Dawsonian' tours, sine they were originated by T. R. Dawson who showed a large number of them, including 100 showing symmetric circuits. Below we show a few examples where the squares are in an OPEN path of knight moves. Examples where the paths are CLOSED circuits are shown in Figured Tours - Part 2.
This famous problem set by G. E. Carpenter and solved by S. Hertzsprung in Brentano's Chess Monthly (May and Sep 1881) was to find a knight tour which when numbered along its path shows the eight square numbers aranged in sequence along a rank.

The square numbers can be regarded as following a straight wazir path.
An alternative set of solutions to the Carpenter problem were given by S. H. Hall (FCR 1937). In his 4th rank example the move-segments are successively above and below the line.

Others have given part solutions: G. Fuhlendorf (Fairy Chess Review 1937) on first rank, and A. S. M. Dickins (Chessics 1978) on fourth rank.

My own work in Chessics #22 1985 p.61 and in my article on 'Figured Tours' in Mathematical Spectrum (vol.25 1992/3 #1 p.16-20). Square numbers in square and rectangle.

From my booklet Figured Tours 1997 (a) closed wazir path in open knight tour. (b) symmetric open wazir path in closed knight tour. (c) square numbers in a C-shaped wazir path.

Here are three early examples by T. R. Dawson. He comments: "The apparently pointless 451 is given to emphasise the usefulness of Ciccolini's squares and diamonds in constructions of this kind - the whole tour being made up of these units, with squares in S-chain.". [In mis-attributing the squares and diamonds to Ciccolini he is following earlier authorities such as Lucas and Ahrens.] The tour is not strictly squares and diamonds since two moves are deleted from the top right diamond.

See also P. C. Taylor open tour with square numbers delineating D for Dawson.
From my 1997 Figured Tours booklet, two examples show symmetric open paths.

Three from P. C. Taylor's 1932 lecture but published in PFCS 1933, showing the square numbers in open Giraffe {1,4} chains.

Open tour with square numbers in a closed Giraffe circuit from Chessics #22 1985 p.61. Open tours with square numbers in closed Zebra {2,3} circuits from Figured Tours in Mathematical Spectrum (vol.25 1992/3 #1 p.16-20) and from Figured Tours booklet 1997.

Awani Kumar has supplied three PNG images showing the square numbers in Giraffe paths and one showing a Zebra path.

|

|

|
|
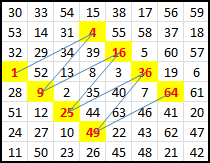
Awani Kumar has supplied these six PNG images showing square numbers in various longer leaper paths.
Two by antelope {3,4}, two by fiveleaper {3,4}+{0,5} and two by {2,5}-leaper.

|

|

|

|

|

|
And three more from Awani Kumar showing paths by even longer leapers. Two by (1,6) leaper and one by (3,6) which is a nightrider-type move.

|

|

|
Open tours by T. R. Dawson Comptes Rendus du Premier Congres International de Recreation Mathematique (CIRM 1935, two tours) and British Chess Magazine: (vol.63, 1943 p.23 ¶5970 sol p.70, one tour), and by G. P. Jelliss Figured Tours: A Mathematical Recreation (1997), with the square numbers occupying positions where 8 queens can be placed with none being in line, laterally or diagonally, with any other.

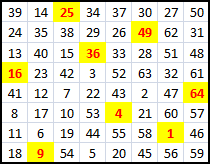
Awani Kumar has provided PNG images of eight solutions. A complete set for this problem.

|

|

|

|

|
|

|

|
Tours with the square numbers in a ring (Letter O) by S. H. Hall closed and T. R. Dawson open (PFCS 1935). TRD wrote: "I tried this same theme as long ago as July 1932".

Dennison Nixon Fairy Chess Review (vol.6 #4 Feb 1946 p.23 ¶6661-6663, sol. #5 Apr 1946 p.33). Put the square numbers on given cells to show letters T, R, D, and complete the tours.

The difficult R is unconvincing.
Closed tour by T. R. Dawson British Chess Magazine: 1941 with so-called 'pentagonal numbers' of form n·(3·n – 1)/2 in pentagon (1 d4, 5 e3, 12 b5, 22 f5, 35 c3, 51 d6).
Two tours by G.P. Jelliss, the first from Chessics #22 1985 p.61, an open tour with cubes in the corners, the second from Chessics #25 Spring 1986 p.106-7 a closed tour of squares and diamonds type, with so-called 'octagonal' numbers of form n·(3·n – 2) in the corners.

Six closed tours by T. R. Dawson in Comptes Rendus du Premier Congres International de Recreation Mathematique (CIRM 1935) with the ten triangular numbers 3, 6, 10, 15, 21, 28, 36, 45, 55 in triangular formations.

I also have a note of three in British Chess Magazine: (vol.60 1940) which are probably from this set.

The task of combining a path of squares with one of cubes was suggested by H. A. Adamson and the first example composed was this open tour by T. R. Dawson. He published a closed tour at the same time and another ten years later in BCM.

These three tours by Frans Hansson FCR 1938 have the cube path centred on the board.

My booklet Figured Tours 1997 included two examples with the squares and cubes each in symmetric open paths of knight moves, composed five years earlier.

T. R. Dawson (London) Evening Standard 1933. Tour with double triangle numbers n·(n+1) namely 2, 6, 12, 20, 30, 42, 56 in a figure of eight formation.
Mine is an asymmetric closed tour (Jeepyjay Diary Blog 26 Nov 2015) numbered 0 to 63 with the Metasquare Numbers n·(n+1) in cyclic order along a diagonal using n = 0 = 0·1 to make up a set of eight. A metasquare is the geometric mean of two successive squares.

T. R Dawson and S. H. Hall. Two tours with the eighteen odd primes in a rectangle, Dawson open, Hall closed (PFCS vol.2 #16 Feb 1936 p.172 ¶2179).

For further examples see the Prime Queen section below.
Following hints from the Rajah of Mysore I showed this tour in my 1997 booklet Figured Tours
with powers of two on the partial knight wheel round the initial cell, 1, which is 2^0.

From my Jeepyjay Diary online, a symmetric tour (9 Dec 2016) with the Legendre Numbers (4^k)·(8·n + 7) in the diagonals. These numbers are NOT the sum of three squares.

My article in Mathematical Spectrum (1992/3) included a symmetric open tour 9×9 with arithmetical progression with c.d. 10.

The open tour 9×9 with a starburst was set as a puzzle in my booklet on Figured Tours (1997).
When numbered from the centre it has even and odd numbers circling the centre cell.
The open figured tour on the 10×10 below was set as a puzzle in my booklet on Figured Tours (Jelliss 1997).
It has the arithmetic progression 1 to 100 with common difference 11 along a rank and the segments alternate in the lower and upper ranks.
This tour also shows approximate axial symmetry (only the three heavier moves in the centre deviate from symmetry).

For further 10×10 examples see the Prime Queen section below.
This open tour 11×11 was set as a puzzle in my booklet on Figured Tours (1997).
It shows the triangular numbers in a rectangle. Taken in sequence they follow a rook tour of alternating 2 and 1 steps.
Add 100 to the underlined numbers.

The dots in the symmetric tour (Jelliss 20 Apr 2019) represent the numbers 1, 13, 25, 37, 49, 61, 73, 85. 97, 109, 121
forming the arithmetic progression with common difference 12.

This is similar to the 5×5 and 7×7 and 9×9 figured tours shown in the previous sections,
but has the extra constraint that none of the linkage paths cross the diagonal.
Figured tours by the Rajah of Mysore on the 12×12 board. The ¶1 is an 8×8 with gnomon, numbered from f3,
and the numbers within a knight's move of the first cell (marked)
are: 2, 8, 24, 32, 16, 64, 72, 144 (multiples of 8, apart from 2).

And ¶10 numbered from f6 has the numbers 2, 18, 36, 54, 72, 90, 108, 144 a knight's move from 1
(includes 7 multiples of 18, the other, 126, is at b9).

For the frontispiece of the first issue in the second series of The Games and Puzzles Journal (vol.2 #13 May 1996 p.201)
I constructed this Figured tour on a 12×12 board with the Fibonacci numbers forming an oval (representing an Easter egg).
The same was used for the cover of my booklet Figured Tours: A Mathematical Recreation 1997.

The Dawsonian Tours web page Figured Tours - Part 2 includes further large board examples.
The following three Figured Knight's Tours are constructed so that a Queen placed on an appropriate cell guards all 17 odd primes; in other words the cells containing the odd prime numbers are all on the rank, file and diagonals through one particular cell. The first two solutions appeared on Mike Keith's fascinating "World of Words & Numbers" website, now replaced by his Cadaeic website where it is stated that the problem was first proposed by G. L. Honaker Jr. in November 1998.
The tours were also published in more colourful form in my Games and Puzzles Journal #19.
(A) by Mike Keith is an open tour showing all 18 primes (i.e. including the even prime 2) guarded by the queen on cell 35.
(B) by someone identified only as "gscgz" (April 1999) is a closed tour showing all 18 primes also guarded by the queen on cell 35.
(C) is a solution I found on 11 October 2000, and sent to Mike Keith, in which the queen, standing on square 1,
'observes' all 17 odd primes, and 'ignores' all 14 odd composite numbers.
(A) 37 24 45 04 39 22 47 62 44 05 38 23 46 61 40 21 25 36 43 60 03 20 63 48 06 59 26 35 64 41 02 19 27 30 57 42 01 34 49 12 58 07 54 29 52 13 18 15 31 28 09 56 33 16 11 50 08 55 32 53 10 51 14 17 |
(B) 19 58 33 06 21 16 13 08 32 05 20 17 34 07 22 15 57 18 59 04 29 14 09 12 42 31 56 35 62 11 28 23 55 60 43 30 03 24 63 10 44 41 46 61 36 27 50 25 47 54 39 02 49 52 37 64 40 45 48 53 38 01 26 51 |
(C) 15 12 19 64 23 10 07 04 20 63 14 11 18 05 24 09 13 16 61 22 01 08 03 06 62 21 50 17 60 37 30 25 51 46 53 42 29 02 59 36 54 43 40 49 38 33 26 31 47 52 45 56 41 28 35 58 44 55 48 39 34 57 32 27 |
Figure 5 11 48 15 06 21 24 27 08 16 05 12 47 10 07 22 25 49 14 03 20 23 26 09 28 04 17 40 II 46 29 42 61 30 50 19 02 41 62 45 30 18 53 36 57 32 43 60 63 51 38 55 34 01 58 31 44 54 35 52 37 56 33 64 59 |
Figure 6 13 48 15 96 21 24 27 08 16 05 12 47 10 07 22 25 49 14 03 20 23 26 09 28 04 17 40 II 46 29 42 59 39 50 19 02 41 58 45 30 18 53 36 57 32 43 60 63 51 38 55 34 01 62 31 44 54 35 52 37 56 33 64 61 |
Donald Knuth wrote 19 November 2022: My computer gave me a nice surprise this morning: It's a re-entrant 10×10 knight's tour in which each of the 25 primes is attacked by the queen labeled "45", with the additional nice property that: Every odd number attacked by the queen is either 1 or prime! Fun to watch the knight as it must get perked up whenever it comes into prime-rich territory, yet stay out of contact during a run of composite numbers. See above for the 8×8 examples that inspired this larger solution.
59 64 57 68 71 62 91 08 73 96 56 67 60 63 06 69 72 97 92 09 65 58 03 70 61 90 07 10 95 74 36 55 66 89 02 05 44 75 98 93 19 22 37 04 45 14 11 94 43 76 54 35 20 17 88 01 46 15 12 99 21 18 23 38 47 16 13 00 77 42 34 53 32 87 50 39 28 79 84 81 31 24 51 48 29 26 85 82 41 78 52 33 30 25 86 49 40 27 80 83 |
61 64 33 40 47 42 49 16 13 44 32 67 62 65 18 39 46 43 50 15 63 60 31 34 41 48 17 14 45 12 68 35 66 19 38 01 10 75 98 51 59 30 37 02 85 74 97 00 11 76 36 69 58 73 20 23 84 09 52 99 57 72 29 22 03 86 53 96 77 08 28 89 70 87 24 21 04 83 80 95 71 56 91 26 05 54 93 78 07 82 90 27 88 55 92 25 06 81 94 79 |
This puzzle was sent to me by Professor Donald E. Knuth on 24 November 2019.
I published it on Twitter on "Pi Day" March 14 2021 but obtained no response.
You are asked to complete a closed knight's tour, given the numbers shown,
which are the successive digits of pi.

|

|
Knuth records 228 solutions to this.
The diagram shown is the only one that has the number 21 on the cell d1,
which thus determines a complete tour.
This has been provided by the author in the form of a PDF, linked to above and here.
"Studies in Figured Tours of Knight in Two and Higher Dimensions" by Awani Kumar PDF: Kumar 2021.