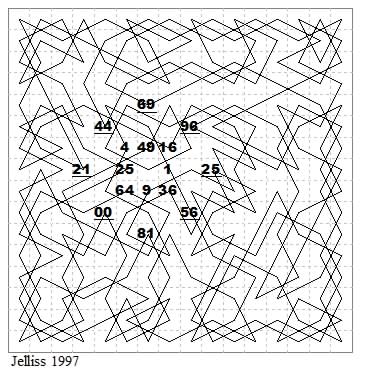
For an introduction to Figured Tours and their history see: Figured Tours - Part 1.
Sections on this page: — Dawsonian Tours
— Dawsonian Tours on the 6×6 Board
— Dawsonian Tours on the 8×8 Board
— Square Numbers in Axially Symmetric Circuits
— Square Numbers in Centro-Symmetric Circuits
— Dawsonian Tours by Other Composers
— Squares in Other Knight Paths
— Dawsonian Tours on Larger Boards.
T. R. Dawson invented the type of figured tour in which the square numbers form a knight chain. This was introduced in Problemist Fairy Chess Supplement (vol.1 #10 Feb 1932 ¶329 p.53, 58) and he seems to have shown examples to other members of the British Chess Problem Society before that date, since examples by P. C. Taylor were given in a lecture to the Society given in the same month on 26 Feb 1932 as mentioned in the British Chess Magazine (vol.52 1932 p182). This article contained a large number of knight's tours, either of the squares in a chain, or monogram types. Most of them were later published in PFCS/FCR over the years.
In the first article in PFCS Dawson stated: "No.329 is the first published solution of a question given by G. E. Carpenter in Brentano's, May 1881, to construct a knight tour with the square numbers in a knight chain." However, five years later (in FCR vol.3 #7 Aug 1937 p.77) he wrote: "The famous chess historian, H. J. R. Murray, a few months ago asked me to verify this reference, and to my astonishment it was quite incorrect — G. E. C. proposed no such problem. It appears that I must have unconsciously modified his actual proposition — S-tours with the integral square numbers all on one rank — into our present S-chain proposition. I now accept this child of my fantasy as my own, thanks to H. J. R. M." [S is the symbol used for Knight in PFCS/FCR.]
It only recently occurred to me to try the Dawson problem of a tour with the square numbers in a closed knight circuit on the 6×6 board. This work was published in my Jeepyjay Diary Blog from 14 Apr to 10 May 2017, where I found that four geometrically distinct circuits admit tours (one in two different potitions on the board).
It has been known for a long time (apparently in Chess Amateur though I've not located the exact reference) that there are 25 such geometrically distinct circuits. One is too large to fit on the 6×6 board. The others can be placed on the board in various positions (81 at my last count), and the numbers can be placed on them in up to 12 ways. However, many cases are easily eliminated. For instance in the first diagram below, the node at a5 must be an end-point (1 or 36) since there is only one other move available there.
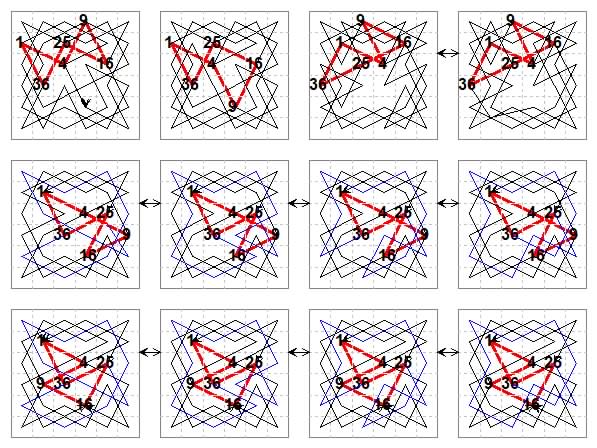
Awani Kumar examined this problem independently and reported in 2020 that he had found 12 solutions. I have redrawn the tours here {September 2022] to show all the variants, and with the link 1-4 oriented the same in each case for ease of comparison.

The first diagram shows the only solution found with a symmetric circuit. The tour around this and the second circuit can be completed in only the one way. The third circuit admits two tours (one of these was omitted from the count previously). The same circuit but in a different position on the board, and numbered from a different point allows four tours. The fourth circuit also admits four solutions. These differ only in the route taken from 25 to 36.
T. R. Dawson made a complete set of 100 tours with the square numbers in symmetric knight chains on this board, showing all possible eight-move symmetric circuits that will fit in a tour. They were published in PFCS/FCR over seventeen years 1932-1948. The 69 axial solutions were published 1932-1937, but the 31 other cases desultorily: 2 in 1932, 3 in 1938, 6 in 1944, 10 in 1945, 3 in 1946, 4 in 1947, 3 in 1948. It is of interest that, contrary to our terminology, he calls only the axial circuits 'symmetric' while the rotary circuits are 'pseudosymmetric'.
In PFCS (vol.2 #2 Aug 1933 p.4) he wrote: "The Knight's tour with the integral squares also in a S-chain continues to interest several members of our Fairy Ring and a number of examples have accumulated to enrich our collection in these pages" and (#3 Oct 1933 p.14): "I was asked recently why I printed so many of these tours. The answer is that I like them and like PFS to be a source of reference to a very complete collection of them."
In the following list I precede each tour by its angle coding, where 1 denotes the diagonal acute angle, 2 the lateral acute, 3 a right angle, 4 the lateral obtuse, 5 the diagonal obtuse and 6 the straight. These numbers indicate the nearest multiple of 30 degrees.
In PFCS vol.2 #10 Feb 1935 p.104 it is noted: "There is a pretty relationship, in the octagons formed by the integral square numbers, between those with orthogonal axes of symmetry and the closely similar shapes with diagonal axes of symmetry. Nos 493 and 492 are a good case in point, the orthogonal star of 493 being rotated 45 degrees into the diagonal star of 492." More precisely the angles transform 1«2 and 4«5 while 3 and 6 remain unchanged. [In his booklet Caissa's Wild Roses in Clusters (1937) Dawson calls this relationship 'modal transformation' and applies it more generally to chess problem themes.]
Some of the circuits can be described as 'self-dual', being unaltered by this transformation. In the following lists I give the self-dual cases first, then the modal pairs and finally those that have no dual. We gather the tours together here in two batches: those with reflective symmetry and those with rotational symmetry.
Dawson notes at the end of the collection (FCR #18 Jun 1948 p.138) that there are in fact 106 symmetric circuits, but 3 will not form part of a complete tour and 3 require a 9-rank board. These six shapes are modally related to each other in pairs. Their angle patterns are 15661566, 16561656, 15551656 which fit the 8×8 board and their duals are 24662466, 26462646, 24442646.
Among the axial solutions there are 4 that have three-unit lines, and 14 that have two-unit lines, and another 12 with two-unit lines among the rotary examples.
There are 69 axial solutions. Of these 5 are self-dual, 44 in dual pairs, and 20 non-dual.
There are three with skew axes of symmetry: These use only right (3) and straight (6) angles, so are self-dual.
There are 66 with lateral or diagonal axes, of which 4 are octonary (with 4 axes), four are quaternary (with 2 axes).
The remaining 58 have a single axis of symmetry. Among these there are 8 that have no cell on the axis, which Dawson calls a Virtual Axis (i.e. Sulian symmetry).
SELF-DUAL CASES (5)
No. 329 is the first published solution.
36363636 (square). 33663366 (rectangle), 33333636 (gnomon).

12121212 (eight point star). 45454545 (convex octagon):
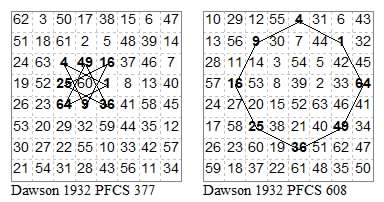
DUAL PAIRS. modally related (44 tours)
The first pair, like the star and octagon above, have four axes of symmerty.
14141414 (diagonal four-point star) 25252525 (lateral four-point star):

The next four have two axes of symmetry (both lateral or both diagonal).
34343434 and 35353535:
These can be regarded as the octagon with two opposite angles folded in.

23232323 and 13131313:
These can be regarded as the 8-star with two opposite angles folded out.

The remaining 19 dual pairs (38 tours) have a single axis of symmetry, lateral in one diagonal in the other. We show the simple circuits (without self-intersection) first (9 pairs).
22246264 and 11156165. These have successive two-move lines.
These can be regarded as diamonds with one acute angle folded in.

34345454, 35354545. Octagon with one angle folded in.

14143434, 25253535
Octagon with three angles folded in or 4-star with one angle folded out.

13231545, 13245423
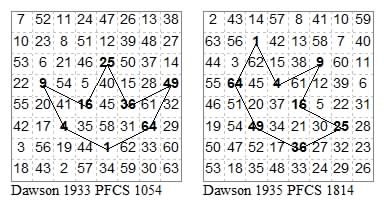
25354535, 14345434. Octago with adjacent angles folded in.
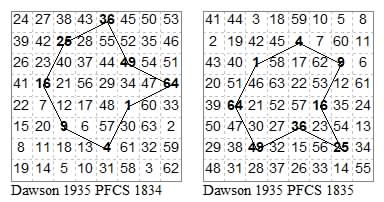
22223355 and 11113344 Can be seen as 4-stars with angle folded in.

11233334 and 12233335

14335334, 25334335

13345433, 23354533
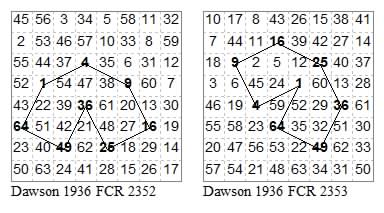
We now come to the dual pairs (10) that have self-intersection.
Six tours with single intersection.
14153235, 13425243
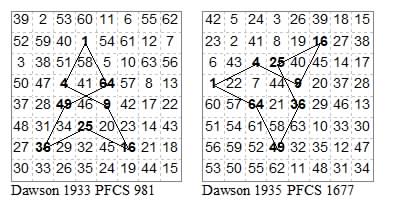
23534353 anf 13435343

23452345 and 13541354 virtual axis:
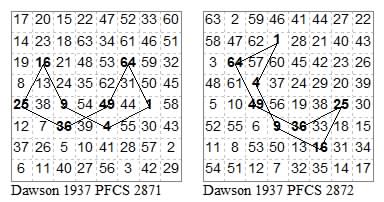
There is one pair with two self-intersections.
13431525, 14235324

Five pairs with triple intersection.
12335332, 12133433
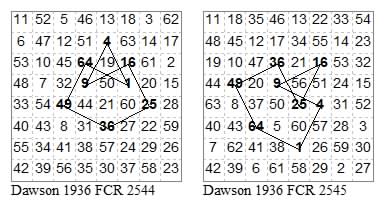
23314133, 13325233
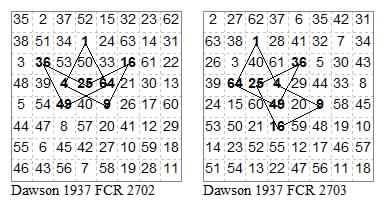
Tour 2703 above is of squares and diamonds except from 53 to 60. Many of the tours make use of squares and diamonds where possible.
12131413, 21232523

12153435, 21243534:
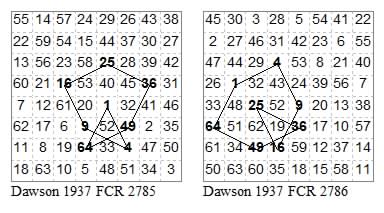
12341234 and 12531253 virtual axis.
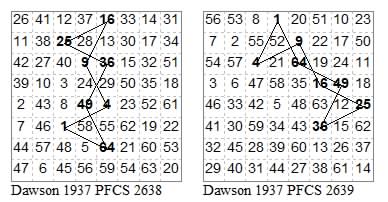
There is one pair with more than three self-intersections (in fact eight).
12123232, 12121313: Can be rgarded as 8-star with one angle folded out.
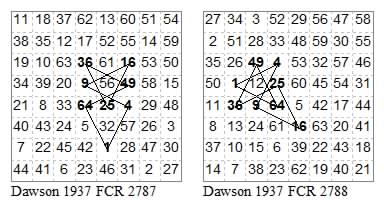
NON-DUAL CASES (20 circuits all with a diagonal axis of symmetry)
11231123, 23662366. Related 1«6, virtual axis.
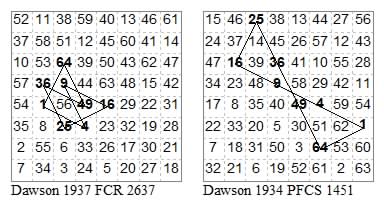
22612261, 33613361. Related 2«3, virtual axis.

Two with three-move lines
16635366, 16625266. Related 2«3, real axis.

Two with non-successive two-move lines
11163536, 11162526 . Related 2«3, real axis.

One cross-point
13261623, 13361633. Related 2«3, real axis.

Two cross-points
12521616, 13531616 . Related 2«3, real axis.

Three cross-points
12261622, 12361632 . Related 2«3, real axis.

11111353, 11111252 (comb patterns). Related 2«3, real axis.
One is a simple circuit but the other has four intersections.

11132123, 11123132. Related 2«3, real axis.
One has five intersections and the other seven.

For T. R. Dawson's example of this case see the section on Squares and Cubes - in Part 1. My version appeared in 'Further Notes on the Knight's Tour' (Chessics #25 Spring 1986 p.106) and has the chain of squares with its axis of symmetry along an axis of the board.
11133133, 11122122. Related 2«3, real axis.
One has a single intersection, the other has seven.

There are 31 centrosymmetric non-axial circuits that can be classified in various ways.
The 31 consist of 3 self-dual cases, 24 dual cases, and 4 without duals.
The 31 can also be classified as 16 centred at a point where four cells meet, 11 centred on a cell and 4 (those without duals) centred at the mid-point of the edge of a cell.
The 31 also consist of 19 simple circuits and 12 with self-intersection. There is one case of a dual pair where one is simple and the other is self-intersecting.
12541254 (= 21452145), 13261326 (= 23162316), 34653465 (= 35643564).

This is the only dual pair where both circuits are centred on a cell.
13531353, 23432343

In the following 8 pairs of modally related circuits (16 tours) one is centred at a point where four cells meet, but the other is centred at the centre of a cell.
14361436, 25362536

34563456, 35463546

13351335, 23342334
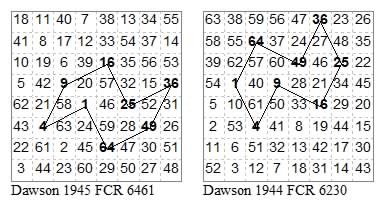
33553355, 33443344
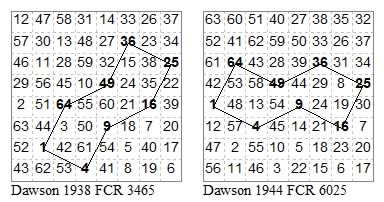
11331133, 22332233
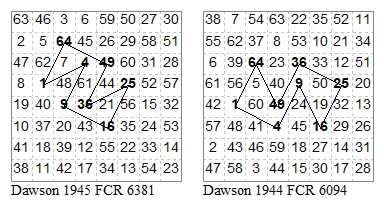
13641364, 23652365

12361236, 12631263
13351335, 23342334

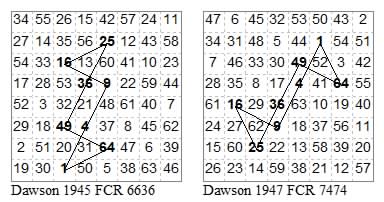
The following 3 pairs of duals (6 tours) are all centred where four cells meet.
14451445, 24552455

In the next case one circuit is self-intersecting but the other is simple.
13461346, 23562356

12251225, 11241124

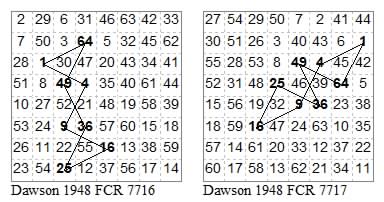
Finally four with centre at the mid-point of the edge of a cell (i.e. Bergholtian symmetry).
Two with one intersection: 25523443, 13313333.

Two with three intersections: 14412332, 15513113.
Dawson concluded: "These notes complete a 16-year piece of work -- nothing like sticking to it!"
In the earlier pages of PFCS other contributors also constructed examples of the tours with the square numbers in symmetric paths. These all differed from Dawson's own examples either in following different routes, being numbered from different points, or showing the circuit in a different position on the board.
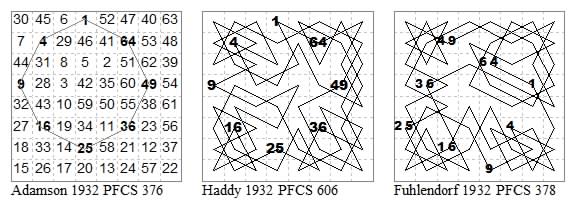
Octagons by H. A. Adamson and A. H. Haddy with varied routes. Square by G. Fuhlendorf. The latter two diagrams use an alternative style of presentation.
From his 1932 lecture P. C. Taylor shows squares in a chain: two symmetric circuits of the same rectangular shape and numbering but differently positioned. And one by A. H. Haddy.
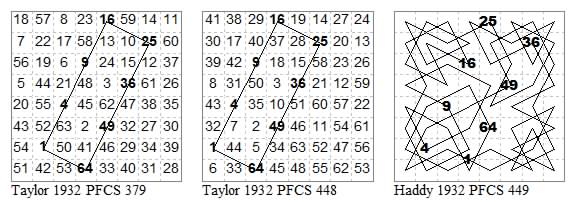
The two four-point stars by A. H. Haddy. The eight-point star by F. Dignal.
Acute angled gnomons by F. Dignal.

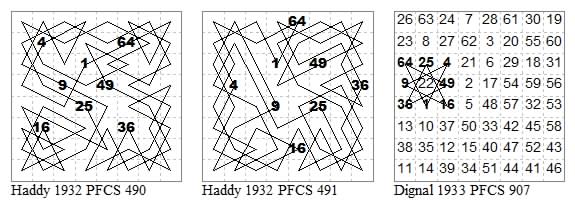
Three simple circuits by A. H. Haddy.
Self-intersecting examples by F. Dignal

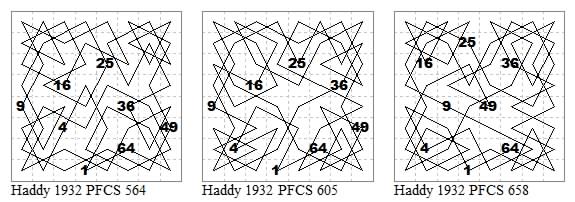
Two more Dawsonian symmetric closed simple circuits. Heart by A. H. Haddy. Rocket by F. Dignal.

Two more Dawsonian symmetric closed circuits. Crown by F. Dignal and Comb by A. H. Kniest, both from PFCS 1933.
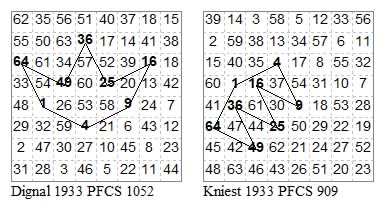
Asymmetric Dawsonian closed tour by A. H. Haddy with a matching example by Dawson.

In 'Further Notes on the Knight's Tour' (Chessics #25 Spring 1986 p.106-7). Closed tour with the squares in a knight path delineating a tour of the edges of a cube. This tour within a tour is one of my favourite results.

We conclude this section on closed tours with a remarkable symmetric tour with squares in knight chain by Valeriu Onitiu FCR 1939: "VO notes that he examined 144 dispositions of the squares, all that are possible for diametral symmetry, and this is the only case leading to a tour. Moreover every move of the tour is determined, so that the tour is UNIQUE in all the millions possible."

For much nmore on this subject see the new page Figured Tours - Part 3, where the Onitiu Problem is extended to larger boards and to cases with birotary symmetry.
This set of four Dawsonian tours on the 10×10 board show the four symmetric convex polygons that are possible. Two rectangles (1×4 and 2×3) and two ovals (hexagon and octagon).
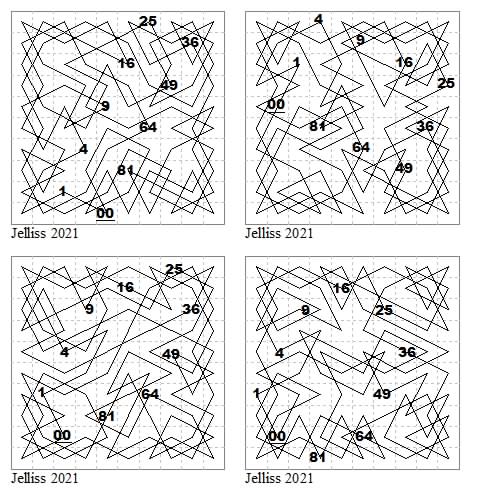
These were constructed 23-25 February 2021 and posted first in Twitter and then on my Jeepyjay Diary blog. Solving these configurations I find makes quite a good puzzle, probably a bit easier on the 10×10 board than the 8×8 because of the extra space.
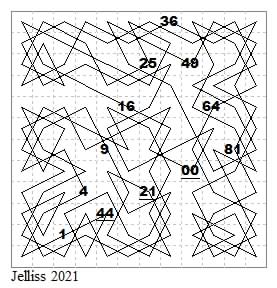
Dawsonian tour on the 12×12 board with the square numbers outlining a 3-4-5 triangle. Add 100 to underlined numbers.
The back page of my booklet on Figured Tours (1997) showed this 16×16 tour with the square numbers forming a tour of a hypercube (analogous to my 8×8 tour with the squares delineating a cube). Add 100 or 200 to underlined numbers.