Here we continue our study of knight's tours on oblong boards, that is rectangular boards that are not square. Following on from our studies of 3×n and 4×n tours, we consider boards having the smaller side greater than 5. Unlike those earlier studies however this section on larger boards is far less systematic, consisting mainly of a collection of somewhat arbitrary examples.
The only tours of oblong boards constructed during the mediaeval period were those on the 4×8 half-chessboard, in some cases two such tours being joined together to give a full-board tour. Tours of other oblong boards were first considered in Euler's seminal paper (1759). The next after Euler to study small boards was Willis (1821).
For closed tours of course the board must have an even number of cells. Some boards allow open tours but not closed tours. The obvious cases are rectangles odd by odd and boards 4×2n.
Closed Tours. On the 5×6 there are, surprisingly, only three closed tours, two of them having axial symmetry, these were found by Warnsdorf 1858 and Haldeman 1864, the other asymmetric tour found earlier by Euler 1759, combines the two halves of the symmetric tours.

If the central cells c3, d3 are omitted then there is a pseudotour of four circuits (two of 8 cells, two of 6 cells) on the remaining cells. The closed tours delete one move in each of these circuits and connect them with four new connections — two single links and two double links that pass through the central cells. Many of the open tours on this board are also of this form. Others split the circuits up.
Open Tours. There are no symmetric open tours on the 5×6 board. This is perhaps surprising, since a symmetric open tour is possible on the 3×4 board, which is the middle area of the 5×6 board. A graphical step by step proof is indicated. We try to construct a tour. The middle move must cross the centre point of the board and we can take it to be c4-d2. There are five ways it can be extended, as shown by the heavy lines in the first row. Cases 1, 2, 4, 5 imply a5,f1 are end cells and case 4 is immediately eliminated due to forming a 6-cell path.
In case 1 the moves through the other corners a1,f5 are fixed and also the moves through b1,e5. Then at b5,e1 the moves b5-d4, e1-c2 are forced since the other moves at b5,e1 form a 4-move circuit with those at b1,e5. Now at a3,f3 the moves to b5,e1 are the only moves available. At b2,e4 there are now three choices of move: b2-d3, e4-c3 give the 20-cell path shown at the top The other choices b2-a4, e4-f2 or b2-d1, e4-c5 give the diagrams in the first column. Moves at c5,d1 or at a4,f2 are now forced, giving 24-cell paths. Similar arguments apply in the other cases.
The maximum length paths are of 24 cells, and I find 24 solutions all shown below. The 6 unused cells form a cycle of moves round the border in every case. Cases 1 and 5 lead to four 24-cell paths, all the others are from case 3.

Here are some asymmetric open tours. The first from Willis (1821), then six from Kraitchik (1926), and two from Murray (1942) that show three two-move lines. The last (Jelliss 2015) approximates axial symmetry.

I find 288 symmetric open tours (U.Papa, 1920, claimed 260). Classified by separation of end-points they are: {0,2} 18 (4 horizontal c3-e3, and 14 vertical d2-d4); {0,6} 14 (all a3-g3); {2,4} 56 (12 horizontal, b2-g4 or b4-g2, and 44 vertical, c1-e5 or c5-e1); {4,6} 200 (a1-g5 or a5-g1). The corner-to-corner tours comprise much the larger class. They can be subclassified according to the direction of the straight line though the centre cell. If they are all drawn a5-g1 then the central two moves are b2-f4 (32 cases), b4-f2 (28 cases), c1-e5 (64 cases) or c5-e1 (76 cases). Examples of each case are shown. The first diagram is from Papa 1920, the second from Murray 1942, the third Jelliss 1985, the others Jelliss 1997.

Willis 1821 and Jaenisch 1862 gave asymmetric examples.

Murray (1942) writes: "The main interest in this board is that it can be used to build up tours on the chessboard by compartments. We [i.e. Murray, Bergholt and Moore] have found 11 tours in central diametral symmetry on this board." (Central diametral symmetry is Papa's term for bergholtian symmetry.) The 11 diagrams are then given. This agrees with my own enumeration, done independently in 1988. The first tour shown here is due to Bergholt, it is the only one in which the centre moves are cut four times. There are four in which they are cut twice, and in the remaining six they are not cut. The last of these was given by Papa (1922).

There are 22 reentrant symmetric open tour solutions (two from each of the 11 closed solutions). A few non-reentrant examples are shown.

Two example symmetric tours.

This board admits sulian, eulerian and bergholtian symmetry as well as asymmetry.

Four example symmetric tours, and two others by taking the alternative dashed routes:

For other examples of tri-directional tours see boards 3×4k, 6×9 and 7×7.
One example, a closed tour with bergholtian symmetry:
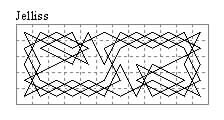
Two open symmetric examples (Jelliss 5 Feb 2023) with end separations {2,4} and {0,2}.

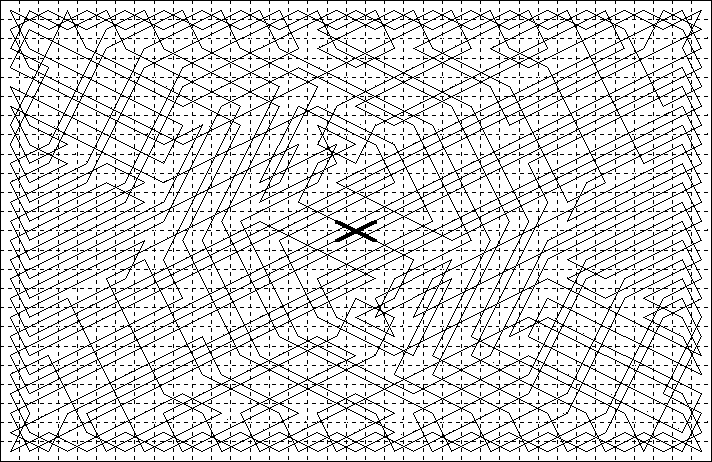
This tour of 100 cells (Jelliss 1988) was composed to mark the centenary of Australia: the central cross symbolising the Southern Cross.
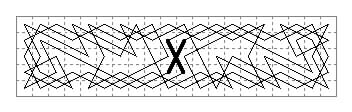
There are closed tours of all three symmetric types: Eulerian, Bergholtian and Sulian; seven of each are shown below.
The first to show examples of all three types was Bergholt. I find the patterns on this board particularly attractive and varied.
Asymmetry is also possible of course.
According to Professor Knuth the numbers of closed tours of the three symmetric types are:
Bergholtian 19, Eulerian 263, and Sulian 265, making 547 in all.
He also finds 266636 asymmetric, making 267183 geometrically distinct.
Thus the number of different diagrams (with the rectangle in a given orientation) amounts to 4×266636 + 2×547 = 1067638.
I think the 19 Bergholtian tours may have been known to Murray. My own enumeration confirmed this result.
However, in the case of Sulian tours I found 266, which were shown on the linked page in diagram form.
It took a long search recently to find the duplicate (it was found that 166 was a duplicate of 165).
A complete set of diagrams of the Bergholtian, Eulerian and Sulian tours are now [30 January 2023] available on the separate page:
6×7 symmetric tours.
They are shown there with the long side vertical, since this shows the axial symmetry of the Sulian tours more clearly.
Eulerian (the first is by Bergholt):

Bergholtian (the first is by Bergholt himself):

Sulian (the first is by Bergholt). The axis of symmetry in these is horizontal.
It is probably more natural for the human eye to perceive such symmetry if the axis is rotated to the vertical.

Asymmetry is also possible of course. This example is by Warnsdorf (Schachzeitung 1858):

I don't think the symmetric open tours have been counted. There are 38 reentrant solutions
(two from each of the 19 closed solutions of Bergholtian type). Here are a few non-reentrant examples:

Eulerian symmetry only. Tours by Haldeman, Bergholt and Jelliss (3).

6×8 Board: Semi-Magic Tours
Jean-Charles Meyrignac (26 August 2003) reports the following results: On the 6×8 board, my program found the 5 following tours (it only searched for tours beginning in a corner): [the ranks all add to 196]
1 36 23 38 7 30 47 14
22 39 6 31 46 15 8 29
35 2 37 24 9 28 13 48
40 21 32 5 16 45 10 27
3 34 19 42 25 12 17 44
20 41 4 33 18 43 26 11
-------------------------------
121 173 121 173 121 173 121 173
1 36 23 38 25 12 47 14
22 39 34 3 46 15 10 27
35 2 37 24 11 26 13 48
40 21 4 33 16 45 28 9
5 32 19 42 7 30 17 44
20 41 6 31 18 43 8 29
-------------------------------
123 171 123 171 123 171 123 171
1 20 43 30 11 18 41 32
44 29 2 19 42 31 12 17
21 4 27 48 13 10 33 40
28 45 24 3 34 37 16 9
5 22 47 26 7 14 39 36
46 25 6 23 38 35 8 15
-------------------------------
145 145 149 149 145 145 149 149
1 22 47 30 11 14 39 32
46 29 2 23 38 31 12 15
21 4 27 48 13 10 33 40
28 45 24 3 34 37 16 9
5 20 43 26 7 18 41 36
44 25 6 19 42 35 8 17
-------------------------------
145 145 149 149 145 145 149 149
1 8 45 38 17 10 47 30
44 39 2 9 46 29 16 11
3 24 7 18 37 48 31 28
40 43 36 25 6 19 12 15
23 4 41 34 21 14 27 32
42 35 22 5 26 33 20 13
-------------------------------
153 153 153 129 153 153 153 129
(total running time: 6 minutes)
Sulian examples by Murray and Jelliss. My example joins an asymmetric 3×9 open tour to a copy of itself.

Example tours by Murray and Jelliss.

6×12 Board: Semi-Magic Tours.
Here are two 6×12 examples constructed by joining together two of Awani Kumar's 6×6 semimagic tours, suitably chosen. The 6-cell lines add to 219 and the 12-cell lines to 510 and 366 (the magic constant would be 438).
26 39 24 31 28 53 8 57 6 13 10 71
37 32 27 52 23 30 55 14 9 70 5 12
40 25 38 29 54 51 58 7 56 11 72 69
33 36 47 20 43 22 15 18 65 2 61 4
48 41 34 45 50 19 66 59 16 63 68 1
35 46 49 42 21 44 17 64 67 60 3 62
26 39 24 43 52 41 56 69 66 13 10 71
37 44 27 40 23 54 67 14 57 70 65 12
28 25 38 53 42 51 58 55 68 11 72 9
45 36 47 32 19 22 15 6 17 2 61 64
48 29 34 21 50 31 18 59 4 63 8 1
35 46 49 30 33 20 5 16 7 60 3 62
Similar tours can be constructed by joining 6×6 semi-magic tours end-to-end to any length 6k.
Two examples, bergholtian symmetry. The first is from British Chess Magazine 1918.

Two examples.

Border method. On the 8×9 board the two concentric braids each consist of two equal strands (of 26 cells on the outer and 10 cells on the inner). So to join them by simple linking requires only four deletions and insertions, but the result is asymmetric as in the first diagram. The symmetric, bergholtian, tour in the second diagram uses six deletions.

Border method. On this board the two concentric braids each consist of four equal strands (of 14 cells on the outer and 6 cells on the inner). So to join them by simple linking requires eight deletions and insertions. The symmetric (Eulerian) tour here achieves this.

22 43 80 17 76 15 74 13 28 49 79 18 21 44 25 46 27 48 73 12 20 23 42 77 16 75 14 71 50 29 41 78 19 24 45 26 47 30 11 72 62 3 40 57 36 55 34 51 70 9 39 58 61 4 65 6 67 10 31 52 60 63 2 37 56 35 54 33 8 69 1 38 59 64 5 66 7 68 53 32 
|
22 43 80 17 76 45 26 15 74 47 79 18 21 44 25 16 75 46 27 14 20 23 42 77 50 71 12 29 48 73 41 78 19 24 11 30 49 72 13 28 62 3 40 57 70 51 32 9 68 53 39 58 61 4 31 10 69 52 33 8 60 63 2 37 56 65 6 35 54 67 1 38 59 64 5 36 55 66 7 34 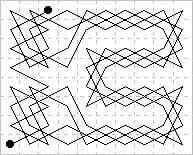
|
22 43 80 17 76 15 74 47 28 13 79 18 21 44 25 46 27 14 49 72 20 23 42 77 16 75 48 73 12 29 41 78 19 24 45 26 11 30 71 50 62 3 40 57 36 55 70 51 10 31 39 58 61 4 65 6 33 8 69 52 60 63 2 37 56 35 54 67 32 9 1 38 59 64 5 66 7 34 53 68 
|
The next example is constructed by the ‘lozenge’ method that I found for 12×12 magic tours, but due to the limitations of this board the result is only quasi-magic. The 10-cell lines add to 405 in five pairs adding to 81. The 8-cell lines add to 364 and 284 (the magic constant would be 324).
The final two examples, found among my notes and added here January 2013, have file totals 324. The rank totals are 445, 365 in one and 361, 449 innthe other.
65 70 67 60 63 18 21 14 11 16 68 57 64 19 22 59 62 17 24 13 71 66 69 58 61 20 23 12 15 10 56 29 6 73 54 27 8 75 52 25 5 72 55 28 7 74 53 26 9 76 30 35 32 3 38 41 80 49 46 51 33 4 37 42 79 2 39 44 77 48 36 31 34 1 40 43 79 47 50 45 
|
38 47 74 03 72 49 28 13 62 59 75 02 39 48 29 12 61 58 27 14 46 37 04 73 50 71 26 15 60 63 01 76 45 40 11 30 57 64 25 16 44 05 36 77 70 51 24 17 56 65 35 80 41 08 31 10 55 66 21 18 06 43 78 33 52 69 20 23 54 67 79 34 07 42 09 32 53 68 19 22 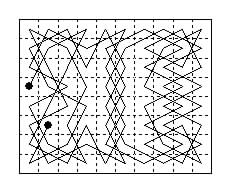
|
39 18 43 62 15 22 47 78 13 24 42 63 40 17 46 79 14 23 48 77 19 38 61 44 21 16 75 50 25 12 64 41 20 37 80 45 26 11 76 49 01 36 65 60 05 32 51 74 09 28 66 59 04 33 56 69 10 27 52 73 35 02 57 68 31 06 71 54 29 08 58 67 34 03 70 55 30 07 72 53 
|
The first four results above first appeared in The Games and Puzzles Journal, issue 26, April 2003.
Border method. On this board the number of strands in each braid reverts to two, as for the 8×9 board (but of 30 cells in the outer and 14 cells in the inner), so simple linking requires four deletions. The symmetric, bergholtian, tour here uses eight deletions.

The symmetric closed tour is by Murray 1942. The three open tour examples of near biaxial symmetry are by Victor Gorgias from the Dubuque Chess Journal 1871.

This example was constructed (by the lozenge method) 25 December 2012. The files add to 452 (formed of four pairs adding to 113 except in the 5th and 7th files where 1 - 3 and 59 - 57 are transposed). The ranks however add to four different totals 875, 707, (3 times each) and 819, 763 (once each).
36 47 70 73 34 109 52 89 32 107 12 15 94 105 71 74 35 46 51 58 33 108 27 90 95 106 11 14 48 37 72 69 110 53 112 29 88 31 16 13 104 93 75 64 45 50 59 111 54 87 30 85 22 17 92 103 65 76 41 44 1 60 3 84 25 82 97 100 9 20 42 39 78 67 62 55 80 5 86 23 18 7 102 99 77 66 43 40 79 4 61 24 81 6 101 98 19 8The structure consists of two central 3×8 areas containing the lozenges, with a 4×8 area added at right and left. For a magic rectangle of this size the rank sum should be 791 = 7×113.
These two new examples were constructed by splitting the 8×8 magic tour 00b in two and joining up the loose ends by four paths in direct quaternary symmetry.
42 31 110 107 26 47 128 87 24 85 22 53 134 83 74 7 66 143
111 108 43 30 129 88 25 48 127 54 133 84 21 52 65 142 75 6
32 41 106 109 46 27 130 55 86 23 126 51 62 135 8 73 144 67
105 112 29 44 117 100 89 14 49 132 95 20 9 64 141 68 5 76
40 33 116 101 28 45 56 131 96 13 50 125 136 81 72 77 140 1
113 104 39 36 99 118 15 90 59 122 19 94 63 10 137 4 69 78
34 37 102 115 16 57 120 97 18 91 12 61 124 93 80 71 2 139
103 114 35 38 119 98 17 58 121 60 123 92 11 62 3 138 79 70
42 31 110 107 26 53 98 123 126 55 58 11 128 83 74 7 66 143
111 108 43 30 99 124 25 54 97 12 127 84 57 10 65 142 75 6
32 41 106 109 52 27 96 125 122 59 56 13 82 129 8 73 144 67
105 112 29 44 117 100 51 24 95 14 85 130 9 64 141 68 5 76
40 33 116 101 28 45 94 121 50 131 60 15 136 81 72 77 140 1
113 104 39 36 93 118 49 20 23 86 89 132 63 16 137 4 69 78
34 37 102 115 46 21 120 91 48 133 18 61 88 135 80 71 2 139
103 114 35 38 119 92 47 22 19 90 87 134 17 62 3 138 79 70
Border method. The braids are formed of four equal strands (16 or 14 cells outer, 8 or 6 inner), so eight deletions are necessary for simple linking. The shorter circuits are symmetric, so for a symmetric tour two deletions must be made in each of these, making a minimum of 12 deletions; this is achieved in the example shown. There are two cells in the centre that also have to be joined into the tour, the two moves through these can be treated like a single insertion (Jelliss 1999).

Border method. There are two strands in the braids (48 and 24 outer, 16 and 8 inner) and three central cells to join in. Each strand is in direct quaternary symmetry. Asymmetric and symmetric examples by Jelliss 1999.

Border method. There are four strands in each braid (18 or 16 outer, 10 or 8 inner), two being centrosymmetric, and there are 2×3 central cells to be joined in. Thus twelve deletions at least for a symmetric tour. The example, bergholtian, uses 14 deletions, Jelliss 1999.

This tour by Pierre Dehornoy (2003) shows how to construct a tour with most of the knight's moves in two directions. The board can be expanded lengthwise in units of 12 and vertically in units of 6 by duplicating the edge and central components.

(Compare his 16×16 tour which has moves mainly in one direction.)
This tour (Jelliss 1985) which has oblique binary symmetry of bergholtian type, is constructed mainly in the form of a patchwork of areas each of which exhibits one of the eight possible patterns in which an area of board can be covered by straight lines of knight moves, one passing through each cell (see the note on translational symmetry on the Symmetry page). This was made by me for a Christmas/New Year card I sent out in 1985-6.